An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- My Bibliography
- Collections
- Citation manager

Save citation to file
Email citation, add to collections.
- Create a new collection
- Add to an existing collection
Add to My Bibliography
Your saved search, create a file for external citation management software, your rss feed.
- Search in PubMed
- Search in NLM Catalog
- Add to Search
Descriptive Statistics: Reporting the Answers to the 5 Basic Questions of Who, What, Why, When, Where, and a Sixth, So What?
Affiliation.
- 1 From the Department of Surgery and Perioperative Care, Dell Medical School at the University of Texas at Austin, Austin, Texas.
- PMID: 28891910
- DOI: 10.1213/ANE.0000000000002471
Descriptive statistics are specific methods basically used to calculate, describe, and summarize collected research data in a logical, meaningful, and efficient way. Descriptive statistics are reported numerically in the manuscript text and/or in its tables, or graphically in its figures. This basic statistical tutorial discusses a series of fundamental concepts about descriptive statistics and their reporting. The mean, median, and mode are 3 measures of the center or central tendency of a set of data. In addition to a measure of its central tendency (mean, median, or mode), another important characteristic of a research data set is its variability or dispersion (ie, spread). In simplest terms, variability is how much the individual recorded scores or observed values differ from one another. The range, standard deviation, and interquartile range are 3 measures of variability or dispersion. The standard deviation is typically reported for a mean, and the interquartile range for a median. Testing for statistical significance, along with calculating the observed treatment effect (or the strength of the association between an exposure and an outcome), and generating a corresponding confidence interval are 3 tools commonly used by researchers (and their collaborating biostatistician or epidemiologist) to validly make inferences and more generalized conclusions from their collected data and descriptive statistics. A number of journals, including Anesthesia & Analgesia, strongly encourage or require the reporting of pertinent confidence intervals. A confidence interval can be calculated for virtually any variable or outcome measure in an experimental, quasi-experimental, or observational research study design. Generally speaking, in a clinical trial, the confidence interval is the range of values within which the true treatment effect in the population likely resides. In an observational study, the confidence interval is the range of values within which the true strength of the association between the exposure and the outcome (eg, the risk ratio or odds ratio) in the population likely resides. There are many possible ways to graphically display or illustrate different types of data. While there is often latitude as to the choice of format, ultimately, the simplest and most comprehensible format is preferred. Common examples include a histogram, bar chart, line chart or line graph, pie chart, scatterplot, and box-and-whisker plot. Valid and reliable descriptive statistics can answer basic yet important questions about a research data set, namely: "Who, What, Why, When, Where, How, How Much?"
PubMed Disclaimer
Similar articles
- Fundamentals of Research Data and Variables: The Devil Is in the Details. Vetter TR. Vetter TR. Anesth Analg. 2017 Oct;125(4):1375-1380. doi: 10.1213/ANE.0000000000002370. Anesth Analg. 2017. PMID: 28787341 Review.
- Repeated Measures Designs and Analysis of Longitudinal Data: If at First You Do Not Succeed-Try, Try Again. Schober P, Vetter TR. Schober P, et al. Anesth Analg. 2018 Aug;127(2):569-575. doi: 10.1213/ANE.0000000000003511. Anesth Analg. 2018. PMID: 29905618 Free PMC article.
- Preparing for the first meeting with a statistician. De Muth JE. De Muth JE. Am J Health Syst Pharm. 2008 Dec 15;65(24):2358-66. doi: 10.2146/ajhp070007. Am J Health Syst Pharm. 2008. PMID: 19052282 Review.
- Summarizing and presenting numerical data. Pupovac V, Petrovecki M. Pupovac V, et al. Biochem Med (Zagreb). 2011;21(2):106-10. doi: 10.11613/bm.2011.018. Biochem Med (Zagreb). 2011. PMID: 22135849
- Introduction to biostatistics: Part 2, Descriptive statistics. Gaddis GM, Gaddis ML. Gaddis GM, et al. Ann Emerg Med. 1990 Mar;19(3):309-15. doi: 10.1016/s0196-0644(05)82052-9. Ann Emerg Med. 1990. PMID: 2310070
- Canadian midwives' perspectives on the clinical impacts of point of care ultrasound in obstetrical care: A concurrent mixed-methods study. Johnston BK, Darling EK, Malott A, Thomas L, Murray-Davis B. Johnston BK, et al. Heliyon. 2024 Mar 5;10(6):e27512. doi: 10.1016/j.heliyon.2024.e27512. eCollection 2024 Mar 30. Heliyon. 2024. PMID: 38533003 Free PMC article.
- Validation and psychometric testing of the Chinese version of the prenatal body image questionnaire. Wang Q, Lin J, Zheng Q, Kang L, Zhang X, Zhang K, Lin R, Lin R. Wang Q, et al. BMC Pregnancy Childbirth. 2024 Feb 1;24(1):102. doi: 10.1186/s12884-024-06281-w. BMC Pregnancy Childbirth. 2024. PMID: 38302902 Free PMC article.
- Cracking the code: uncovering the factors that drive COVID-19 standard operating procedures compliance among school management in Malaysia. Ahmad NS, Karuppiah K, Praveena SM, Ali NF, Ramdas M, Mohammad Yusof NAD. Ahmad NS, et al. Sci Rep. 2024 Jan 4;14(1):556. doi: 10.1038/s41598-023-49968-4. Sci Rep. 2024. PMID: 38177620 Free PMC article.
- Comparison of Nonneurological Structures at Risk During Anterior-to-Psoas Versus Transpsoas Surgical Approaches Using Abdominal CT Imaging From L1 to S1. Razzouk J, Ramos O, Harianja G, Carter M, Mehta S, Wycliffe N, Danisa O, Cheng W. Razzouk J, et al. Int J Spine Surg. 2023 Dec 26;17(6):809-815. doi: 10.14444/8542. Int J Spine Surg. 2023. PMID: 37748918 Free PMC article.
- CT-based analysis of oblique lateral interbody fusion from L1 to L5: location of incision, feasibility of safe corridor approach, and influencing factors. Razzouk J, Ramos O, Mehta S, Harianja G, Wycliffe N, Danisa O, Cheng W. Razzouk J, et al. Eur Spine J. 2023 Jun;32(6):1947-1952. doi: 10.1007/s00586-023-07555-1. Epub 2023 Apr 28. Eur Spine J. 2023. PMID: 37118479
- Search in MeSH
Related information
- Cited in Books
LinkOut - more resources
Full text sources.
- Ingenta plc
- Ovid Technologies, Inc.
- Wolters Kluwer
Other Literature Sources
- scite Smart Citations

- Citation Manager
NCBI Literature Resources
MeSH PMC Bookshelf Disclaimer
The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Descriptive Statistics | Definitions, Types, Examples
Published on July 9, 2020 by Pritha Bhandari . Revised on June 21, 2023.
Descriptive statistics summarize and organize characteristics of a data set. A data set is a collection of responses or observations from a sample or entire population.
In quantitative research , after collecting data, the first step of statistical analysis is to describe characteristics of the responses, such as the average of one variable (e.g., age), or the relation between two variables (e.g., age and creativity).
The next step is inferential statistics , which help you decide whether your data confirms or refutes your hypothesis and whether it is generalizable to a larger population.
Table of contents
Types of descriptive statistics, frequency distribution, measures of central tendency, measures of variability, univariate descriptive statistics, bivariate descriptive statistics, other interesting articles, frequently asked questions about descriptive statistics.
There are 3 main types of descriptive statistics:
- The distribution concerns the frequency of each value.
- The central tendency concerns the averages of the values.
- The variability or dispersion concerns how spread out the values are.

You can apply these to assess only one variable at a time, in univariate analysis, or to compare two or more, in bivariate and multivariate analysis.
- Go to a library
- Watch a movie at a theater
- Visit a national park
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
A data set is made up of a distribution of values, or scores. In tables or graphs, you can summarize the frequency of every possible value of a variable in numbers or percentages. This is called a frequency distribution .
- Simple frequency distribution table
- Grouped frequency distribution table
| Gender | Number |
|---|---|
| Male | 182 |
| Female | 235 |
| Other | 27 |
From this table, you can see that more women than men or people with another gender identity took part in the study. In a grouped frequency distribution, you can group numerical response values and add up the number of responses for each group. You can also convert each of these numbers to percentages.
| Library visits in the past year | Percent |
|---|---|
| 0–4 | 6% |
| 5–8 | 20% |
| 9–12 | 42% |
| 13–16 | 24% |
| 17+ | 8% |
Measures of central tendency estimate the center, or average, of a data set. The mean, median and mode are 3 ways of finding the average.
Here we will demonstrate how to calculate the mean, median, and mode using the first 6 responses of our survey.
The mean , or M , is the most commonly used method for finding the average.
To find the mean, simply add up all response values and divide the sum by the total number of responses. The total number of responses or observations is called N .
| Data set | 15, 3, 12, 0, 24, 3 |
|---|---|
| Sum of all values | 15 + 3 + 12 + 0 + 24 + 3 = 57 |
| Total number of responses | = 6 |
| Mean | Divide the sum of values by to find : 57/6 = |
The median is the value that’s exactly in the middle of a data set.
To find the median, order each response value from the smallest to the biggest. Then , the median is the number in the middle. If there are two numbers in the middle, find their mean.
| Ordered data set | 0, 3, 3, 12, 15, 24 |
|---|---|
| Middle numbers | 3, 12 |
| Median | Find the mean of the two middle numbers: (3 + 12)/2 = |
The mode is the simply the most popular or most frequent response value. A data set can have no mode, one mode, or more than one mode.
To find the mode, order your data set from lowest to highest and find the response that occurs most frequently.
| Ordered data set | 0, 3, 3, 12, 15, 24 |
|---|---|
| Mode | Find the most frequently occurring response: |
Measures of variability give you a sense of how spread out the response values are. The range, standard deviation and variance each reflect different aspects of spread.
The range gives you an idea of how far apart the most extreme response scores are. To find the range , simply subtract the lowest value from the highest value.
Standard deviation
The standard deviation ( s or SD ) is the average amount of variability in your dataset. It tells you, on average, how far each score lies from the mean. The larger the standard deviation, the more variable the data set is.
There are six steps for finding the standard deviation:
- List each score and find their mean.
- Subtract the mean from each score to get the deviation from the mean.
- Square each of these deviations.
- Add up all of the squared deviations.
- Divide the sum of the squared deviations by N – 1.
- Find the square root of the number you found.
| Raw data | Deviation from mean | Squared deviation |
|---|---|---|
| 15 | 15 – 9.5 = 5.5 | 30.25 |
| 3 | 3 – 9.5 = -6.5 | 42.25 |
| 12 | 12 – 9.5 = 2.5 | 6.25 |
| 0 | 0 – 9.5 = -9.5 | 90.25 |
| 24 | 24 – 9.5 = 14.5 | 210.25 |
| 3 | 3 – 9.5 = -6.5 | 42.25 |
| = 9.5 | Sum = 0 | Sum of squares = 421.5 |
Step 5: 421.5/5 = 84.3
Step 6: √84.3 = 9.18
The variance is the average of squared deviations from the mean. Variance reflects the degree of spread in the data set. The more spread the data, the larger the variance is in relation to the mean.
To find the variance, simply square the standard deviation. The symbol for variance is s 2 .
Prevent plagiarism. Run a free check.
Univariate descriptive statistics focus on only one variable at a time. It’s important to examine data from each variable separately using multiple measures of distribution, central tendency and spread. Programs like SPSS and Excel can be used to easily calculate these.
| Visits to the library | |
|---|---|
| 6 | |
| Mean | 9.5 |
| Median | 7.5 |
| Mode | 3 |
| Standard deviation | 9.18 |
| Variance | 84.3 |
| Range | 24 |
If you were to only consider the mean as a measure of central tendency, your impression of the “middle” of the data set can be skewed by outliers, unlike the median or mode.
Likewise, while the range is sensitive to outliers , you should also consider the standard deviation and variance to get easily comparable measures of spread.
If you’ve collected data on more than one variable, you can use bivariate or multivariate descriptive statistics to explore whether there are relationships between them.
In bivariate analysis, you simultaneously study the frequency and variability of two variables to see if they vary together. You can also compare the central tendency of the two variables before performing further statistical tests .
Multivariate analysis is the same as bivariate analysis but with more than two variables.
Contingency table
In a contingency table, each cell represents the intersection of two variables. Usually, an independent variable (e.g., gender) appears along the vertical axis and a dependent one appears along the horizontal axis (e.g., activities). You read “across” the table to see how the independent and dependent variables relate to each other.
| Number of visits to the library in the past year | |||||
|---|---|---|---|---|---|
| Group | 0–4 | 5–8 | 9–12 | 13–16 | 17+ |
| Children | 32 | 68 | 37 | 23 | 22 |
| Adults | 36 | 48 | 43 | 83 | 25 |
Interpreting a contingency table is easier when the raw data is converted to percentages. Percentages make each row comparable to the other by making it seem as if each group had only 100 observations or participants. When creating a percentage-based contingency table, you add the N for each independent variable on the end.
| Visits to the library in the past year (Percentages) | ||||||
|---|---|---|---|---|---|---|
| Group | 0–4 | 5–8 | 9–12 | 13–16 | 17+ | |
| Children | 18% | 37% | 20% | 13% | 12% | 182 |
| Adults | 15% | 20% | 18% | 35% | 11% | 235 |
From this table, it is more clear that similar proportions of children and adults go to the library over 17 times a year. Additionally, children most commonly went to the library between 5 and 8 times, while for adults, this number was between 13 and 16.
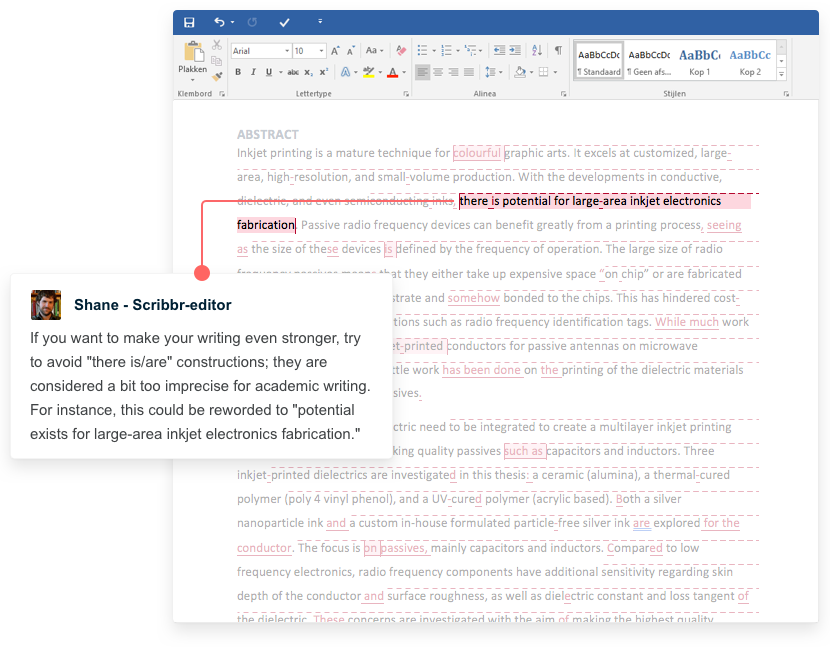
Scatter plots
A scatter plot is a chart that shows you the relationship between two or three variables . It’s a visual representation of the strength of a relationship.
In a scatter plot, you plot one variable along the x-axis and another one along the y-axis. Each data point is represented by a point in the chart.
From your scatter plot, you see that as the number of movies seen at movie theaters increases, the number of visits to the library decreases. Based on your visual assessment of a possible linear relationship, you perform further tests of correlation and regression.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Statistical power
- Pearson correlation
- Degrees of freedom
- Statistical significance
Methodology
- Cluster sampling
- Stratified sampling
- Focus group
- Systematic review
- Ethnography
- Double-Barreled Question
Research bias
- Implicit bias
- Publication bias
- Cognitive bias
- Placebo effect
- Pygmalion effect
- Hindsight bias
- Overconfidence bias
Descriptive statistics summarize the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalizable to the broader population.
The 3 main types of descriptive statistics concern the frequency distribution, central tendency, and variability of a dataset.
- Distribution refers to the frequencies of different responses.
- Measures of central tendency give you the average for each response.
- Measures of variability show you the spread or dispersion of your dataset.
- Univariate statistics summarize only one variable at a time.
- Bivariate statistics compare two variables .
- Multivariate statistics compare more than two variables .
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 21). Descriptive Statistics | Definitions, Types, Examples. Scribbr. Retrieved August 21, 2024, from https://www.scribbr.com/statistics/descriptive-statistics/
Is this article helpful?

Pritha Bhandari
Other students also liked, central tendency | understanding the mean, median & mode, variability | calculating range, iqr, variance, standard deviation, inferential statistics | an easy introduction & examples, what is your plagiarism score.

Quant Analysis 101: Descriptive Statistics
Everything You Need To Get Started (With Examples)
By: Derek Jansen (MBA) | Reviewers: Kerryn Warren (PhD) | October 2023
If you’re new to quantitative data analysis , one of the first terms you’re likely to hear being thrown around is descriptive statistics. In this post, we’ll unpack the basics of descriptive statistics, using straightforward language and loads of examples . So grab a cup of coffee and let’s crunch some numbers!
Overview: Descriptive Statistics
What are descriptive statistics.
- Descriptive vs inferential statistics
- Why the descriptives matter
- The “ Big 7 ” descriptive statistics
- Key takeaways
At the simplest level, descriptive statistics summarise and describe relatively basic but essential features of a quantitative dataset – for example, a set of survey responses. They provide a snapshot of the characteristics of your dataset and allow you to better understand, roughly, how the data are “shaped” (more on this later). For example, a descriptive statistic could include the proportion of males and females within a sample or the percentages of different age groups within a population.
Another common descriptive statistic is the humble average (which in statistics-talk is called the mean ). For example, if you undertook a survey and asked people to rate their satisfaction with a particular product on a scale of 1 to 10, you could then calculate the average rating. This is a very basic statistic, but as you can see, it gives you some idea of how this data point is shaped .

What about inferential statistics?
Now, you may have also heard the term inferential statistics being thrown around, and you’re probably wondering how that’s different from descriptive statistics. Simply put, descriptive statistics describe and summarise the sample itself , while inferential statistics use the data from a sample to make inferences or predictions about a population .
Put another way, descriptive statistics help you understand your dataset , while inferential statistics help you make broader statements about the population , based on what you observe within the sample. If you’re keen to learn more, we cover inferential stats in another post , or you can check out the explainer video below.
Why do descriptive statistics matter?
While descriptive statistics are relatively simple from a mathematical perspective, they play a very important role in any research project . All too often, students skim over the descriptives and run ahead to the seemingly more exciting inferential statistics, but this can be a costly mistake.
The reason for this is that descriptive statistics help you, as the researcher, comprehend the key characteristics of your sample without getting lost in vast amounts of raw data. In doing so, they provide a foundation for your quantitative analysis . Additionally, they enable you to quickly identify potential issues within your dataset – for example, suspicious outliers, missing responses and so on. Just as importantly, descriptive statistics inform the decision-making process when it comes to choosing which inferential statistics you’ll run, as each inferential test has specific requirements regarding the shape of the data.
Long story short, it’s essential that you take the time to dig into your descriptive statistics before looking at more “advanced” inferentials. It’s also worth noting that, depending on your research aims and questions, descriptive stats may be all that you need in any case . So, don’t discount the descriptives!

The “Big 7” descriptive statistics
With the what and why out of the way, let’s take a look at the most common descriptive statistics. Beyond the counts, proportions and percentages we mentioned earlier, we have what we call the “Big 7” descriptives. These can be divided into two categories – measures of central tendency and measures of dispersion.
Measures of central tendency
True to the name, measures of central tendency describe the centre or “middle section” of a dataset. In other words, they provide some indication of what a “typical” data point looks like within a given dataset. The three most common measures are:
The mean , which is the mathematical average of a set of numbers – in other words, the sum of all numbers divided by the count of all numbers.
The median , which is the middlemost number in a set of numbers, when those numbers are ordered from lowest to highest.
The mode , which is the most frequently occurring number in a set of numbers (in any order). Naturally, a dataset can have one mode, no mode (no number occurs more than once) or multiple modes.
To make this a little more tangible, let’s look at a sample dataset, along with the corresponding mean, median and mode. This dataset reflects the service ratings (on a scale of 1 – 10) from 15 customers.

As you can see, the mean of 5.8 is the average rating across all 15 customers. Meanwhile, 6 is the median . In other words, if you were to list all the responses in order from low to high, Customer 8 would be in the middle (with their service rating being 6). Lastly, the number 5 is the most frequent rating (appearing 3 times), making it the mode.
Together, these three descriptive statistics give us a quick overview of how these customers feel about the service levels at this business. In other words, most customers feel rather lukewarm and there’s certainly room for improvement. From a more statistical perspective, this also means that the data tend to cluster around the 5-6 mark , since the mean and the median are fairly close to each other.
To take this a step further, let’s look at the frequency distribution of the responses . In other words, let’s count how many times each rating was received, and then plot these counts onto a bar chart.
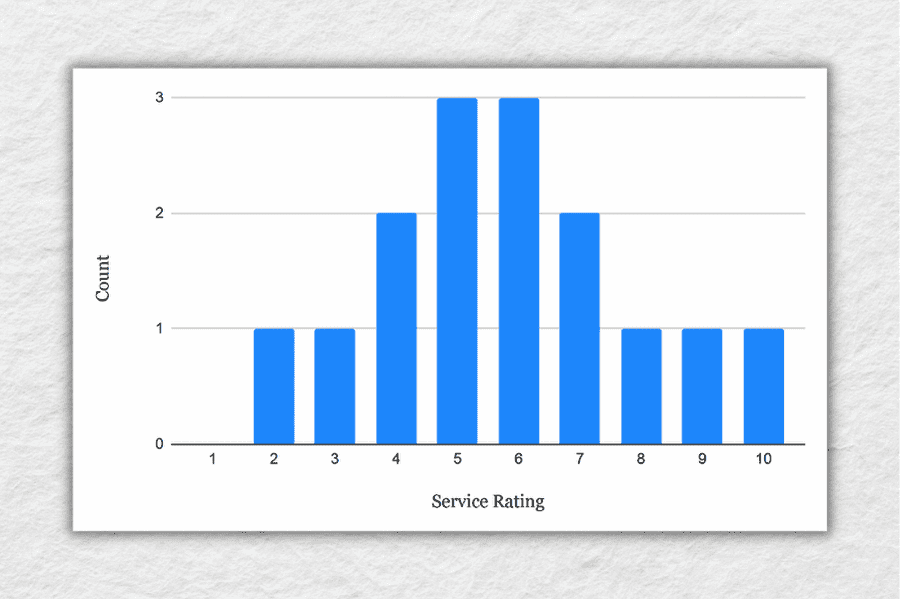
As you can see, the responses tend to cluster toward the centre of the chart , creating something of a bell-shaped curve. In statistical terms, this is called a normal distribution .
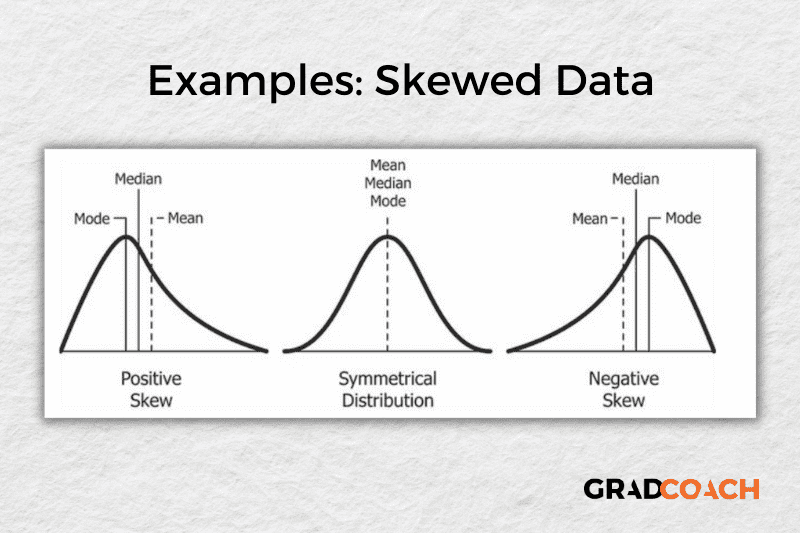
As you delve into quantitative data analysis, you’ll find that normal distributions are very common , but they’re certainly not the only type of distribution. In some cases, the data can lean toward the left or the right of the chart (i.e., toward the low end or high end). This lean is reflected by a measure called skewness , and it’s important to pay attention to this when you’re analysing your data, as this will have an impact on what types of inferential statistics you can use on your dataset.
Measures of dispersion
While the measures of central tendency provide insight into how “centred” the dataset is, it’s also important to understand how dispersed that dataset is . In other words, to what extent the data cluster toward the centre – specifically, the mean. In some cases, the majority of the data points will sit very close to the centre, while in other cases, they’ll be scattered all over the place. Enter the measures of dispersion, of which there are three:
Range , which measures the difference between the largest and smallest number in the dataset. In other words, it indicates how spread out the dataset really is.
Variance , which measures how much each number in a dataset varies from the mean (average). More technically, it calculates the average of the squared differences between each number and the mean. A higher variance indicates that the data points are more spread out , while a lower variance suggests that the data points are closer to the mean.
Standard deviation , which is the square root of the variance . It serves the same purposes as the variance, but is a bit easier to interpret as it presents a figure that is in the same unit as the original data . You’ll typically present this statistic alongside the means when describing the data in your research.
Again, let’s look at our sample dataset to make this all a little more tangible.
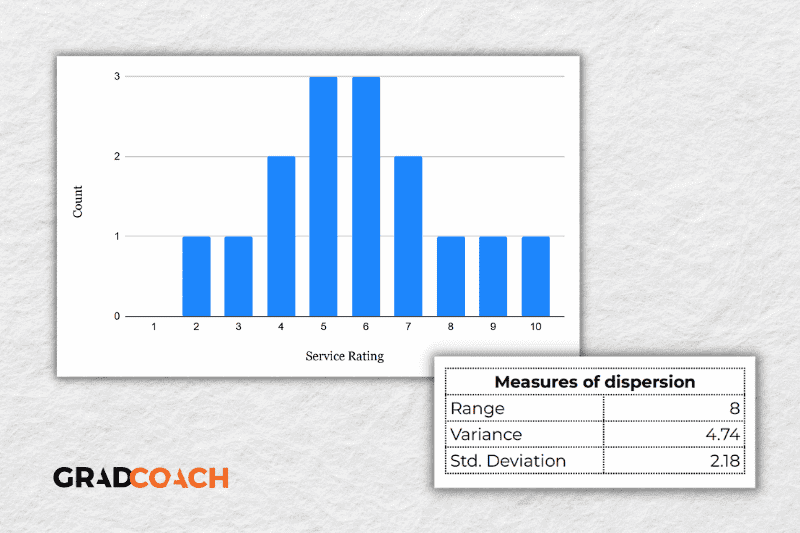
As you can see, the range of 8 reflects the difference between the highest rating (10) and the lowest rating (2). The standard deviation of 2.18 tells us that on average, results within the dataset are 2.18 away from the mean (of 5.8), reflecting a relatively dispersed set of data .
For the sake of comparison, let’s look at another much more tightly grouped (less dispersed) dataset.
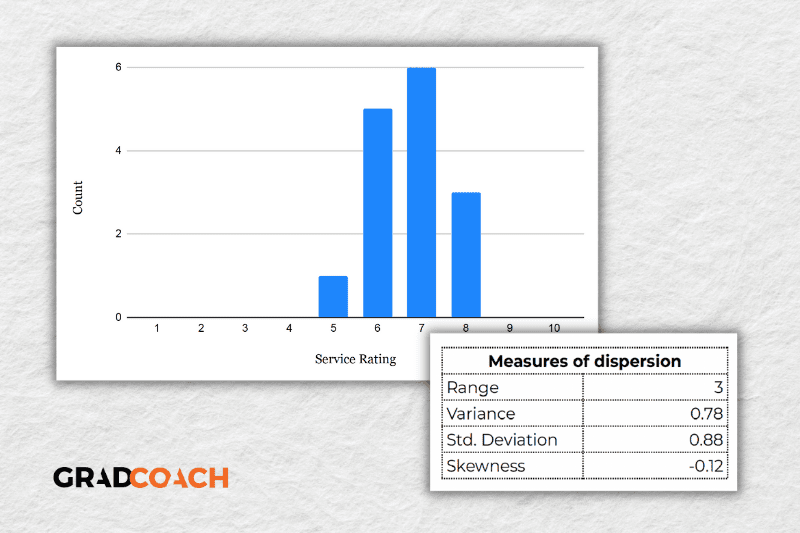
As you can see, all the ratings lay between 5 and 8 in this dataset, resulting in a much smaller range, variance and standard deviation . You might also notice that the data are clustered toward the right side of the graph – in other words, the data are skewed. If we calculate the skewness for this dataset, we get a result of -0.12, confirming this right lean.
In summary, range, variance and standard deviation all provide an indication of how dispersed the data are . These measures are important because they help you interpret the measures of central tendency within context . In other words, if your measures of dispersion are all fairly high numbers, you need to interpret your measures of central tendency with some caution , as the results are not particularly centred. Conversely, if the data are all tightly grouped around the mean (i.e., low dispersion), the mean becomes a much more “meaningful” statistic).
Key Takeaways
We’ve covered quite a bit of ground in this post. Here are the key takeaways:
- Descriptive statistics, although relatively simple, are a critically important part of any quantitative data analysis.
- Measures of central tendency include the mean (average), median and mode.
- Skewness indicates whether a dataset leans to one side or another
- Measures of dispersion include the range, variance and standard deviation
If you’d like hands-on help with your descriptive statistics (or any other aspect of your research project), check out our private coaching service , where we hold your hand through each step of the research journey.

Psst… there’s more!
This post is an extract from our bestselling short course, Methodology Bootcamp . If you want to work smart, you don't want to miss this .
Good day. May I ask about where I would be able to find the statistics cheat sheet?
Right above you comment 🙂
Good job. you saved me
Brilliant and well explained. So much information explained clearly!
Submit a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Print Friendly
- Search Menu
- Sign in through your institution
- Ageing - Other
- Bladder and Bowel Health
- Cardiovascular
- Community Geriatrics
- Dementia and Related Disorders
- End of Life Care
- Ethics and Law
- Falls and Bone Health
- Frailty in Urgent Care Settings
- Gastroenterology and Clinical Nutrition
- Movement Disorders
- Perioperative Care of Older People Undergoing Surgery
- Pharmacology and therapeutics
- Respiratory
- Sarcopenia and Frailty Research
- Telemedicine
- Advance articles
- Editor's Choice
- Supplements
- Themed collections
- The Dhole Eddlestone Memorial Prize
- 50th Anniversary Collection
- Author Guidelines
- Submission Site
- Open Access
- Reasons to Publish
- Advertising and Corporate Services
- Journals Career Network
- Advertising
- Reprints and ePrints
- Sponsored Supplements
- Branded Books
- About Age and Ageing
- About the British Geriatrics Society
- Editorial Board
- Self-Archiving Policy
- Journals on Oxford Academic
- Books on Oxford Academic

Article Contents
Introduction, describing the distribution of values, descriptive statistics in text, descriptive statistics in tables, describing loss of participants in a study, comparing baseline characteristics in rcts, conclusions, acknowledgements, conflicts of interest.
- < Previous
Describing the participants in a study
- Article contents
- Figures & tables
- Supplementary Data
R. M. Pickering, Describing the participants in a study, Age and Ageing , Volume 46, Issue 4, July 2017, Pages 576–581, https://doi.org/10.1093/ageing/afx054
- Permissions Icon Permissions
This paper reviews the use of descriptive statistics to describe the participants included in a study. It discusses the practicalities of incorporating statistics in papers for publication in Age and Aging , concisely and in ways that are easy for readers to understand and interpret.
Most papers reporting analysis of clinical data will at some point use statistics to describe the socio-demographic characteristics and medical history of the study participants. An important reason for doing this is to give the reader some idea of the extent to which study findings can be generalised to their own local situation. The production of descriptive statistics is a straightforward matter, most statistical packages producing all the statistics one could possibly desire, and a choice has to be made over which ones to present. These then have to be included in a paper in a manner that is easy for readers to assimilate. There may be constraints on the amount of space available, and it is in any case a good idea to make statistical display as concise as possible. This article reviews the statistics that might be used to describe a sample of older people, and gives tips on how best to do this in a paper for publication in Age and Aging . It builds on a previously published paper [ 1 ].
The values observed in a group of subjects, when measurements of a quantitative characteristic are made, are called the distribution of values. Graphical displays can be used to show the detail of the distribution in a variety of ways, but they take up a considerable amount of space. A precis of two key features of the distribution, its centre and its spread, is usually presented using descriptive statistics. The centre of a distribution can be described by its mean or median, and the spread by its standard deviation (SD), range, or inter-quartile range (IQR). Definitions and properties of these statistics are given in statistical textbooks [ 2 ].
Figure 1 a shows an idealised symmetric distribution for a quantitative variable. The mean might be used here to describe where the centre of the distribution lies and the SD to give an idea of how spread out values are around the centre. SDs are particularly appropriate where a symmetric distribution approximately follows the bell-shaped pattern shown in Figure 1 a which is called the normal distribution. For such a distribution the large majority, 95%, of values observed in a sample will fall between the values two SDs above and below the mean, called the normal range. Presentation of the mean and SD invites the reader to calculate the normal range and think of it as covering most of the distribution of values. Another reason for presenting the SD is that it is required in calculations of sample size for approximately normally distributed outcomes, and can be used by readers in planning future studies. A graphical display of approximately normally distributed real data (age at admission amongst 373 study participants) is shown in Figure 1 c: with relatively small sample size a smooth distribution such as that shown in Figure 1 a cannot be achieved. The mean (82.9) and SD (6.8) of the age distribution lead to the normal range 69.3–96.5 years, which can be seen in Figure 1 c to cover most of the ages in the sample: 14 subjects fall below 69.3 and 7 fall above 96.5, so that the range actually covers 352 (94.4%) of the 373 participants, close to the anticipated 95%. For familiar measurements, such as age, there is additional value in presenting the range, the minimum and maximum values attained. Knowing that the study included people aged between 65 and 101 years is immediately meaningful, whereas the value of the SD is more difficult to interpret.

Idealised and real data distributions. (a) Symmetrical distribution. (b) Skewed distribution. (c) Dotplot (each dot representing one value) of an approximate symmetrical distribution indicating the normal range: age in years at admission ( n = 373). (d) Dotplot (each dot representing one value) of a skewed distribution with outliers emphasised and indicating mean and median: hours in A&E ( n = 348).
When a distribution is skewed (Figure 1 b) just one or two extreme values, ‘outliers’, in one of the tails of the distribution (to the right in Figure 1 b) pull the mean away from the obvious central value. An alternative statistic describing central location is the median, defined as the point with 50% of the sample falling above it and 50% below. Figure 1 d shows the distribution of real data (hours in A&E amongst 348 study participants) following a skewed distribution. A few excessively long A&E stays pull the mean to the higher value of 4.9 h compared to the median of 4.4 h: the effect would be greater with a higher proportion of subjects having long stays. The median is often recommended as the preferred statistic to describe the centre of a skewed distribution, but the mean can be helpful. If the attribute being described takes only a limited number of values, the medians of two groups can take the same value in spite of substantial differences in the tails. In these circumstances, the mean can be sensitive to an overall shift in distribution while the median is not. When a comparison of cost based on length of stay is to be made, presenting means of the skewed distributions facilitates calculation of cost savings per subject by applying unit cost to the difference in means. Figure 1 b suggests that the value with highest frequency might be a useful descriptor of the centre of a distribution. In practice, this can prove awkward: depending on the precision of measurement there may be no value occurring more than once.
It is clear from Figure 1 b that no single number can adequately describe the spread of a skewed distribution because spread is greater in one direction than the other. The range (from 1.7 to 40.3 h in A&E in our skewed example) could be used. Another possibility is the IQR (from 3.5 to 5.4 h in A&E) covering the central 50% of the distribution. The SD may be presented even though a distribution is skewed, and could be useful to readers for approximate power calculations, but the normal range derived from the mean and SD will be misleading. With mean(SD) = 4.9(3.2), the lower limit of the normal range of hours in A&E is the impossible negative value of –1.5 h, while the upper limit of 11.3 h lies well below the extreme values exhibited in Figure 1 d.
Descriptive statistics may be presented in text, for example [ 3 ]:
Participants’ ages ranged from 50 to 87 years ( M = 66.1, SD = 7.8) with 56% identified as female, 64% married or partnered, 23% reported being retired or not working, 55% had post-secondary and higher education, and <20% reported living alone. Over 60% of the participants identified as NZ European. The mean of net personal annual income was $34,615. The participants reported the diagnosis of an average of 2.63 (±2.07) chronic health conditions, with 50% reported having three or more chronic health conditions.
There are perhaps too many attributes (age, gender, marital status, employment status, educational level, living arrangements, nationality, personal income and number of chronic conditions) being described in the excerpt above: it would be easier to assimilate this information from a table.
Characteristics of subjects at admission and their operations before (1998/99) and after (2000/01) implementation of a care pathway [ 4 ]. Figures are number (% of non-missing values) unless otherwise stated
| . | 1998/99 ( = 395) . | 2000/01 ( = 373) . |
|---|---|---|
| Age on admission (years) | ||
| Mean (SD) | 83 (7) | 83 (7) |
| Minimum–maximum | 65–101 | 65–101 |
| Gender | ||
| Male | 90 (23%) | 90 (24%) |
| Female | 305 (77%) | 283 (76%) |
| Admission domicile | ||
| Own home | 219 (55%) | 202 (54%) |
| Sheltered accommodation | 47 (12%) | 58 (16%) |
| Residential care | 90 (23%) | 83 (22%) |
| Nursing home | 18 (5%) | 15 (4%) |
| Other ward SUHT | 7 (2%) | 2 (1%) |
| Other trust | 14 (4%) | 13 (4%) |
| Ambulation score | ||
| Bed/chair bound | 8 (2%) | 5 (1%) |
| Presence 1+ | 12 (3%) | 7 (2%) |
| 1 person | 25 (6%) | 20 (5%) |
| Unable 50 m | 145 (37%) | 138 (38%) |
| Able 50 m | 200 (51%) | 197 (54%) |
| ( = 390) | ( = 367) | |
| Time in A&E (h) | ||
| Mean (SD) | 4.9 (3.2) | 5.6 (2.4) |
| Minimum–maximum | 1.7–40.3 | 0–21.4 |
| ( = 348) | ( = 328) | |
| History of dementia | 79 (20%) | 85 (23%) |
| ( = 395) | ( = 371) | |
| Confused on admission | 124 (32%) | 125 (34%) |
| ( = 394) | ( = 371) | |
| Type of fracture | ||
| Intra-capsular | 192 (54%) | 173 (52%) |
| Extra-capsular | 165 (46%) | 161 (48%) |
| ( = 357) | ( = 334) | |
| Operation more than 48 h after ward admission | 183 (52%) | 205 (64%) |
| ( = 354) | ( = 323) | |
| Reason for delayed operation | ||
| Medical | 61 (35%) | 74 (43%) |
| Organisational | 66 (38%) | 72 (42%) |
| Both | 45 (26%) | 27 (16%) |
| ( = 172) | ( = 173) | |
| Type of operation | ||
| Thompson's hemiarthroplasty | 101 (27%) | 87 (24%) |
| Austin-Moore hemiarthroplasty | 69 (19%) | 18 (5%) |
| Dynamic screw | 162 (43%) | 165 (46%) |
| Asnis screws | 38 (11%) | 38 (11%) |
| Bipolar hemiarthroplasty | 3 (1%) | 48 (14%) |
| ( = 373) | ( = 356) | |
| Grade of surgeon | ||
| Consultant | 46 (12%) | 110 (32%) |
| SPR | 318 (86%) | 220 (63%) |
| SHO | 6 (2%) | 18 (5%) |
| ( = 355) | ( = 348) | |
| Grade of anaesthetist | ||
| Consultant | 1206 (34%) | 175 (55%) |
| SPR | 99 (28%) | 52 (16%) |
| SHO | 133 (38%) | 81 (29%) |
| ( = 352) | ( = 318) | |
| . | 1998/99 ( = 395) . | 2000/01 ( = 373) . |
|---|---|---|
| Age on admission (years) | ||
| Mean (SD) | 83 (7) | 83 (7) |
| Minimum–maximum | 65–101 | 65–101 |
| Gender | ||
| Male | 90 (23%) | 90 (24%) |
| Female | 305 (77%) | 283 (76%) |
| Admission domicile | ||
| Own home | 219 (55%) | 202 (54%) |
| Sheltered accommodation | 47 (12%) | 58 (16%) |
| Residential care | 90 (23%) | 83 (22%) |
| Nursing home | 18 (5%) | 15 (4%) |
| Other ward SUHT | 7 (2%) | 2 (1%) |
| Other trust | 14 (4%) | 13 (4%) |
| Ambulation score | ||
| Bed/chair bound | 8 (2%) | 5 (1%) |
| Presence 1+ | 12 (3%) | 7 (2%) |
| 1 person | 25 (6%) | 20 (5%) |
| Unable 50 m | 145 (37%) | 138 (38%) |
| Able 50 m | 200 (51%) | 197 (54%) |
| ( = 390) | ( = 367) | |
| Time in A&E (h) | ||
| Mean (SD) | 4.9 (3.2) | 5.6 (2.4) |
| Minimum–maximum | 1.7–40.3 | 0–21.4 |
| ( = 348) | ( = 328) | |
| History of dementia | 79 (20%) | 85 (23%) |
| ( = 395) | ( = 371) | |
| Confused on admission | 124 (32%) | 125 (34%) |
| ( = 394) | ( = 371) | |
| Type of fracture | ||
| Intra-capsular | 192 (54%) | 173 (52%) |
| Extra-capsular | 165 (46%) | 161 (48%) |
| ( = 357) | ( = 334) | |
| Operation more than 48 h after ward admission | 183 (52%) | 205 (64%) |
| ( = 354) | ( = 323) | |
| Reason for delayed operation | ||
| Medical | 61 (35%) | 74 (43%) |
| Organisational | 66 (38%) | 72 (42%) |
| Both | 45 (26%) | 27 (16%) |
| ( = 172) | ( = 173) | |
| Type of operation | ||
| Thompson's hemiarthroplasty | 101 (27%) | 87 (24%) |
| Austin-Moore hemiarthroplasty | 69 (19%) | 18 (5%) |
| Dynamic screw | 162 (43%) | 165 (46%) |
| Asnis screws | 38 (11%) | 38 (11%) |
| Bipolar hemiarthroplasty | 3 (1%) | 48 (14%) |
| ( = 373) | ( = 356) | |
| Grade of surgeon | ||
| Consultant | 46 (12%) | 110 (32%) |
| SPR | 318 (86%) | 220 (63%) |
| SHO | 6 (2%) | 18 (5%) |
| ( = 355) | ( = 348) | |
| Grade of anaesthetist | ||
| Consultant | 1206 (34%) | 175 (55%) |
| SPR | 99 (28%) | 52 (16%) |
| SHO | 133 (38%) | 81 (29%) |
| ( = 352) | ( = 318) | |
The distributions of the two quantitative variables in Table 1 are described by mean (SD) and range. The statistics being presented should be stated in the context of the table, here in the left hand column, and could differ across variables. If the same statistics are presented for all the variables in a table they can be indicated in the column headings or title. From the mean (SD) and range in each phase, we can see that the age distribution is reasonably symmetrical because the mean falls close to the centre of the range, and the mean ± 2 SD approach the limits of the range. The distribution of hours in A&E is skewed to the right but has been summarised with the same statistics. We can see that the distribution is skewed because the mean is much closer to the minimum than the maximum, and, if the normal range is calculated, the upper limit does not approach the high values in either phase. For these reasons, the normal range should not be interpreted as covering 95% of values. These conclusions from descriptive statistics alone can be verified in Figure 1 c and d.
A choice arises when describing the distribution of an ordinal variable indicating ordered response categories, such as ambulation score in Table 1 . If the variable takes many distinct values, it can be treated as a quantitative variable and described in terms of centre and spread: ordinal variables often extend from the minimum to maximum possible values and in this case stating the range is not helpful. The meaning of the extremes should be stated in the context of the table to aid interpretation of results. Ordinal variables taking only a few distinct values are better treated as categorical variables and number (%) presented for each category. With only five categories the latter approach was adopted for ambulation score. Display as a categorical variable can be facilitated by combining infrequently occurring adjacent values.
In the original study, 3,182 of 5,719 admissions were screened and 2,286 were eligible. Six hundred and ten patients were not available on the hospital units when the RA [Research Assistant] arrived to complete the CAM [Confusion Assessment Method]; 1,582 patients assented to complete the CAM and 94 patients did not assent; the CAM was not completed for 728 patients because an informant was not available to confirm an acute change and fluctuation in mental status prior to admission or enrolment. The CAM was completed for 854 patients; 375 had delirium; 278 were enroled. Of the 278 enroled patients, 172 were discharged before the follow-up assessment, 73 were still hospitalised, 8 withdrew from the study and 27 died. Of the 172 discharged patients, delirium recovery status was determined for 152, 16 withdrew from the study after discharge and 4 died.
The authors start with the 5,719 admissions and report the numbers lost at successive stages, to arrive at the analysis sample of 152. It may be easier to assimilate the detail of the process from tabular or graphical presentation. The CONSORT guidelines [ 6 ] concerning the reporting of Randomised Controlled Trials (RCTs) recommend that progress of participants through a trial be presented as a flow chart, and an example is shown in Figure 2 . These charts are unequivocally helpful and are now presented in studies other than RCTs.
![research paper with descriptive statistics Recruitment and attrition rates in an RCT of WiiActive exercises in community dwelling older adults [7].](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/ageing/46/4/10.1093_ageing_afx054/5/m_afx054f02.jpeg?Expires=1727033620&Signature=aK4i~-fab4oGu4-JNk0zAb9UigzhvJzNKb96qaYpmIMq387xgnTQqBFkoMxSNJAkAEhA8uZh~90rWDfijnw-2wiEJBm7xbg4Lr0Cpa7kHicAe727GVdR~xbxFj3pvsSHxr40gDUBVUchhUKJgLse0k8J0MIkRmj8CpWAjRfFl3dn02XFB-7zSGVsS9Zm4pmmofX182Olz3jjVHFJXkCx5fGVaJWpcvkW80TXopDOCO6qSSI0eOI88nsO7mcnQBeyncNUOZZF91yHGIOPahni2Xmf0eIEMVxe94YMDZJw3GgfxbpxNHfUCigv3~0GApp4CCZTkhB1cHmWuF7nm8IixQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Recruitment and attrition rates in an RCT of WiiActive exercises in community dwelling older adults [ 7 ].
In addition to loss of participants at each time point as shown in a flow chart, information on specific variables may be missing even though a participant was available at the study point in question. Taking Table 1 as an example, there were 395 and 373 admissions during the 1998/99 and 2000/01 phases, respectively, as stated in the column headings, but the number of participants providing information varies considerably across the characteristics in the table. The reader should be able to establish how many cases contribute to each result, and to this end wherever the number available is lower than the total for the phase, it is stated below the descriptive statistics. For example, ambulation score was only available for 390 of the 395 participants in the 1998/99 phase. The percentages presented for ambulation score were calculated amongst cases where information was available, and this was done for all percentages in the table as indicated in the title. Alternatively, missing values in a categorical variable may be treated as a category in their own right. Where there is a large amount of missing information, this may be the best way of handling the situation with percentages calculated from the total sample size as denominator. Stating the numbers available allows the reader to check this point. Only participants whose operation was delayed by more than 48 h, gave a ‘reason why operation was delayed’ in the table, and from the stated numbers the reader can see that a reason was not given for all delayed cases.
In reports of RCTs, a table describing baseline characteristics in each trial arm demonstrates whether or not randomisation was successful in producing similar groups, as well as addressing the generalisability issue. If there are differences at baseline, comparison of outcome may be confounded. Statistical tests of significance should not be used to decide whether any differences need to be taken into account [ 8 , 9 ]. If the allocation was properly randomised, we know that any differences at baseline must be due to chance. The question facing the researcher is whether or not the magnitude of a difference at baseline is sufficient to confound comparison of outcome, and this depends on the strength of the relationship between the potential confounder and the outcome, as well the baseline difference. A statistical test for baseline differences does not address this question; furthermore, there may be insufficient numbers available to detect quite large baseline differences. Statistics describing baseline characteristics are used to judge whether any differences are large enough to be important. If they are, additional analyses of outcome controlled for characteristics that differ at baseline may be performed. On the other hand, in non-randomised studies, groups are likely to differ, and statistical significance tests can be used to evaluate the evidence that the selection process of patients to each intervention results in different groups. In this situation a primary analysis controlled for many predictors of outcome would probably have been planned, and should be carried out irrespective of any differences, or lack of them, between study groups.
Describing the main features of the distribution of important characteristics of the participants included in a study is the first step in most papers reporting statistical analysis. It is important in establishing the generalisability of research findings, and in the context of comparative studies, flags the need for controlled analysis. Usually space constraints limit the presentation of many descriptive statistics, and in any case, too many statistics can confuse rather than enhance insight. The attrition of subjects during a study should also be described, so that study subjects can be related to the patient base from which they were drawn.
Descriptive statistics are used to describe the participants in a study so that readers can assess the generalisability of study findings to their own clinical practice.
They need to be appropriate to the variable or participant characteristic they aim to describe, and presented in a fashion that is easy for readers to understand.
When many patient characteristics are being described, the detail of the statistics used and number of participants contributing to analysis are best incorporated in tabular presentation.
The author would like to thank Dr Helen Roberts for kindly granting permission to use data from the care pathway study [ 4 ] to produce Figure 1 c and d.
None declared.
Pickering RM . Describing the subjects in a study . Palliat Med 2001 ; 15 : 69 – 75 .
Google Scholar
Altman DG . Practical Statistics for Medical research . London : Chapman & Hall , 1991 .
Google Preview
Yeung P , Breheny M . Using the capability approach to understand the determinants of subjective well-being among community-dwelling older people in New Zealand . Age Aging 2016 ; 45 : 292 – 8 .
Roberts HC , Pickering RM , Onslow E et al. . The effectiveness of implementing a care pathway for femoral neck fracture in older people: a prospective controlled before and after study . Age Aging 2004 ; 33 : 178 – 84 .
Cole MG , McCusker JM , Bailey R et al. . Partial and no recovery from delirium after hospital discharge predict increased adverse events . Age Aging 2017 ; 46 : 90 – 5 .
Schulz KF , Altman DG , Moher D , for the CONSORT Group . CONSORT 2010 statement: updated guidelines for reporting parallel-group randomised trials . BMJ 2010 ; 340 : 698 – 702 .
Kwok BC , Pua YH . Effects of WiiActive exercises on fear of falling and functional outcomes in community-dwelling older adults: a randomised control trial . Age Aging 2016 ; 45 : 621 – 28 .
Assman SF , Pocock SJ , Enos LE , Kasten LE . Subgroup analysis and other (mis)uses of baseline data in clinical trials . Lancet 2000 ; 355 : 1064 – 9 .
Altman DG . Comparability of randomized groups . Statistician 1985 ; 34 : 125 – 36 .
- descriptive statistics
| Month: | Total Views: |
|---|---|
| May 2017 | 23 |
| June 2017 | 62 |
| July 2017 | 73 |
| August 2017 | 53 |
| September 2017 | 34 |
| October 2017 | 89 |
| November 2017 | 38 |
| December 2017 | 59 |
| January 2018 | 32 |
| February 2018 | 12 |
| March 2018 | 42 |
| April 2018 | 45 |
| May 2018 | 50 |
| June 2018 | 40 |
| July 2018 | 172 |
| August 2018 | 255 |
| September 2018 | 231 |
| October 2018 | 289 |
| November 2018 | 809 |
| December 2018 | 1,101 |
| January 2019 | 1,217 |
| February 2019 | 1,418 |
| March 2019 | 1,745 |
| April 2019 | 1,633 |
| May 2019 | 1,772 |
| June 2019 | 1,136 |
| July 2019 | 1,088 |
| August 2019 | 1,091 |
| September 2019 | 1,436 |
| October 2019 | 1,933 |
| November 2019 | 1,706 |
| December 2019 | 1,447 |
| January 2020 | 1,553 |
| February 2020 | 2,191 |
| March 2020 | 2,291 |
| April 2020 | 3,369 |
| May 2020 | 2,057 |
| June 2020 | 2,624 |
| July 2020 | 2,439 |
| August 2020 | 2,584 |
| September 2020 | 2,905 |
| October 2020 | 3,179 |
| November 2020 | 3,068 |
| December 2020 | 2,768 |
| January 2021 | 2,626 |
| February 2021 | 2,429 |
| March 2021 | 3,452 |
| April 2021 | 3,830 |
| May 2021 | 3,102 |
| June 2021 | 2,528 |
| July 2021 | 2,016 |
| August 2021 | 1,848 |
| September 2021 | 2,188 |
| October 2021 | 2,649 |
| November 2021 | 2,488 |
| December 2021 | 2,142 |
| January 2022 | 2,073 |
| February 2022 | 2,164 |
| March 2022 | 2,761 |
| April 2022 | 3,154 |
| May 2022 | 3,308 |
| June 2022 | 2,185 |
| July 2022 | 1,754 |
| August 2022 | 2,090 |
| September 2022 | 2,211 |
| October 2022 | 2,497 |
| November 2022 | 2,790 |
| December 2022 | 2,471 |
| January 2023 | 2,270 |
| February 2023 | 2,359 |
| March 2023 | 2,714 |
| April 2023 | 3,028 |
| May 2023 | 3,292 |
| June 2023 | 2,366 |
| July 2023 | 1,774 |
| August 2023 | 1,588 |
| September 2023 | 1,330 |
| October 2023 | 1,571 |
| November 2023 | 1,456 |
| December 2023 | 1,293 |
| January 2024 | 1,699 |
| February 2024 | 1,815 |
| March 2024 | 4,180 |
| April 2024 | 2,115 |
| May 2024 | 1,819 |
| June 2024 | 1,047 |
| July 2024 | 1,142 |
Email alerts
Citing articles via.
- Recommend to your Library
Affiliations
- Online ISSN 1468-2834
- Copyright © 2024 British Geriatrics Society
- About Oxford Academic
- Publish journals with us
- University press partners
- What we publish
- New features
- Open access
- Institutional account management
- Rights and permissions
- Get help with access
- Accessibility
- Media enquiries
- Oxford University Press
- Oxford Languages
- University of Oxford
Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide
- Copyright © 2024 Oxford University Press
- Cookie settings
- Cookie policy
- Privacy policy
- Legal notice
This Feature Is Available To Subscribers Only
Sign In or Create an Account
This PDF is available to Subscribers Only
For full access to this pdf, sign in to an existing account, or purchase an annual subscription.
Descriptive Statistics for Summarising Data
- First Online: 15 May 2020
Cite this chapter

- Ray W. Cooksey 2
38k Accesses
17 Citations
This chapter discusses and illustrates descriptive statistics . The purpose of the procedures and fundamental concepts reviewed in this chapter is quite straightforward: to facilitate the description and summarisation of data. By ‘describe’ we generally mean either the use of some pictorial or graphical representation of the data (e.g. a histogram, box plot, radar plot, stem-and-leaf display, icon plot or line graph) or the computation of an index or number designed to summarise a specific characteristic of a variable or measurement (e.g., frequency counts, measures of central tendency, variability, standard scores). Along the way, we explore the fundamental concepts of probability and the normal distribution. We seldom interpret individual data points or observations primarily because it is too difficult for the human brain to extract or identify the essential nature, patterns, or trends evident in the data, particularly if the sample is large. Rather we utilise procedures and measures which provide a general depiction of how the data are behaving. These statistical procedures are designed to identify or display specific patterns or trends in the data. What remains after their application is simply for us to interpret and tell the story.
You have full access to this open access chapter, Download chapter PDF
- Descriptive statistics
- Multivariate graphs
- Frequencies
- Central tendency
- Variability
- Standard scores
- Exploratory data analysis
- Probability
- Normal distribution
The first broad category of statistics we discuss concerns descriptive statistics . The purpose of the procedures and fundamental concepts in this category is quite straightforward: to facilitate the description and summarisation of data. By ‘describe’ we generally mean either the use of some pictorial or graphical representation of the data or the computation of an index or number designed to summarise a specific characteristic of a variable or measurement.
We seldom interpret individual data points or observations primarily because it is too difficult for the human brain to extract or identify the essential nature, patterns, or trends evident in the data, particularly if the sample is large. Rather we utilise procedures and measures which provide a general depiction of how the data are behaving. These statistical procedures are designed to identify or display specific patterns or trends in the data. What remains after their application is simply for us to interpret and tell the story.
Reflect on the QCI research scenario and the associated data set discussed in Chap. 4 . Consider the following questions that Maree might wish to address with respect to decision accuracy and speed scores:
What was the typical level of accuracy and decision speed for inspectors in the sample? [see Procedure 5.4 – Assessing central tendency.]
What was the most common accuracy and speed score amongst the inspectors? [see Procedure 5.4 – Assessing central tendency.]
What was the range of accuracy and speed scores; the lowest and the highest scores? [see Procedure 5.5 – Assessing variability.]
How frequently were different levels of inspection accuracy and speed observed? What was the shape of the distribution of inspection accuracy and speed scores? [see Procedure 5.1 – Frequency tabulation, distributions & crosstabulation.]
What percentage of inspectors would have ‘failed’ to ‘make the cut’ assuming the industry standard for acceptable inspection accuracy and speed combined was set at 95%? [see Procedure 5.7 – Standard ( z ) scores.]
How variable were the inspectors in their accuracy and speed scores? Were all the accuracy and speed levels relatively close to each other in magnitude or were the scores widely spread out over the range of possible test outcomes? [see Procedure 5.5 – Assessing variability.]
What patterns might be visually detected when looking at various QCI variables singly and together as a set? [see Procedure 5.2 – Graphical methods for dispaying data, Procedure 5.3 – Multivariate graphs & displays, and Procedure 5.6 – Exploratory data analysis.]
This chapter includes discussions and illustrations of a number of procedures available for answering questions about data like those posed above. In addition, you will find discussions of two fundamental concepts, namely probability and the normal distribution ; concepts that provide building blocks for Chaps. 6 and 7 .
Procedure 5.1: Frequency Tabulation, Distributions & Crosstabulation
Univariate (crosstabulations are bivariate); descriptive.
To produce an efficient counting summary of a sample of data points for ease of interpretation.
Any level of measurement can be used for a variable summarised in frequency tabulations and crosstabulations.
Frequency Tabulation and Distributions
Frequency tabulation serves to provide a convenient counting summary for a set of data that facilitates interpretation of various aspects of those data. Basically, frequency tabulation occurs in two stages:
First, the scores in a set of data are rank ordered from the lowest value to the highest value.
Second, the number of times each specific score occurs in the sample is counted. This count records the frequency of occurrence for that specific data value.
Consider the overall job satisfaction variable, jobsat , from the QCI data scenario. Performing frequency tabulation across the 112 Quality Control Inspectors on this variable using the SPSS Frequencies procedure (Allen et al. 2019 , ch. 3; George and Mallery 2019 , ch. 6) produces the frequency tabulation shown in Table 5.1 . Note that three of the inspectors in the sample did not provide a rating for jobsat thereby producing three missing values (= 2.7% of the sample of 112) and leaving 109 inspectors with valid data for the analysis.
The display of frequency tabulation is often referred to as the frequency distribution for the sample of scores. For each value of a variable, the frequency of its occurrence in the sample of data is reported. It is possible to compute various percentages and percentile values from a frequency distribution.
Table 5.1 shows the ‘Percent’ or relative frequency of each score (the percentage of the 112 inspectors obtaining each score, including those inspectors who were missing scores, which SPSS labels as ‘System’ missing). Table 5.1 also shows the ‘Valid Percent’ which is computed only for those inspectors in the sample who gave a valid or non-missing response.
Finally, it is possible to add up the ‘Valid Percent’ values, starting at the low score end of the distribution, to form the cumulative distribution or ‘Cumulative Percent’ . A cumulative distribution is useful for finding percentiles which reflect what percentage of the sample scored at a specific value or below.
We can see in Table 5.1 that 4 of the 109 valid inspectors (a ‘Valid Percent’ of 3.7%) indicated the lowest possible level of job satisfaction—a value of 1 (Very Low) – whereas 18 of the 109 valid inspectors (a ‘Valid Percent’ of 16.5%) indicated the highest possible level of job satisfaction—a value of 7 (Very High). The ‘Cumulative Percent’ number of 18.3 in the row for the job satisfaction score of 3 can be interpreted as “roughly 18% of the sample of inspectors reported a job satisfaction score of 3 or less”; that is, nearly a fifth of the sample expressed some degree of negative satisfaction with their job as a quality control inspector in their particular company.
If you have a large data set having many different scores for a particular variable, it may be more useful to tabulate frequencies on the basis of intervals of scores.
For the accuracy scores in the QCI database, you could count scores occurring in intervals such as ‘less than 75% accuracy’, ‘between 75% but less than 85% accuracy’, ‘between 85% but less than 95% accuracy’, and ‘95% accuracy or greater’, rather than counting the individual scores themselves. This would yield what is termed a ‘grouped’ frequency distribution since the data have been grouped into intervals or score classes. Producing such an analysis using SPSS would involve extra steps to create the new category or ‘grouping’ system for scores prior to conducting the frequency tabulation.
Crosstabulation
In a frequency crosstabulation , we count frequencies on the basis of two variables simultaneously rather than one; thus we have a bivariate situation.
For example, Maree might be interested in the number of male and female inspectors in the sample of 112 who obtained each jobsat score. Here there are two variables to consider: inspector’s gender and inspector’s j obsat score. Table 5.2 shows such a crosstabulation as compiled by the SPSS Crosstabs procedure (George and Mallery 2019 , ch. 8). Note that inspectors who did not report a score for jobsat and/or gender have been omitted as missing values, leaving 106 valid inspectors for the analysis.
The crosstabulation shown in Table 5.2 gives a composite picture of the distribution of satisfaction levels for male inspectors and for female inspectors. If frequencies or ‘Counts’ are added across the gender categories, we obtain the numbers in the ‘Total’ column (the percentages or relative frequencies are also shown immediately below each count) for each discrete value of jobsat (note this column of statistics differs from that in Table 5.1 because the gender variable was missing for certain inspectors). By adding down each gender column, we obtain, in the bottom row labelled ‘Total’, the number of males and the number of females that comprised the sample of 106 valid inspectors.
The totals, either across the rows or down the columns of the crosstabulation, are termed the marginal distributions of the table. These marginal distributions are equivalent to frequency tabulations for each of the variables jobsat and gender . As with frequency tabulation, various percentage measures can be computed in a crosstabulation, including the percentage of the sample associated with a specific count within either a row (‘% within jobsat ’) or a column (‘% within gender ’). You can see in Table 5.2 that 18 inspectors indicated a job satisfaction level of 7 (Very High); of these 18 inspectors reported in the ‘Total’ column, 8 (44.4%) were male and 10 (55.6%) were female. The marginal distribution for gender in the ‘Total’ row shows that 57 inspectors (53.8% of the 106 valid inspectors) were male and 49 inspectors (46.2%) were female. Of the 57 male inspectors in the sample, 8 (14.0%) indicated a job satisfaction level of 7 (Very High). Furthermore, we could generate some additional interpretive information of value by adding the ‘% within gender’ values for job satisfaction levels of 5, 6 and 7 (i.e. differing degrees of positive job satisfaction). Here we would find that 68.4% (= 24.6% + 29.8% + 14.0%) of male inspectors indicated some degree of positive job satisfaction compared to 61.2% (= 10.2% + 30.6% + 20.4%) of female inspectors.
This helps to build a picture of the possible relationship between an inspector’s gender and their level of job satisfaction (a relationship that, as we will see later, can be quantified and tested using Procedure 6.2 and Procedure 7.1 ).
It should be noted that a crosstabulation table such as that shown in Table 5.2 is often referred to as a contingency table about which more will be said later (see Procedure 7.1 and Procedure 7.18 ).
Frequency tabulation is useful for providing convenient data summaries which can aid in interpreting trends in a sample, particularly where the number of discrete values for a variable is relatively small. A cumulative percent distribution provides additional interpretive information about the relative positioning of specific scores within the overall distribution for the sample.
Crosstabulation permits the simultaneous examination of the distributions of values for two variables obtained from the same sample of observations. This examination can yield some useful information about the possible relationship between the two variables. More complex crosstabulations can be also done where the values of three or more variables are tracked in a single systematic summary. The use of frequency tabulation or cross-tabulation in conjunction with various other statistical measures, such as measures of central tendency (see Procedure 5.4 ) and measures of variability (see Procedure 5.5 ), can provide a relatively complete descriptive summary of any data set.
Disadvantages
Frequency tabulations can get messy if interval or ratio-level measures are tabulated simply because of the large number of possible data values. Grouped frequency distributions really should be used in such cases. However, certain choices, such as the size of the score interval (group size), must be made, often arbitrarily, and such choices can affect the nature of the final frequency distribution.
Additionally, percentage measures have certain problems associated with them, most notably, the potential for their misinterpretation in small samples. One should be sure to know the sample size on which percentage measures are based in order to obtain an interpretive reference point for the actual percentage values.
For example
In a sample of 10 individuals, 20% represents only two individuals whereas in a sample of 300 individuals, 20% represents 60 individuals. If all that is reported is the 20%, then the mental inference drawn by readers is likely to be that a sizeable number of individuals had a score or scores of a particular value—but what is ‘sizeable’ depends upon the total number of observations on which the percentage is based.
Where Is This Procedure Useful?
Frequency tabulation and crosstabulation are very commonly applied procedures used to summarise information from questionnaires, both in terms of tabulating various demographic characteristics (e.g. gender, age, education level, occupation) and in terms of actual responses to questions (e.g. numbers responding ‘yes’ or ‘no’ to a particular question). They can be particularly useful in helping to build up the data screening and demographic stories discussed in Chap. 4 . Categorical data from observational studies can also be analysed with this technique (e.g. the number of times Suzy talks to Frank, to Billy, and to John in a study of children’s social interactions).
Certain types of experimental research designs may also be amenable to analysis by crosstabulation with a view to drawing inferences about distribution differences across the sets of categories for the two variables being tracked.
You could employ crosstabulation in conjunction with the tests described in Procedure 7.1 to see if two different styles of advertising campaign differentially affect the product purchasing patterns of male and female consumers.
In the QCI database, Maree could employ crosstabulation to help her answer the question “do different types of electronic manufacturing firms ( company ) differ in terms of their tendency to employ male versus female quality control inspectors ( gender )?”
Software Procedures
Application | Procedures |
|---|---|
SPSS | or . and select the variable(s) you wish to analyse; for the procedure, hitting the ‘ ’ button will allow you to choose various types of statistics and percentages to show in each cell of the table. |
NCSS | or and select the variable(s) you wish to analyse. |
SYSTAT | or ➔ and select the variable(s) you wish to analyse and choose the optional statistics you wish to see. |
STATGRAPHICS | or and select the variable(s) you wish to analyse; hit ‘ ’ and when the ‘Tables and Graphs’ window opens, choose the Tables and Graphs you wish to see. |
Commander | or and select the variable(s) you wish to analyse and choose the optional statistics you wish to see. |
Procedure 5.2: Graphical Methods for Displaying Data
Univariate (scatterplots are bivariate); descriptive.
To visually summarise characteristics of a data sample for ease of interpretation.
Any level of measurement can be accommodated by these graphical methods. Scatterplots are generally used for interval or ratio-level data.
Graphical methods for displaying data include bar and pie charts, histograms and frequency polygons, line graphs and scatterplots. It is important to note that what is presented here is a small but representative sampling of the types of simple graphs one can produce to summarise and display trends in data. Generally speaking, SPSS offers the easiest facility for producing and editing graphs, but with a rather limited range of styles and types. SYSTAT, STATGRAPHICS and NCSS offer a much wider range of graphs (including graphs unique to each package), but with the drawback that it takes somewhat more effort to get the graphs in exactly the form you want.
Bar and Pie Charts
These two types of graphs are useful for summarising the frequency of occurrence of various values (or ranges of values) where the data are categorical (nominal or ordinal level of measurement).
A bar chart uses vertical and horizontal axes to summarise the data. The vertical axis is used to represent frequency (number) of occurrence or the relative frequency (percentage) of occurrence; the horizontal axis is used to indicate the data categories of interest.
A pie chart gives a simpler visual representation of category frequencies by cutting a circular plot into wedges or slices whose sizes are proportional to the relative frequency (percentage) of occurrence of specific data categories. Some pie charts can have a one or more slices emphasised by ‘exploding’ them out from the rest of the pie.
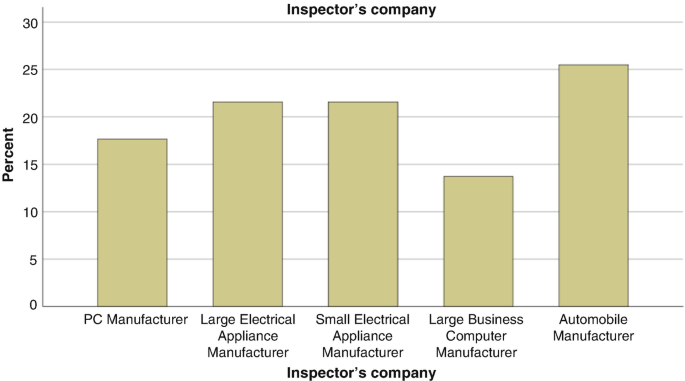
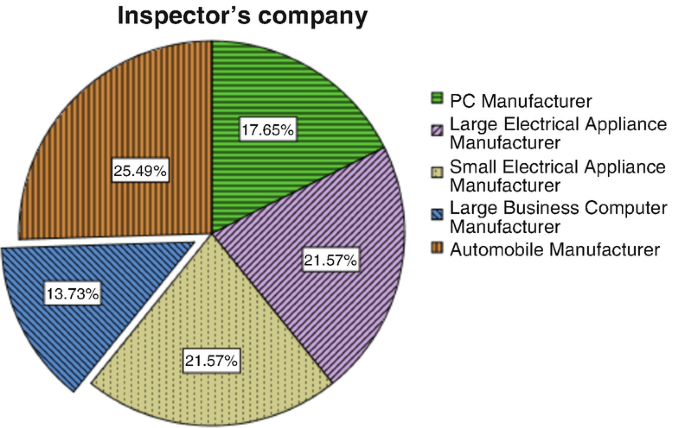
Consider the company variable from the QCI database. This variable depicts the types of manufacturing firms that the quality control inspectors worked for. Figure 5.1 illustrates a bar chart summarising the percentage of female inspectors in the sample coming from each type of firm. Figure 5.2 shows a pie chart representation of the same data, with an ‘exploded slice’ highlighting the percentage of female inspectors in the sample who worked for large business computer manufacturers – the lowest percentage of the five types of companies. Both graphs were produced using SPSS.
Bar chart: Percentage of female inspectors
Pie chart: Percentage of female inspectors
The pie chart was modified with an option to show the actual percentage along with the label for each category. The bar chart shows that computer manufacturing firms have relatively fewer female inspectors compared to the automotive and electrical appliance (large and small) firms. This trend is less clear from the pie chart which suggests that pie charts may be less visually interpretable when the data categories occur with rather similar frequencies. However, the ‘exploded slice’ option can help interpretation in some circumstances.
Certain software programs, such as SPSS, STATGRAPHICS, NCSS and Microsoft Excel, offer the option of generating 3-dimensional bar charts and pie charts and incorporating other ‘bells and whistles’ that can potentially add visual richness to the graphic representation of the data. However, you should generally be careful with these fancier options as they can produce distortions and create ambiguities in interpretation (e.g. see discussions in Jacoby 1997 ; Smithson 2000 ; Wilkinson 2009 ). Such distortions and ambiguities could ultimately end up providing misinformation to researchers as well as to those who read their research.
Histograms and Frequency Polygons
These two types of graphs are useful for summarising the frequency of occurrence of various values (or ranges of values) where the data are essentially continuous (interval or ratio level of measurement) in nature. Both histograms and frequency polygons use vertical and horizontal axes to summarise the data. The vertical axis is used to represent the frequency (number) of occurrence or the relative frequency (percentage) of occurrences; the horizontal axis is used for the data values or ranges of values of interest. The histogram uses bars of varying heights to depict frequency; the frequency polygon uses lines and points.
There is a visual difference between a histogram and a bar chart: the bar chart uses bars that do not physically touch, signifying the discrete and categorical nature of the data, whereas the bars in a histogram physically touch to signal the potentially continuous nature of the data.
Suppose Maree wanted to graphically summarise the distribution of speed scores for the 112 inspectors in the QCI database. Figure 5.3 (produced using NCSS) illustrates a histogram representation of this variable. Figure 5.3 also illustrates another representational device called the ‘density plot’ (the solid tracing line overlaying the histogram) which gives a smoothed impression of the overall shape of the distribution of speed scores. Figure 5.4 (produced using STATGRAPHICS) illustrates the frequency polygon representation for the same data.
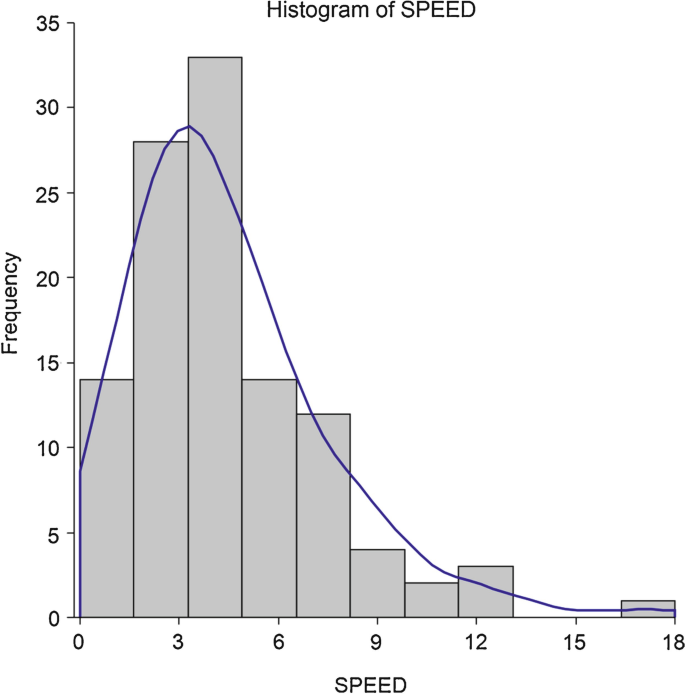
Histogram of the speed variable (with density plot overlaid)
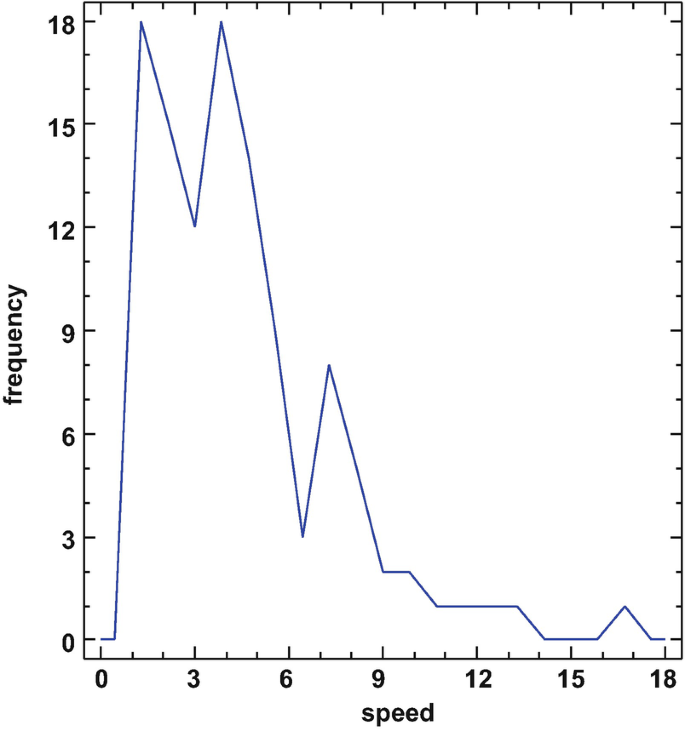
Frequency polygon plot of the speed variable
These graphs employ a grouped format where speed scores which fall within specific intervals are counted as being essentially the same score. The shape of the data distribution is reflected in these plots. Each graph tells us that the inspection speed scores are positively skewed with only a few inspectors taking very long times to make their inspection judgments and the majority of inspectors taking rather shorter amounts of time to make their decisions.
Both representations tell a similar story; the choice between them is largely a matter of personal preference. However, if the number of bars to be plotted in a histogram is potentially very large (and this is usually directly controllable in most statistical software packages), then a frequency polygon would be the preferred representation simply because the amount of visual clutter in the graph will be much reduced.
It is somewhat of an art to choose an appropriate definition for the width of the score grouping intervals (or ‘bins’ as they are often termed) to be used in the plot: choose too many and the plot may look too lumpy and the overall distributional trend may not be obvious; choose too few and the plot will be too coarse to give a useful depiction. Programs like SPSS, SYSTAT, STATGRAPHICS and NCSS are designed to choose an ‘appropriate’ number of bins to be used, but the analyst’s eye is often a better judge than any statistical rule that a software package would use.
There are several interesting variations of the histogram which can highlight key data features or facilitate interpretation of certain trends in the data. One such variation is a graph is called a dual histogram (available in SYSTAT; a variation called a ‘comparative histogram’ can be created in NCSS) – a graph that facilitates visual comparison of the frequency distributions for a specific variable for participants from two distinct groups.
Suppose Maree wanted to graphically compare the distributions of speed scores for inspectors in the two categories of education level ( educlev ) in the QCI database. Figure 5.5 shows a dual histogram (produced using SYSTAT) that accomplishes this goal. This graph still employs the grouped format where speed scores falling within particular intervals are counted as being essentially the same score. The shape of the data distribution within each group is also clearly reflected in this plot. However, the story conveyed by the dual histogram is that, while the inspection speed scores are positively skewed for inspectors in both categories of educlev, the comparison suggests that inspectors with a high school level of education (= 1) tend to take slightly longer to make their inspection decisions than do their colleagues who have a tertiary qualification (= 2).
Dual histogram of speed for the two categories of educlev
Line Graphs
The line graph is similar in style to the frequency polygon but is much more general in its potential for summarising data. In a line graph, we seldom deal with percentage or frequency data. Instead we can summarise other types of information about data such as averages or means (see Procedure 5.4 for a discussion of this measure), often for different groups of participants. Thus, one important use of the line graph is to break down scores on a specific variable according to membership in the categories of a second variable.
In the context of the QCI database, Maree might wish to summarise the average inspection accuracy scores for the inspectors from different types of manufacturing companies. Figure 5.6 was produced using SPSS and shows such a line graph.
Line graph comparison of companies in terms of average inspection accuracy
Note how the trend in performance across the different companies becomes clearer with such a visual representation. It appears that the inspectors from the Large Business Computer and PC manufacturing companies have better average inspection accuracy compared to the inspectors from the remaining three industries.
With many software packages, it is possible to further elaborate a line graph by including error or confidence intervals bars (see Procedure 8.3 ). These give some indication of the precision with which the average level for each category in the population has been estimated (narrow bars signal a more precise estimate; wide bars signal a less precise estimate).
Figure 5.7 shows such an elaborated line graph, using 95% confidence interval bars, which can be used to help make more defensible judgments (compared to Fig. 5.6 ) about whether the companies are substantively different from each other in average inspection performance. Companies whose confidence interval bars do not overlap each other can be inferred to be substantively different in performance characteristics.
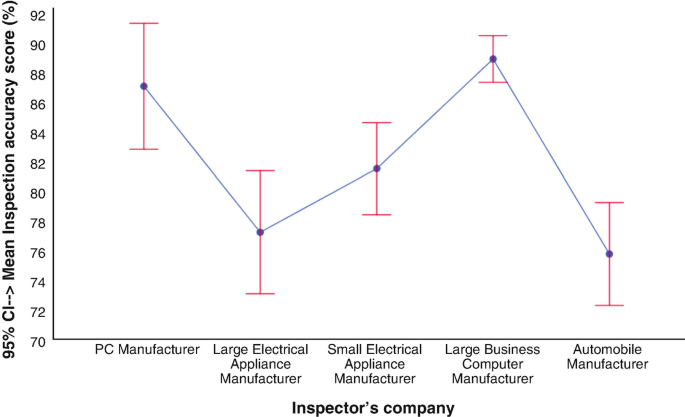
Line graph using confidence interval bars to compare accuracy across companies
The accuracy confidence interval bars for participants from the Large Business Computer manufacturing firms do not overlap those from the Large or Small Electrical Appliance manufacturers or the Automobile manufacturers.
We might conclude that quality control inspection accuracy is substantially better in the Large Business Computer manufacturing companies than in these other industries but is not substantially better than the PC manufacturing companies. We might also conclude that inspection accuracy in PC manufacturing companies is not substantially different from Small Electrical Appliance manufacturers.
Scatterplots
Scatterplots are useful in displaying the relationship between two interval- or ratio-scaled variables or measures of interest obtained on the same individuals, particularly in correlational research (see Fundamental Concept III and Procedure 6.1 ).
In a scatterplot, one variable is chosen to be represented on the horizontal axis; the second variable is represented on the vertical axis. In this type of plot, all data point pairs in the sample are graphed. The shape and tilt of the cloud of points in a scatterplot provide visual information about the strength and direction of the relationship between the two variables. A very compact elliptical cloud of points signals a strong relationship; a very loose or nearly circular cloud signals a weak or non-existent relationship. A cloud of points generally tilted upward toward the right side of the graph signals a positive relationship (higher scores on one variable associated with higher scores on the other and vice-versa). A cloud of points generally tilted downward toward the right side of the graph signals a negative relationship (higher scores on one variable associated with lower scores on the other and vice-versa).
Maree might be interested in displaying the relationship between inspection accuracy and inspection speed in the QCI database. Figure 5.8 , produced using SPSS, shows what such a scatterplot might look like. Several characteristics of the data for these two variables can be noted in Fig. 5.8 . The shape of the distribution of data points is evident. The plot has a fan-shaped characteristic to it which indicates that accuracy scores are highly variable (exhibit a very wide range of possible scores) at very fast inspection speeds but get much less variable and tend to be somewhat higher as inspection speed increases (where inspectors take longer to make their quality control decisions). Thus, there does appear to be some relationship between inspection accuracy and inspection speed (a weak positive relationship since the cloud of points tends to be very loose but tilted generally upward toward the right side of the graph – slower speeds tend to be slightly associated with higher accuracy.
Scatterplot relating inspection accuracy to inspection speed
However, it is not the case that the inspection decisions which take longest to make are necessarily the most accurate (see the labelled points for inspectors 7 and 62 in Fig. 5.8 ). Thus, Fig. 5.8 does not show a simple relationship that can be unambiguously summarised by a statement like “the longer an inspector takes to make a quality control decision, the more accurate that decision is likely to be”. The story is more complicated.
Some software packages, such as SPSS, STATGRAPHICS and SYSTAT, offer the option of using different plotting symbols or markers to represent the members of different groups so that the relationship between the two focal variables (the ones anchoring the X and Y axes) can be clarified with reference to a third categorical measure.
Maree might want to see if the relationship depicted in Fig. 5.8 changes depending upon whether the inspector was tertiary-qualified or not (this information is represented in the educlev variable of the QCI database).
Figure 5.9 shows what such a modified scatterplot might look like; the legend in the upper corner of the figure defines the marker symbols for each category of the educlev variable. Note that for both High School only-educated inspectors and Tertiary-qualified inspectors, the general fan-shaped relationship between accuracy and speed is the same. However, it appears that the distribution of points for the High School only-educated inspectors is shifted somewhat upward and toward the right of the plot suggesting that these inspectors tend to be somewhat more accurate as well as slower in their decision processes.
Scatterplot displaying accuracy vs speed conditional on educlev group
There are many other styles of graphs available, often dependent upon the specific statistical package you are using. Interestingly, NCSS and, particularly, SYSTAT and STATGRAPHICS, appear to offer the most variety in terms of types of graphs available for visually representing data. A reading of the user’s manuals for these programs (see the Useful additional readings) would expose you to the great diversity of plotting techniques available to researchers. Many of these techniques go by rather interesting names such as: Chernoff’s faces, radar plots, sunflower plots, violin plots, star plots, Fourier blobs, and dot plots.
These graphical methods provide summary techniques for visually presenting certain characteristics of a set of data. Visual representations are generally easier to understand than a tabular representation and when these plots are combined with available numerical statistics, they can give a very complete picture of a sample of data. Newer methods have become available which permit more complex representations to be depicted, opening possibilities for creatively visually representing more aspects and features of the data (leading to a style of visual data storytelling called infographics ; see, for example, McCandless 2014 ; Toseland and Toseland 2012 ). Many of these newer methods can display data patterns from multiple variables in the same graph (several of these newer graphical methods are illustrated and discussed in Procedure 5.3 ).
Graphs tend to be cumbersome and space consuming if a great many variables need to be summarised. In such cases, using numerical summary statistics (such as means or correlations) in tabular form alone will provide a more economical and efficient summary. Also, it can be very easy to give a misleading picture of data trends using graphical methods by simply choosing the ‘correct’ scaling for maximum effect or choosing a display option (such as a 3-D effect) that ‘looks’ presentable but which actually obscures a clear interpretation (see Smithson 2000 ; Wilkinson 2009 ).
Thus, you must be careful in creating and interpreting visual representations so that the influence of aesthetic choices for sake of appearance do not become more important than obtaining a faithful and valid representation of the data—a very real danger with many of today’s statistical packages where ‘default’ drawing options have been pre-programmed in. No single plot can completely summarise all possible characteristics of a sample of data. Thus, choosing a specific method of graphical display may, of necessity, force a behavioural researcher to represent certain data characteristics (such as frequency) at the expense of others (such as averages).
Virtually any research design which produces quantitative data and statistics (even to the extent of just counting the number of occurrences of several events) provides opportunities for graphical data display which may help to clarify or illustrate important data characteristics or relationships. Remember, graphical displays are communication tools just like numbers—which tool to choose depends upon the message to be conveyed. Visual representations of data are generally more useful in communicating to lay persons who are unfamiliar with statistics. Care must be taken though as these same lay people are precisely the people most likely to misinterpret a graph if it has been incorrectly drawn or scaled.
Application | Procedures |
|---|---|
SPSS | and choose from a range of gallery chart types: , ; drag the chart type into the working area and customise the chart with desired variables, labels, etc. many elements of a chart, including error bars, can be controlled. |
NCSS | or or or or or hichever type of chart you choose, you can control many features of the chart from the dialog box that pops open upon selection. |
STATGRAPHICS | or or or hichever type of chart you choose, you can control a number of features of the chart from the series of dialog boxes that pops open upon selection. |
SYSTAT | or or or or or (which offers a range of other more novel graphical displays, including the dual histogram). For each choice, a dialog box opens which allows you to control almost every characteristic of the graph you want. |
Commander | or or or or ; for some graphs ( being the exception), there is minimal control offered by Commander over the appearance of the graph (you need to use full commands to control more aspects; e.g. see Chang ). |
Procedure 5.3: Multivariate Graphs & Displays
Multivariate; descriptive.
To simultaneously and visually summarise characteristics of many variables obtained on the same entities for ease of interpretation.
Multivariate graphs and displays are generally produced using interval or ratio-level data. However, such graphs may be grouped according to a nominal or ordinal categorical variable for comparison purposes.
Graphical methods for displaying multivariate data (i.e. many variables at once) include scatterplot matrices, radar (or spider) plots, multiplots, parallel coordinate displays, and icon plots. Multivariate graphs are useful for visualising broad trends and patterns across many variables (Cleveland 1995 ; Jacoby 1998 ). Such graphs typically sacrifice precision in representation in favour of a snapshot pictorial summary that can help you form general impressions of data patterns.
It is important to note that what is presented here is a small but reasonably representative sampling of the types of graphs one can produce to summarise and display trends in multivariate data. Generally speaking, SYSTAT offers the best facilities for producing multivariate graphs, followed by STATGRAPHICS, but with the drawback that it is somewhat tricky to get the graphs in exactly the form you want. SYSTAT also has excellent facilities for creating new forms and combinations of graphs – essentially allowing graphs to be tailor-made for a specific communication purpose. Both SPSS and NCSS offer a more limited range of multivariate graphs, generally restricted to scatterplot matrices and variations of multiplots. Microsoft Excel or STATGRAPHICS are the packages to use if radar or spider plots are desired.
Scatterplot Matrices
A scatterplot matrix is a useful multivariate graph designed to show relationships between pairs of many variables in the same display.
Figure 5.10 illustrates a scatterplot matrix, produced using SYSTAT, for the mentabil , accuracy , speed , jobsat and workcond variables in the QCI database. It is easy to see that all the scatterplot matrix does is stack all pairs of scatterplots into a format where it is easy to pick out the graph for any ‘row’ variable that intersects a column ‘variable’.
Scatterplot matrix relating mentabil , accuracy , speed , jobsat & workcond
In those plots where a ‘row’ variable intersects itself in a column of the matrix (along the so-called ‘diagonal’), SYSTAT permits a range of univariate displays to be shown. Figure 5.10 shows univariate histograms for each variable (recall Procedure 5.2 ). One obvious drawback of the scatterplot matrix is that, if many variables are to be displayed (say ten or more); the graph gets very crowded and becomes very hard to visually appreciate.
Looking at the first column of graphs in Fig. 5.10 , we can see the scatterplot relationships between mentabil and each of the other variables. We can get a visual impression that mentabil seems to be slightly negatively related to accuracy (the cloud of scatter points tends to angle downward to the right, suggesting, very slightly, that higher mentabil scores are associated with lower levels of accuracy ).
Conversely, the visual impression of the relationship between mentabil and speed is that the relationship is slightly positive (higher mentabil scores tend to be associated with higher speed scores = longer inspection times). Similar types of visual impressions can be formed for other parts of Fig. 5.10 . Notice that the histogram plots along the diagonal give a clear impression of the shape of the distribution for each variable.
Radar Plots
The radar plot (also known as a spider graph for obvious reasons) is a simple and effective device for displaying scores on many variables. Microsoft Excel offers a range of options and capabilities for producing radar plots, such as the plot shown in Fig. 5.11 . Radar plots are generally easy to interpret and provide a good visual basis for comparing plots from different individuals or groups, even if a fairly large number of variables (say, up to about 25) are being displayed. Like a clock face, variables are evenly spaced around the centre of the plot in clockwise order starting at the 12 o’clock position. Visual interpretation of a radar plot primarily relies on shape comparisons, i.e. the rise and fall of peaks and valleys along the spokes around the plot. Valleys near the centre display low scores on specific variables, peaks near the outside of the plot display high scores on specific variables. [Note that, technically, radar plots employ polar coordinates.] SYSTAT can draw graphs using polar coordinates but not as easily as Excel can, from the user’s perspective. Radar plots work best if all the variables represented are measured on the same scale (e.g. a 1 to 7 Likert-type scale or 0% to 100% scale). Individuals who are missing any scores on the variables being plotted are typically omitted.
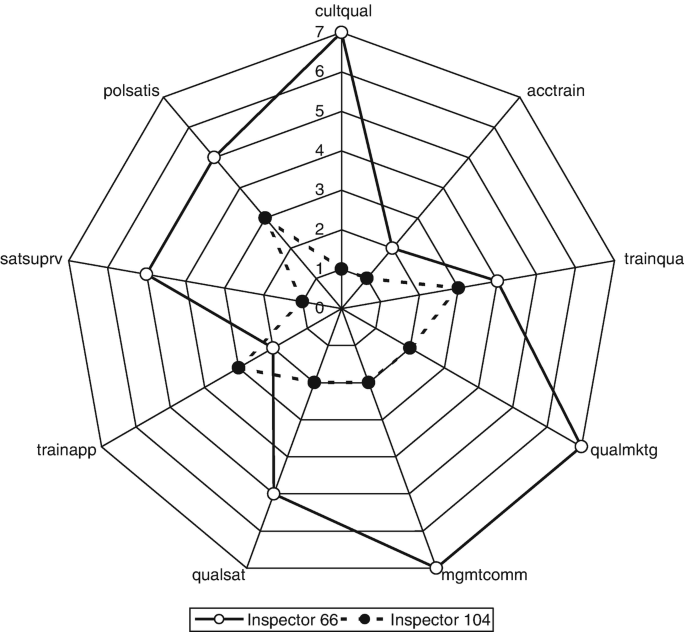
Radar plot comparing attitude ratings for inspectors 66 and 104
The radar plot in Fig. 5.11 , produced using Excel, compares two specific inspectors, 66 and 104, on the nine attitude rating scales. Inspector 66 gave the highest rating (= 7) on the cultqual variable and inspector 104 gave the lowest rating (= 1). The plot shows that inspector 104 tended to provide very low ratings on all nine attitude variables, whereas inspector 66 tended to give very high ratings on all variables except acctrain and trainapp , where the scores were similar to those for inspector 104. Thus, in general, inspector 66 tended to show much more positive attitudes toward their workplace compared to inspector 104.
While Fig. 5.11 was generated to compare the scores for two individuals in the QCI database, it would be just as easy to produce a radar plot that compared the five types of companies in terms of their average ratings on the nine variables, as shown in Fig. 5.12 .
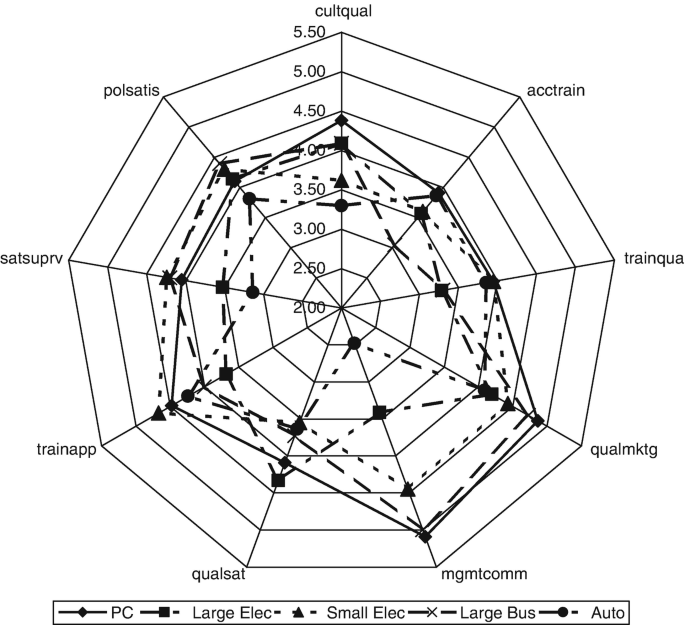
Radar plot comparing average attitude ratings for five types of company
Here we can form the visual impression that the five types of companies differ most in their average ratings of mgmtcomm and least in the average ratings of polsatis . Overall, the average ratings from inspectors from PC manufacturers (black diamonds with solid lines) seem to be generally the most positive as their scores lie on or near the outer ring of scores and those from Automobile manufacturers tend to be least positive on many variables (except the training-related variables).
Extrapolating from Fig. 5.12 , you may rightly conclude that including too many groups and/or too many variables in a radar plot comparison can lead to so much clutter that any visual comparison would be severely degraded. You may have to experiment with using colour-coded lines to represent different groups versus line and marker shape variations (as used in Fig. 5.12 ), because choice of coding method for groups can influence the interpretability of a radar plot.
A multiplot is simply a hybrid style of graph that can display group comparisons across a number of variables. There are a wide variety of possible multiplots one could potentially design (SYSTAT offers great capabilities with respect to multiplots). Figure 5.13 shows a multiplot comprising a side-by-side series of profile-based line graphs – one graph for each type of company in the QCI database.
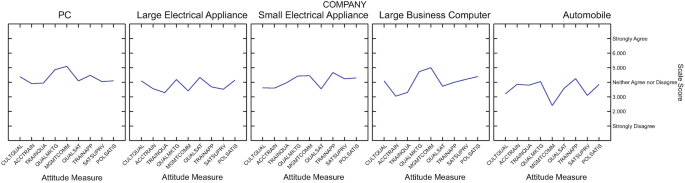
Multiplot comparing profiles of average attitude ratings for five company types
The multiplot in Fig. 5.13 , produced using SYSTAT, graphs the profile of average attitude ratings for all inspectors within a specific type of company. This multiplot shows the same story as the radar plot in Fig. 5.12 , but in a different graphical format. It is still fairly clear that the average ratings from inspectors from PC manufacturers tend to be higher than for the other types of companies and the profile for inspectors from automobile manufacturers tends to be lower than for the other types of companies.
The profile for inspectors from large electrical appliance manufacturers is the flattest, meaning that their average attitude ratings were less variable than for other types of companies. Comparing the ease with which you can glean the visual impressions from Figs. 5.12 and 5.13 may lead you to prefer one style of graph over another. If you have such preferences, chances are others will also, which may mean you need to carefully consider your options when deciding how best to display data for effect.
Frequently, choice of graph is less a matter of which style is right or wrong, but more a matter of which style will suit specific purposes or convey a specific story, i.e. the choice is often strategic.
Parallel Coordinate Displays
A parallel coordinate display is useful for displaying individual scores on a range of variables, all measured using the same scale. Furthermore, such graphs can be combined side-by-side to facilitate very broad visual comparisons among groups, while retaining individual profile variability in scores. Each line in a parallel coordinate display represents one individual, e.g. an inspector.
The interpretation of a parallel coordinate display, such as the two shown in Fig. 5.14 , depends on visual impressions of the peaks and valleys (highs and lows) in the profiles as well as on the density of similar profile lines. The graph is called ‘parallel coordinate’ simply because it assumes that all variables are measured on the same scale and that scores for each variable can therefore be located along vertical axes that are parallel to each other (imagine vertical lines on Fig. 5.14 running from bottom to top for each variable on the X-axis). The main drawback of this method of data display is that only those individuals in the sample who provided legitimate scores on all of the variables being plotted (i.e. who have no missing scores) can be displayed.
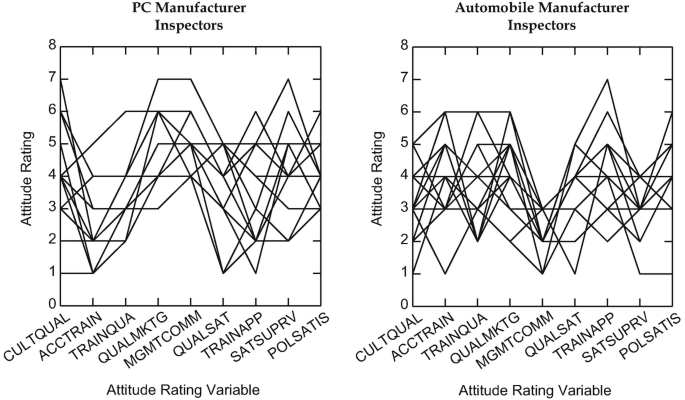
Parallel coordinate displays comparing profiles of average attitude ratings for five company types
The parallel coordinate display in Fig. 5.14 , produced using SYSTAT, graphs the profile of average attitude ratings for all inspectors within two specific types of company: the left graph for inspectors from PC manufacturers and the right graph for automobile manufacturers.
There are fewer lines in each display than the number of inspectors from each type of company simply because several inspectors from each type of company were missing a rating on at least one of the nine attitude variables. The graphs show great variability in scores amongst inspectors within a company type, but there are some overall patterns evident.
For example, inspectors from automobile companies clearly and fairly uniformly rated mgmtcomm toward the low end of the scale, whereas the reverse was generally true for that variable for inspectors from PC manufacturers. Conversely, inspectors from automobile companies tend to rate acctrain and trainapp more toward the middle to high end of the scale, whereas the reverse is generally true for those variables for inspectors from PC manufacturers.
Perhaps the most creative types of multivariate displays are the so-called icon plots . SYSTAT and STATGRAPHICS offer an impressive array of different types of icon plots, including, amongst others, Chernoff’s faces, profile plots, histogram plots, star glyphs and sunray plots (Jacoby 1998 provides a detailed discussion of icon plots).
Icon plots generally use a specific visual construction to represent variables scores obtained by each individual within a sample or group. All icon plots are thus methods for displaying the response patterns for individual members of a sample, as long as those individuals are not missing any scores on the variables to be displayed (note that this is the same limitation as for radar plots and parallel coordinate displays). To illustrate icon plots, without generating too many icons to focus on, Figs. 5.15 , 5.16 , 5.17 and 5.18 present four different icon plots for QCI inspectors classified, using a new variable called BEST_WORST , as either the worst performers (= 1 where their accuracy scores were less than 70%) or the best performers (= 2 where their accuracy scores were 90% or greater).
Chernoff’s faces icon plot comparing individual attitude ratings for best and worst performing inspectors
Profile plot comparing individual attitude ratings for best and worst performing inspectors
Histogram plot comparing individual attitude ratings for best and worst performing inspectors
Sunray plot comparing individual attitude ratings for best and worst performing inspectors
The Chernoff’s faces plot gets its name from the visual icon used to represent variable scores – a cartoon-type face. This icon tries to capitalise on our natural human ability to recognise and differentiate faces. Each feature of the face is controlled by the scores on a single variable. In SYSTAT, up to 20 facial features are controllable; the first five being curvature of mouth, angle of brow, width of nose, length of nose and length of mouth (SYSTAT Software Inc., 2009 , p. 259). The theory behind Chernoff’s faces is that similar patterns of variable scores will produce similar looking faces, thereby making similarities and differences between individuals more apparent.
The profile plot and histogram plot are actually two variants of the same type of icon plot. A profile plot represents individuals’ scores for a set of variables using simplified line graphs, one per individual. The profile is scaled so that the vertical height of the peaks and valleys correspond to actual values for variables where the variables anchor the X-axis in a fashion similar to the parallel coordinate display. So, as you examine a profile from left to right across the X-axis of each graph, you are looking across the set of variables. A histogram plot represents the same information in the same way as for the profile plot but using histogram bars instead.
Figure 5.15 , produced using SYSTAT, shows a Chernoff’s faces plot for the best and worst performing inspectors using their ratings of job satisfaction, working conditions and the nine general attitude statements.
Each face is labelled with the inspector number it represents. The gaps indicate where an inspector had missing data on at least one of the variables, meaning a face could not be generated for them. The worst performers are drawn using red lines; the best using blue lines. The first variable is jobsat and this variable controls mouth curvature; the second variable is workcond and this controls angle of brow, and so on. It seems clear that there are differences in the faces between the best and worst performers with, for example, best performers tending to be more satisfied (smiling) and with higher ratings for working conditions (brow angle).
Beyond a broad visual impression, there is little in terms of precise inferences you can draw from a Chernoff’s faces plot. It really provides a visual sketch, nothing more. The fact that there is no obvious link between facial features, variables and score levels means that the Chernoff’s faces icon plot is difficult to interpret at the level of individual variables – a holistic impression of similarity and difference is what this type of plot facilitates.
Figure 5.16 produced using SYSTAT, shows a profile plot for the best and worst performing inspectors using their ratings of job satisfaction, working conditions and the nine attitude variables.
Like the Chernoff’s faces plot (Fig. 5.15 ), as you read across the rows of the plot from left to right, each plot corresponds respectively to a inspector in the sample who was either in the worst performer (red) or best performer (blue) category. The first attitude variable is jobsat and anchors the left end of each line graph; the last variable is polsatis and anchors the right end of the line graph. The remaining variables are represented in order from left to right across the X-axis of each graph. Figure 5.16 shows that these inspectors are rather different in their attitude profiles, with best performers tending to show taller profiles on the first two variables, for example.
Figure 5.17 produced using SYSTAT, shows a histogram plot for the best and worst performing inspectors based on their ratings of job satisfaction, working conditions and the nine attitude variables. This plot tells the same story as the profile plot, only using histogram bars. Some people would prefer the histogram icon plot to the profile plot because each histogram bar corresponds to one variable, making the visual linking of a specific bar to a specific variable much easier than visually linking a specific position along the profile line to a specific variable.
The sunray plot is actually a simplified adaptation of the radar plot (called a “star glyph”) used to represent scores on a set of variables for each individual within a sample or group. Remember that a radar plot basically arranges the variables around a central point like a clock face; the first variable is represented at the 12 o’clock position and the remaining variables follow around the plot in a clockwise direction.
Unlike a radar plot, while the spokes (the actual ‘star’ of the glyph’s name) of the plot are visible, no interpretive scale is evident. A variable’s score is visually represented by its distance from the central point. Thus, the star glyphs in a sunray plot are designed, like Chernoff’s faces, to provide a general visual impression, based on icon shape. A wide diameter well-rounded plot indicates an individual with high scores on all variables and a small diameter well-rounded plot vice-versa. Jagged plots represent individuals with highly variable scores across the variables. ‘Stars’ of similar size, shape and orientation represent similar individuals.
Figure 5.18 , produced using STATGRAPHICS, shows a sunray plot for the best and worst performing inspectors. An interpretation glyph is also shown in the lower right corner of Fig. 5.18 , where variables are aligned with the spokes of a star (e.g. jobsat is at the 12 o’clock position). This sunray plot could lead you to form the visual impression that the worst performing inspectors (group 1) have rather less rounded rating profiles than do the best performing inspectors (group 2) and that the jobsat and workcond spokes are generally lower for the worst performing inspectors.
Comparatively speaking, the sunray plot makes identifying similar individuals a bit easier (perhaps even easier than Chernoff’s faces) and, when ordered as STATGRAPHICS showed in Fig. 5.18 , permits easier visual comparisons between groups of individuals, but at the expense of precise knowledge about variable scores. Remember, a holistic impression is the goal pursued using a sunray plot.
Multivariate graphical methods provide summary techniques for visually presenting certain characteristics of a complex array of data on variables. Such visual representations are generally better at helping us to form holistic impressions of multivariate data rather than any sort of tabular representation or numerical index. They also allow us to compress many numerical measures into a finite representation that is generally easy to understand. Multivariate graphical displays can add interest to an otherwise dry statistical reporting of numerical data. They are designed to appeal to our pattern recognition skills, focusing our attention on features of the data such as shape, level, variability and orientation. Some multivariate graphs (e.g. radar plots, sunray plots and multiplots) are useful not only for representing score patterns for individuals but also providing summaries of score patterns across groups of individuals.
Multivariate graphs tend to get very busy-looking and are hard to interpret if a great many variables or a large number of individuals need to be displayed (imagine any of the icon plots, for a sample of 200 questionnaire participants, displayed on a A4 page – each icon would be so small that its features could not be easily distinguished, thereby defeating the purpose of the display). In such cases, using numerical summary statistics (such as averages or correlations) in tabular form alone will provide a more economical and efficient summary. Also, some multivariate displays will work better for conveying certain types of information than others.
Information about variable relationships may be better displayed using a scatterplot matrix. Information about individual similarities and difference on a set of variables may be better conveyed using a histogram or sunray plot. Multiplots may be better suited to displaying information about group differences across a set of variables. Information about the overall similarity of individual entities in a sample might best be displayed using Chernoff’s faces.
Because people differ greatly in their visual capacities and preferences, certain types of multivariate displays will work for some people and not others. Sometimes, people will not see what you see in the plots. Some plots, such as Chernoff’s faces, may not strike a reader as a serious statistical procedure and this could adversely influence how convinced they will be by the story the plot conveys. None of the multivariate displays described here provide sufficiently precise information for solid inferences or interpretations; all are designed to simply facilitate the formation of holistic visual impressions. In fact, you may have noticed that some displays (scatterplot matrices and the icon plots, for example) provide no numerical scaling information that would help make precise interpretations. If precision in summary information is desired, the types of multivariate displays discussed here would not be the best strategic choices.
Virtually any research design which produces quantitative data/statistics for multiple variables provides opportunities for multivariate graphical data display which may help to clarify or illustrate important data characteristics or relationships. Thus, for survey research involving many identically-scaled attitudinal questions, a multivariate display may be just the device needed to communicate something about patterns in the data. Multivariate graphical displays are simply specialised communication tools designed to compress a lot of information into a meaningful and efficient format for interpretation—which tool to choose depends upon the message to be conveyed.
Generally speaking, visual representations of multivariate data could prove more useful in communicating to lay persons who are unfamiliar with statistics or who prefer visual as opposed to numerical information. However, these displays would probably require some interpretive discussion so that the reader clearly understands their intent.
Application | Procedures |
|---|---|
SPSS | and choose from the gallery; drag the chart type into the working area and customise the chart with desired variables, labels, etc. Only a few elements of each chart can be configured and altered. |
NCSS | Only a few elements of this plot are customisable in NCSS. |
SYSTAT | (and you can select what type of plot you want to appear in the diagonal boxes) or ( can be selected by choosing a variable. e.g. ) or or (for icon plots, you can choose from a range of icons including Chernoff’s faces, histogram, star, sun or profile amongst others). A large number of elements of each type of plot are easily customisable, although it may take some trial and error to get exactly the look you want. |
STATGRAPHICS | or or or Several elements of each type of plot are easily customisable, although it may take some trial and error to get exactly the look you want. |
commander | You can select what type of plot you want to appear in the diagonal boxes, and you can control some other features of the plot. Other multivariate data displays are available via various packages (e.g. the or package), but not through commander. |
Procedure 5.4: Assessing Central Tendency
Univariate; descriptive.
To provide numerical summary measures that give an indication of the central, average or typical score in a distribution of scores for a variable.
Mean – variables should be measured at the interval or ratio-level.
Median – variables should be measured at least at the ordinal-level.
Mode – variables can be measured at any of the four levels.
The three most commonly reported measures of central tendency are the mean, median and mode. Each measure reflects a specific way of defining central tendency in a distribution of scores on a variable and each has its own advantages and disadvantages.
The mean is the most widely used measure of central tendency (also called the arithmetic average). Very simply, a mean is the sum of all the scores for a specific variable in a sample divided by the number of scores used in obtaining the sum. The resulting number reflects the average score for the sample of individuals on which the scores were obtained. If one were asked to predict the score that any single individual in the sample would obtain, the best prediction, in the absence of any other relevant information, would be the sample mean. Many parametric statistical methods (such as Procedures 7.2 , 7.4 , 7.6 and 7.10 ) deal with sample means in one way or another. For any sample of data, there is one and only one possible value for the mean in a specific distribution. For most purposes, the mean is the preferred measure of central tendency because it utilises all the available information in a sample.
In the context of the QCI database, Maree could quite reasonably ask what inspectors scored on the average in terms of mental ability ( mentabil ), inspection accuracy ( accuracy ), inspection speed ( speed ), overall job satisfaction ( jobsat ), and perceived quality of their working conditions ( workcond ). Table 5.3 shows the mean scores for the sample of 112 quality control inspectors on each of these variables. The statistics shown in Table 5.3 were computed using the SPSS Frequencies ... procedure. Notice that the table indicates how many of the 112 inspectors had a valid score for each variable and how many were missing a score (e.g. 109 inspectors provided a valid rating for jobsat; 3 inspectors did not).
Each mean needs to be interpreted in terms of the original units of measurement for each variable. Thus, the inspectors in the sample showed an average mental ability score of 109.84 (higher than the general population mean of 100 for the test), an average inspection accuracy of 82.14%, and an average speed for making quality control decisions of 4.48 s. Furthermore, in terms of their work context, inspectors reported an average overall job satisfaction of 4.96 (on the 7-point scale, or a level of satisfaction nearly one full scale point above the Neutral point of 4—indicating a generally positive but not strong level of job satisfaction, and an average perceived quality of work conditions of 4.21 (on the 7-point scale which is just about at the level of Stressful but Tolerable.
The mean is sensitive to the presence of extreme values, which can distort its value, giving a biased indication of central tendency. As we will see below, the median is an alternative statistic to use in such circumstances. However, it is also possible to compute what is called a trimmed mean where the mean is calculated after a certain percentage (say, 5% or 10%) of the lowest and highest scores in a distribution have been ignored (a process called ‘trimming’; see, for example, the discussion in Field 2018 , pp. 262–264). This yields a statistic less influenced by extreme scores. The drawbacks are that the decision as to what percentage to trim can be somewhat subjective and trimming necessarily sacrifices information (i.e. the extreme scores) in order to achieve a less biased measure. Some software packages, such as SPSS, SYSTAT or NCSS, can report a specific percentage trimmed mean, if that option is selected for descriptive statistics or exploratory data analysis (see Procedure 5.6 ) procedures. Comparing the original mean with a trimmed mean can provide an indication of the degree to which the original mean has been biased by extreme values.
Very simply, the median is the centre or middle score of a set of scores. By ‘centre’ or ‘middle’ is meant that 50% of the data values are smaller than or equal to the median and 50% of the data values are larger when the entire distribution of scores is rank ordered from the lowest to highest value. Thus, we can say that the median is that score in the sample which occurs at the 50th percentile. [Note that a ‘percentile’ is attached to a specific score that a specific percentage of the sample scored at or below. Thus, a score at the 25th percentile means that 25% of the sample achieved this score or a lower score.] Table 5.3 shows the 25th, 50th and 75th percentile scores for each variable – note how the 50th percentile score is exactly equal to the median in each case .
The median is reported somewhat less frequently than the mean but does have some advantages over the mean in certain circumstances. One such circumstance is when the sample of data has a few extreme values in one direction (either very large or very small relative to all other scores). In this case, the mean would be influenced (biased) to a much greater degree than would the median since all of the data are used to calculate the mean (including the extreme scores) whereas only the single centre score is needed for the median. For this reason, many nonparametric statistical procedures (such as Procedures 7.3 , 7.5 and 7.9 ) focus on the median as the comparison statistic rather than on the mean.
A discrepancy between the values for the mean and median of a variable provides some insight to the degree to which the mean is being influenced by the presence of extreme data values. In a distribution where there are no extreme values on either side of the distribution (or where extreme values balance each other out on either side of the distribution, as happens in a normal distribution – see Fundamental Concept II ), the mean and the median will coincide at the same value and the mean will not be biased.
For highly skewed distributions, however, the value of the mean will be pulled toward the long tail of the distribution because that is where the extreme values lie. However, in such skewed distributions, the median will be insensitive (statisticians call this property ‘robustness’) to extreme values in the long tail. For this reason, the direction of the discrepancy between the mean and median can give a very rough indication of the direction of skew in a distribution (‘mean larger than median’ signals possible positive skewness; ‘mean smaller than median’ signals possible negative skewness). Like the mean, there is one and only one possible value for the median in a specific distribution.
In Fig. 5.19 , the left graph shows the distribution of speed scores and the right-hand graph shows the distribution of accuracy scores. The speed distribution clearly shows the mean being pulled toward the right tail of the distribution whereas the accuracy distribution shows the mean being just slightly pulled toward the left tail. The effect on the mean is stronger in the speed distribution indicating a greater biasing effect due to some very long inspection decision times.
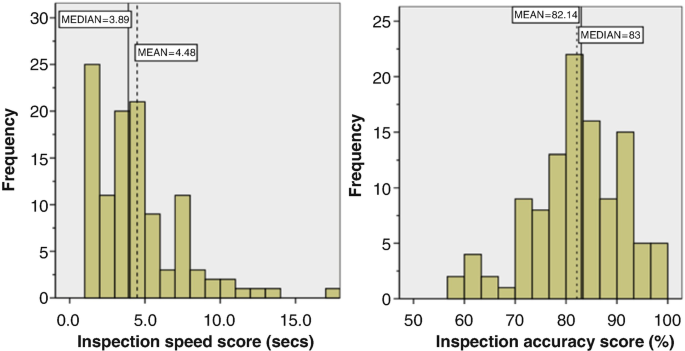
Effects of skewness in a distribution on the values for the mean and median
If we refer to Table 5.3 , we can see that the median score for each of the five variables has also been computed. Like the mean, the median must be interpreted in the original units of measurement for the variable. We can see that for mentabil , accuracy , and workcond , the value of the median is very close to the value of the mean, suggesting that these distributions are not strongly influenced by extreme data values in either the high or low direction. However, note that the median speed was 3.89 s compared to the mean of 4.48 s, suggesting that the distribution of speed scores is positively skewed (the mean is larger than the median—refer to Fig. 5.19 ). Conversely, the median jobsat score was 5.00 whereas the mean score was 4.96 suggesting very little substantive skewness in the distribution (mean and median are nearly equal).
The mode is the simplest measure of central tendency. It is defined as the most frequently occurring score in a distribution. Put another way, it is the score that more individuals in the sample obtain than any other score. An interesting problem associated with the mode is that there may be more than one in a specific distribution. In the case where multiple modes exist, the issue becomes which value do you report? The answer is that you must report all of them. In a ‘normal’ bell-shaped distribution, there is only one mode and it is indeed at the centre of the distribution, coinciding with both the mean and the median.
Table 5.3 also shows the mode for each of the five variables. For example, more inspectors achieved a mentabil score of 111 more often than any other score and inspectors reported a jobsat rating of 6 more often than any other rating. SPSS only ever reports one mode even if several are present, so one must be careful and look at a histogram plot for each variable to make a final determination of the mode(s) for that variable.
All three measures of central tendency yield information about what is going on in the centre of a distribution of scores. The mean and median provide a single number which can summarise the central tendency in the entire distribution. The mode can yield one or multiple indices. With many measurements on individuals in a sample, it is advantageous to have single number indices which can describe the distributions in summary fashion. In a normal or near-normal distribution of sample data, the mean, the median, and the mode will all generally coincide at the one point. In this instance, all three statistics will provide approximately the same indication of central tendency. Note however that it is seldom the case that all three statistics would yield exactly the same number for any particular distribution. The mean is the most useful statistic, unless the data distribution is skewed by extreme scores, in which case the median should be reported.
While measures of central tendency are useful descriptors of distributions, summarising data using a single numerical index necessarily reduces the amount of information available about the sample. Not only do we need to know what is going on in the centre of a distribution, we also need to know what is going on around the centre of the distribution. For this reason, most social and behavioural researchers report not only measures of central tendency, but also measures of variability (see Procedure 5.5 ). The mode is the least informative of the three statistics because of its potential for producing multiple values.
Measures of central tendency are useful in almost any type of experimental design, survey or interview study, and in any observational studies where quantitative data are available and must be summarised. The decision as to whether the mean or median should be reported depends upon the nature of the data which should ideally be ascertained by visual inspection of the data distribution. Some researchers opt to report both measures routinely. Computation of means is a prelude to many parametric statistical methods (see, for example, Procedure 7.2 , 7.4 , 7.6 , 7.8 , 7.10 , 7.11 and 7.16 ); comparison of medians is associated with many nonparametric statistical methods (see, for example, Procedure 7.3 , 7.5 , 7.9 and 7.12 ).
Application | Procedures |
|---|---|
SPSS | then press the ‘ ’ button and choose mean, median and mode. To see trimmed means, you must use the Exploratory Data Analysis procedure; see . |
NCSS | then select the reports and plots that you want to see; make sure you indicate that you want to see the ‘Means Section’ of the Report. If you want to see trimmed means, tick the ‘Trimmed Section’ of the Report. |
SYSTAT | … then select the mean, median and mode (as well as any other statistics you might wish to see). If you want to see trimmed means, tick the ‘Trimmed mean’ section of the dialog box and set the percentage to trim in the box labelled ‘Two-sided’. |
STATGRAPHICS | or then choose the variable(s) you want to describe and select Summary Statistics (you don’t get any options for statistics to report – measures of central tendency and variability are automatically produced). STATGRAPHICS will not report modes and you will need to use and request ‘Percentiles’ in order to see the 50%ile score which will be the median; however, it won’t be labelled as the median. |
Commander | then select the central tendency statistics you want to see. Commander will not produce modes and to see the median, make sure that the ‘Quantiles’ box is ticked – the .5 quantile score (= 50%ile) score is the median; however, it won’t be labelled as the median. |
Procedure 5.5: Assessing Variability
To give an indication of the degree of spread in a sample of scores; that is, how different the scores tend to be from each other with respect to a specific measure of central tendency.
For the variance and standard deviation , interval or ratio-level measures are needed if these measures of variability are to have any interpretable meaning. At least an ordinal-level of measurement is required for the range and interquartile range to be meaningful.
There are a variety of measures of variability to choose from including the range, interquartile range, variance and standard deviation. Each measure reflects a specific way of defining variability in a distribution of scores on a variable and each has its own advantages and disadvantages. Most measures of variability are associated with a specific measure of central tendency so that researchers are now commonly expected to report both a measure of central tendency and its associated measure of variability whenever they display numerical descriptive statistics on continuous or ranked-ordered variables.
This is the simplest measure of variability for a sample of data scores. The range is merely the largest score in the sample minus the smallest score in the sample. The range is the one measure of variability not explicitly associated with any measure of central tendency. It gives a very rough indication as to the extent of spread in the scores. However, since the range uses only two of the total available scores in the sample, the rest of the scores are ignored, which means that a lot of potentially useful information is being sacrificed. There are also problems if either the highest or lowest (or both) scores are atypical or too extreme in their value (as in highly skewed distributions). When this happens, the range gives a very inflated picture of the typical variability in the scores. Thus, the range tends not be a frequently reported measure of variability.
Table 5.4 shows a set of descriptive statistics, produced by the SPSS Frequencies procedure, for the mentabil, accuracy, speed, jobsat and workcond measures in the QCI database. In the table, you will find three rows labelled ‘Range’, ‘Minimum’ and ‘Maximum’.
Using the data from these three rows, we can draw the following descriptive picture. Mentabil scores spanned a range of 50 (from a minimum score of 85 to a maximum score of 135). Speed scores had a range of 16.05 s (from 1.05 s – the fastest quality decision to 17.10 – the slowest quality decision). Accuracy scores had a range of 43 (from 57% – the least accurate inspector to 100% – the most accurate inspector). Both work context measures ( jobsat and workcond ) exhibited a range of 6 – the largest possible range given the 1 to 7 scale of measurement for these two variables.
Interquartile Range
The Interquartile Range ( IQR ) is a measure of variability that is specifically designed to be used in conjunction with the median. The IQR also takes care of the extreme data problem which typically plagues the range measure. The IQR is defined as the range that is covered by the middle 50% of scores in a distribution once the scores have been ranked in order from lowest value to highest value. It is found by locating the value in the distribution at or below which 25% of the sample scored and subtracting this number from the value in the distribution at or below which 75% of the sample scored. The IQR can also be thought of as the range one would compute after the bottom 25% of scores and the top 25% of scores in the distribution have been ‘chopped off’ (or ‘trimmed’ as statisticians call it).
The IQR gives a much more stable picture of the variability of scores and, like the median, is relatively insensitive to the biasing effects of extreme data values. Some behavioural researchers prefer to divide the IQR in half which gives a measure called the Semi-Interquartile Range ( S-IQR ) . The S-IQR can be interpreted as the distance one must travel away from the median, in either direction, to reach the value which separates the top (or bottom) 25% of scores in the distribution from the remaining 75%.
The IQR or S-IQR is typically not produced by descriptive statistics procedures by default in many computer software packages; however, it can usually be requested as an optional statistic to report or it can easily be computed by hand using percentile scores. Both the median and the IQR figure prominently in Exploratory Data Analysis, particularly in the production of boxplots (see Procedure 5.6 ).
Figure 5.20 illustrates the conceptual nature of the IQR and S-IQR compared to that of the range. Assume that 100% of data values are covered by the distribution curve in the figure. It is clear that these three measures would provide very different values for a measure of variability. Your choice would depend on your purpose. If you simply want to signal the overall span of scores between the minimum and maximum, the range is the measure of choice. But if you want to signal the variability around the median, the IQR or S-IQR would be the measure of choice.
How the range, IQR and S-IQR measures of variability conceptually differ
Note: Some behavioural researchers refer to the IQR as the hinge-spread (or H-spread ) because of its use in the production of boxplots:
the 25th percentile data value is referred to as the ‘lower hinge’;
the 75th percentile data value is referred to as the ‘upper hinge’; and
their difference gives the H-spread.
Midspread is another term you may see used as a synonym for interquartile range.
Referring back to Table 5.4 , we can find statistics reported for the median and for the ‘quartiles’ (25th, 50th and 75th percentile scores) for each of the five variables of interest. The ‘quartile’ values are useful for finding the IQR or S-IQR because SPSS does not report these measures directly. The median clearly equals the 50th percentile data value in the table.
If we focus, for example, on the speed variable, we could find its IQR by subtracting the 25th percentile score of 2.19 s from the 75th percentile score of 5.71 s to give a value for the IQR of 3.52 s (the S-IQR would simply be 3.52 divided by 2 or 1.76 s). Thus, we could report that the median decision speed for inspectors was 3.89 s and that the middle 50% of inspectors showed scores spanning a range of 3.52 s. Alternatively, we could report that the median decision speed for inspectors was 3.89 s and that the middle 50% of inspectors showed scores which ranged 1.76 s either side of the median value.
Note: We could compare the ‘Minimum’ or ‘Maximum’ scores to the 25th percentile score and 75th percentile score respectively to get a feeling for whether the minimum or maximum might be considered extreme or uncharacteristic data values.
The variance uses information from every individual in the sample to assess the variability of scores relative to the sample mean. Variance assesses the average squared deviation of each score from the mean of the sample. Deviation refers to the difference between an observed score value and the mean of the sample—they are squared simply because adding them up in their naturally occurring unsquared form (where some differences are positive and others are negative) always gives a total of zero, which is useless for an index purporting to measure something.
If many scores are quite different from the mean, we would expect the variance to be large. If all the scores lie fairly close to the sample mean, we would expect a small variance. If all scores exactly equal the mean (i.e. all the scores in the sample have the same value), then we would expect the variance to be zero.
Figure 5.21 illustrates some possibilities regarding variance of a distribution of scores having a mean of 100. The very tall curve illustrates a distribution with small variance. The distribution of medium height illustrates a distribution with medium variance and the flattest distribution ia a distribution with large variance.
The concept of variance
If we had a distribution with no variance, the curve would simply be a vertical line at a score of 100 (meaning that all scores were equal to the mean). You can see that as variance increases, the tails of the distribution extend further outward and the concentration of scores around the mean decreases. You may have noticed that variance and range (as well as the IQR) will be related, since the range focuses on the difference between the ends of the two tails in the distribution and larger variances extend the tails. So, a larger variance will generally be associated with a larger range and IQR compared to a smaller variance.
It is generally difficult to descriptively interpret the variance measure in a meaningful fashion since it involves squared deviations around the sample mean. [Note: If you look back at Table 5.4 , you will see the variance listed for each of the variables (e.g. the variance of accuracy scores is 84.118), but the numbers themselves make little sense and do not relate to the original measurement scale for the variables (which, for the accuracy variable, went from 0% to 100% accuracy).] Instead, we use the variance as a steppingstone for obtaining a measure of variability that we can clearly interpret, namely the standard deviation . However, you should know that variance is an important concept in its own right simply because it provides the statistical foundation for many of the correlational procedures and statistical inference procedures described in Chaps. 6 , 7 and 8 .
When considering either correlations or tests of statistical hypotheses, we frequently speak of one variable explaining or sharing variance with another (see Procedure 6.4 and 7.7 ). In doing so, we are invoking the concept of variance as set out here—what we are saying is that variability in the behaviour of scores on one particular variable may be associated with or predictive of variability in scores on another variable of interest (e.g. it could explain why those scores have a non-zero variance).
Standard Deviation
The standard deviation (often abbreviated as SD, sd or Std. Dev.) is the most commonly reported measure of variability because it has a meaningful interpretation and is used in conjunction with reports of sample means. Variance and standard deviation are closely related measures in that the standard deviation is found by taking the square root of the variance. The standard deviation, very simply, is a summary number that reflects the ‘average distance of each score from the mean of the sample’. In many parametric statistical methods, both the sample mean and sample standard deviation are employed in some form. Thus, the standard deviation is a very important measure, not only for data description, but also for hypothesis testing and the establishment of relationships as well.
Referring again back to Table 5.4 , we’ll focus on the results for the speed variable for discussion purposes. Table 5.4 shows that the mean inspection speed for the QCI sample was 4.48 s. We can also see that the standard deviation (in the row labelled ‘Std Deviation’) for speed was 2.89 s.
This standard deviation has a straightforward interpretation: we would say that ‘on the average, an inspector’s quality inspection decision speed differed from the mean of the sample by about 2.89 s in either direction’. In a normal distribution of scores (see Fundamental Concept II ), we would expect to see about 68% of all inspectors having decision speeds between 1.59 s (the mean minus one amount of the standard deviation) and 7.37 s (the mean plus one amount of the standard deviation).
We noted earlier that the range of the speed scores was 16.05 s. However, the fact that the maximum speed score was 17.1 s compared to the 75th percentile score of just 5.71 s seems to suggest that this maximum speed might be rather atypically large compared to the bulk of speed scores. This means that the range is likely to be giving us a false impression of the overall variability of the inspectors’ decision speeds.
Furthermore, given that the mean speed score was higher than the median speed score, suggesting that speed scores were positively skewed (this was confirmed by the histogram for speed shown in Fig. 5.19 in Procedure 5.4 ), we might consider emphasising the median and its associated IQR or S-IQR rather than the mean and standard deviation. Of course, similar diagnostic and interpretive work could be done for each of the other four variables in Table 5.4 .
Measures of variability (particularly the standard deviation) provide a summary measure that gives an indication of how variable (spread out) a particular sample of scores is. When used in conjunction with a relevant measure of central tendency (particularly the mean), a reasonable yet economical description of a set of data emerges. When there are extreme data values or severe skewness is present in the data, the IQR (or S-IQR) becomes the preferred measure of variability to be reported in conjunction with the sample median (or 50th percentile value). These latter measures are much more resistant (‘robust’) to influence by data anomalies than are the mean and standard deviation.
As mentioned above, the range is a very cursory index of variability, thus, it is not as useful as variance or standard deviation. Variance has little meaningful interpretation as a descriptive index; hence, standard deviation is most often reported. However, the standard deviation (or IQR) has little meaning if the sample mean (or median) is not reported along with it.
Knowing that the standard deviation for accuracy is 9.17 tells you little unless you know the mean accuracy (82.14) that it is the standard deviation from.
Like the sample mean, the standard deviation can be strongly biased by the presence of extreme data values or severe skewness in a distribution in which case the median and IQR (or S-IQR) become the preferred measures. The biasing effect will be most noticeable in samples which are small in size (say, less than 30 individuals) and far less noticeable in large samples (say, in excess of 200 or 300 individuals). [Note that, in a manner similar to a trimmed mean, it is possible to compute a trimmed standard deviation to reduce the biasing effect of extreme data values, see Field 2018 , p. 263.]
It is important to realise that the resistance of the median and IQR (or S-IQR) to extreme values is only gained by deliberately sacrificing a good deal of the information available in the sample (nothing is obtained without a cost in statistics). What is sacrificed is information from all other members of the sample other than those members who scored at the median and 25th and 75th percentile points on a variable of interest; information from all members of the sample would automatically be incorporated in mean and standard deviation for that variable.
Any investigation where you might report on or read about measures of central tendency on certain variables should also report measures of variability. This is particularly true for data from experiments, quasi-experiments, observational studies and questionnaires. It is important to consider measures of central tendency and measures of variability to be inextricably linked—one should never report one without the other if an adequate descriptive summary of a variable is to be communicated.
Other descriptive measures, such as those for skewness and kurtosis Footnote 1 may also be of interest if a more complete description of any variable is desired. Most good statistical packages can be instructed to report these additional descriptive measures as well.
Of all the statistics you are likely to encounter in the business, behavioural and social science research literature, means and standard deviations will dominate as measures for describing data. Additionally, these statistics will usually be reported when any parametric tests of statistical hypotheses are presented as the mean and standard deviation provide an appropriate basis for summarising and evaluating group differences.
Application | Procedures |
|---|---|
SPSS | then press the ‘ ’ button and choose Std. Deviation, Variance, Range, Minimum and/or Maximum as appropriate. SPSS does not produce or have an option to produce either the IQR or S-IQR, however, if your request ‘Quantiles’ you will see the 25th and 75th %ile scores, which can then be used to quickly compute either variability measure. Remember to select appropriate central tendency measures as well. |
NCSS | then select the reports and plots that you want to see; make sure you indicate that you want to see the Variance Section of the Report. Remember to select appropriate central tendency measures as well (by opting to see the Means Section of the Report). |
SYSTAT | … then select SD, Variance, Range, Interquartile range, Minimum and/or Maximum as appropriate. Remember to select appropriate central tendency measures as well. |
STATGRAPHICS | or then choose the variable(s) you want to describe and select Summary Statistics (you don’t get any options for statistics to report – measures of central tendency and variability are automatically produced). STATGRAPHICS does not produce either the IQR or S-IQR, however, if you use Percentiles’ can be requested in order to see the 25th and 75th %ile scores, which can then be used to quickly compute either variability measure. |
Commander | then select either the Standard Deviation or Interquartile Range as appropriate. Commander will not produce the range statistic or report minimum or maximum scores. Remember to select appropriate central tendency measures as well. |
Fundamental Concept I: Basic Concepts in Probability
The concept of simple probability.
In Procedures 5.1 and 5.2 , you encountered the idea of the frequency of occurrence of specific events such as particular scores within a sample distribution. Furthermore, it is a simple operation to convert the frequency of occurrence of a specific event into a number representing the relative frequency of that event. The relative frequency of an observed event is merely the number of times the event is observed divided by the total number of times one makes an observation. The resulting number ranges between 0 and 1 but we typically re-express this number as a percentage by multiplying it by 100%.
In the QCI database, Maree Lakota observed data from 112 quality control inspectors of which 58 were male and 51 were female (gender indications were missing for three inspectors). The statistics 58 and 51 are thus the frequencies of occurrence for two specific types of research participant, a male inspector or a female inspector.
If she divided each frequency by the total number of observations (i.e. 112), whe would obtain .52 for males and .46 for females (leaving .02 of observations with unknown gender). These statistics are relative frequencies which indicate the proportion of times that Maree obtained data from a male or female inspector. Multiplying each relative frequency by 100% would yield 52% and 46% which she could interpret as indicating that 52% of her sample was male and 46% was female (leaving 2% of the sample with unknown gender).
It does not take much of a leap in logic to move from the concept of ‘relative frequency’ to the concept of ‘probability’. In our discussion above, we focused on relative frequency as indicating the proportion or percentage of times a specific category of participant was obtained in a sample. The emphasis here is on data from a sample.
Imagine now that Maree had infinite resources and research time and was able to obtain ever larger samples of quality control inspectors for her study. She could still compute the relative frequencies for obtaining data from males and females in her sample but as her sample size grew larger and larger, she would notice these relative frequencies converging toward some fixed values.
If, by some miracle, Maree could observe all of the quality control inspectors on the planet today, she would have measured the entire population and her computations of relative frequency for males and females would yield two precise numbers, each indicating the proportion of the population of inspectors that was male and the proportion that was female.
If Maree were then to list all of these inspectors and randomly choose one from the list, the chances that she would choose a male inspector would be equal to the proportion of the population of inspectors that was male and this logic extends to choosing a female inspector. The number used to quantify this notion of ‘chances’ is called a probability. Maree would therefore have established the probability of randomly observing a male or a female inspector in the population on any specific occasion.
Probability is expressed on a 0.0 (the observation or event will certainly not be seen) to 1.0 (the observation or event will certainly be seen) scale where values close to 0.0 indicate observations that are less certain to be seen and values close to 1.0 indicate observations that are more certain to be seen (a value of .5 indicates an even chance that an observation or event will or will not be seen – a state of maximum uncertainty). Statisticians often interpret a probability as the likelihood of observing an event or type of individual in the population.
In the QCI database, we noted that the relative frequency of observing males was .52 and for females was .46. If we take these relative frequencies as estimates of the proportions of each gender in the population of inspectors, then .52 and .46 represent the probability of observing a male or female inspector, respectively.
Statisticians would state this as “the probability of observing a male quality control inspector is .52” or in a more commonly used shorthand code, the likelihood of observing a male quality control inspector is p = .52 (p for probability). For some, probabilities make more sense if they are converted to percentages (by multiplying by 100%). Thus, p = .52 can also understood as a 52% chance of observing a male quality control inspector.
We have seen that relative frequency is a sample statistic that can be used to estimate the population probability. Our estimate will get more precise as we use larger and larger samples (technically, as the size of our samples more closely approximates the size of our population). In most behavioural research, we never have access to entire populations so we must always estimate our probabilities.
In some very special populations, having a known number of fixed possible outcomes, such as results of coin tosses or rolls of a die, we can analytically establish event probabilities without doing an infinite number of observations; all we must do is assume that we have a fair coin or die. Thus, with a fair coin, the probability of observing a H or a T on any single coin toss is ½ or .5 or 50%; the probability of observing a 6 on any single throw of a die is 1/6 or .16667 or 16.667%. With behavioural data, though, we can never measure all possible behavioural outcomes, which thereby forces researchers to depend on samples of observations in order to make estimates of population values.
The concept of probability is central to much of what is done in the statistical analysis of behavioural data. Whenever a behavioural scientist wishes to establish whether a particular relationship exists between variables or whether two groups, treated differently, actually show different behaviours, he/she is playing a probability game. Given a sample of observations, the behavioural scientist must decide whether what he/she has observed is providing sufficient information to conclude something about the population from which the sample was drawn.
This decision always has a non-zero probability of being in error simply because in samples that are much smaller than the population, there is always the chance or probability that we are observing something rare and atypical instead of something which is indicative of a consistent population trend. Thus, the concept of probability forms the cornerstone for statistical inference about which we will have more to say later (see Fundamental Concept VI ). Probability also plays an important role in helping us to understand theoretical statistical distributions (e.g. the normal distribution) and what they can tell us about our observations. We will explore this idea further in Fundamental Concept II .
The Concept of Conditional Probability
It is important to understand that the concept of probability as described above focuses upon the likelihood or chances of observing a specific event or type of observation for a specific variable relative to a population or sample of observations. However, many important behavioural research issues may focus on the question of the probability of observing a specific event given that the researcher has knowledge that some other event has occurred or been observed (this latter event is usually measured by a second variable). Here, the focus is on the potential relationship or link between two variables or two events.
With respect to the QCI database, Maree could ask the quite reasonable question “what is the probability (estimated in the QCI sample by a relative frequency) of observing an inspector being female given that she knows that an inspector works for a Large Business Computer manufacturer.
To address this question, all she needs to know is:
how many inspectors from Large Business Computer manufacturers are in the sample ( 22 ); and
how many of those inspectors were female ( 7 ) (inspectors who were missing a score for either company or gender have been ignored here).
If she divides 7 by 22, she would obtain the probability that an inspector is female given that they work for a Large Business Computer manufacturer – that is, p = .32 .
This type of question points to the important concept of conditional probability (‘conditional’ because we are asking “what is the probability of observing one event conditional upon our knowledge of some other event”).
Continuing with the previous example, Maree would say that the conditional probability of observing a female inspector working for a Large Business Computer manufacturer is .32 or, equivalently, a 32% chance. Compare this conditional probability of p = .32 to the overall probability of observing a female inspector in the entire sample ( p = .46 as shown above).
This means that there is evidence for a connection or relationship between gender and the type of company an inspector works for. That is, the chances are lower for observing a female inspector from a Large Business Computer manufacturer than they are for simply observing a female inspector at all.
Maree therefore has evidence suggesting that females may be relatively under-represented in Large Business Computer manufacturing companies compared to the overall population. Knowing something about the company an inspector works for therefore can help us make a better prediction about their likely gender.
Suppose, however, that Maree’s conditional probability had been exactly equal to p = .46. This would mean that there was exactly the same chance of observing a female inspector working for a Large Business Computer manufacturer as there was of observing a female inspector in the general population. Here, knowing something about the company an inspector works doesn’t help Maree make any better prediction about their likely gender. This would mean that the two variables are statistically independent of each other.
A classic case of events that are statistically independent is two successive throws of a fair die: rolling a six on the first throw gives us no information for predicting how likely it will be that we would roll a six on the second throw. The conditional probability of observing a six on the second throw given that I have observed a six on the first throw is 0.16667 (= 1 divided by 6) which is the same as the simple probability of observing a six on any specific throw. This statistical independence also means that if we wanted to know what the probability of throwing two sixes on two successive throws of a fair die, we would just multiply the probabilities for each independent event (i.e., throw) together; that is, .16667 × .16667 = .02789 (this is known as the multiplication rule of probability, see, for example, Smithson 2000 , p. 114).
Finally, you should know that conditional probabilities are often asymmetric. This means that for many types of behavioural variables, reversing the conditional arrangement will change the story about the relationship. Bayesian statistics (see Fundamental Concept IX ) relies heavily upon this asymmetric relationship between conditional probabilities.
Maree has already learned that the conditional probability that an inspector is female given that they worked for a Large Business Computer manufacturer is p = .32. She could easily turn the conditional relationship around and ask what is the conditional probability that an inspector works for a Large Business Computer manufacturer given that the inspector is female?
From the QCI database, she can find that 51 inspectors in her total sample were female and of those 51, 7 worked for a Large Business Computer manufacturer. If she divided 7 by 51, she would get p = .14 (did you notice that all that changed was the number she divided by?). Thus, there is only a 14% chance of observing an inspector working for a Large Business Computer manufacturer given that the inspector is female – a rather different probability from p = .32, which tells a different story.
As you will see in Procedures 6.2 and 7.1 , conditional relationships between categorical variables are precisely what crosstabulation contingency tables are designed to reveal.
Procedure 5.6: Exploratory Data Analysis
To visually summarise data, displaying some key characteristics of their distribution, while maintaining as much of their original integrity as possible.
Exploratory Data Analysis (EDA) procedures are most usefully employed to explore data measured at the ordinal, interval or ratio-level.
There are a variety of visual display methods for EDA, including stem & leaf displays, boxplots and violin plots. Each method reflects a specific way of displaying features of a distribution of scores or measurements and, of course, each has its own advantages and disadvantages. In addition, EDA displays are surprisingly flexible and can combine features in various ways to enhance the story conveyed by the plot.
Stem & Leaf Displays
The stem & leaf display is a simple data summary technique which not only rank orders the data points in a sample but presents them visually so that the shape of the data distribution is reflected. Stem & leaf displays are formed from data scores by splitting each score into two parts: the first part of each score serving as the ‘stem’, the second part as the ‘leaf’ (e.g. for 2-digit data values, the ‘stem’ is the number in the tens position; the ‘leaf’ is the number in the ones position). Each stem is then listed vertically, in ascending order, followed horizontally by all the leaves in ascending order associated with it. The resulting display thus shows all of the scores in the sample, but reorganised so that a rough idea of the shape of the distribution emerges. As well, extreme scores can be easily identified in a stem & leaf display.
Consider the accuracy and speed scores for the 112 quality control inspectors in the QCI sample. Figure 5.22 (produced by the R Commander Stem-and-leaf display … procedure) shows the stem & leaf displays for inspection accuracy (left display) and speed (right display) data.
Stem & leaf displays produced by R Commander
[The first six lines reflect information from R Commander about each display: lines 1 and 2 show the actual R command used to produce the plot (the variable name has been highlighted in bold); line 3 gives a warning indicating that inspectors with missing values (= NA in R ) on the variable have been omitted from the display; line 4 shows how the stems and leaves have been defined; line 5 indicates what a leaf unit represents in value; and line 6 indicates the total number (n) of inspectors included in the display).] In Fig. 5.22 , for the accuracy display on the left-hand side, the ‘stems’ have been split into ‘half-stems’—one (which is starred) associated with the ‘leaves’ 0 through 4 and the other associated with the ‘leaves’ 5 through 9—a strategy that gives the display better balance and visual appeal.
Notice how the left stem & leaf display conveys a fairly clear (yet sideways) picture of the shape of the distribution of accuracy scores. It has a rather symmetrical bell-shape to it with only a slight suggestion of negative skewness (toward the extreme score at the top). The right stem & leaf display clearly depicts the highly positively skewed nature of the distribution of speed scores. Importantly, we could reconstruct the entire sample of scores for each variable using its display, which means that unlike most other graphical procedures, we didn’t have to sacrifice any information to produce the visual summary.
Some programs, such as SYSTAT, embellish their stem & leaf displays by indicating in which stem or half-stem the ‘median’ (50th percentile), the ‘upper hinge score’ (75th percentile), and ‘lower hinge score’ (25th percentile) occur in the distribution (recall the discussion of interquartile range in Procedure 5.5 ). This is shown in Fig. 5.23 , produced by SYSTAT, where M and H indicate the stem locations for the median and hinge points, respectively. This stem & leaf display labels a single extreme accuracy score as an ‘outside value’ and clearly shows that this actual score was 57.
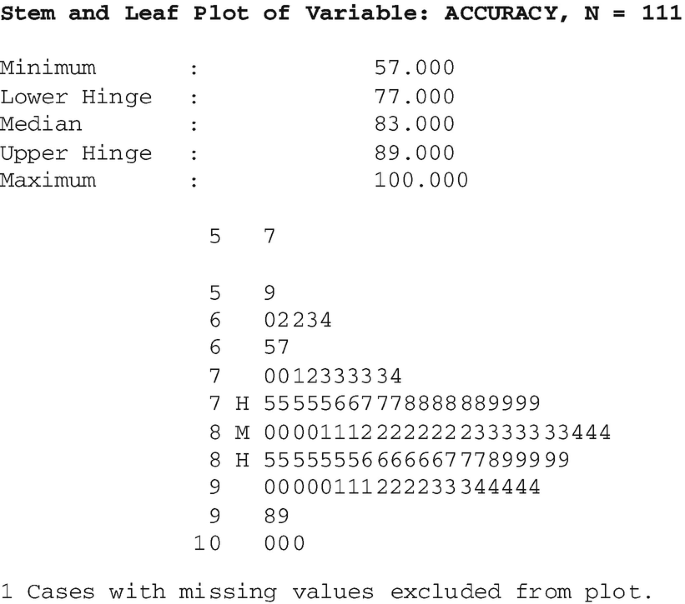
Stem & leaf display, produced by SYSTAT, of the accuracy QCI variable
Another important EDA technique is the boxplot or, as it is sometimes known, the box-and-whisker plot . This plot provides a symbolic representation that preserves less of the original nature of the data (compared to a stem & leaf display) but typically gives a better picture of the distributional characteristics. The basic boxplot, shown in Fig. 5.24 , utilises information about the median (50th percentile score) and the upper (75th percentile score) and lower (25th percentile score) hinge points in the construction of the ‘box’ portion of the graph (the ‘median’ defines the centre line in the box; the ‘upper’ and ‘lower hinge values’ define the end boundaries of the box—thus the box encompasses the middle 50% of data values).
Boxplots for the accuracy and speed QCI variables
Additionally, the boxplot utilises the IQR (recall Procedure 5.5 ) as a way of defining what are called ‘fences’ which are used to indicate score boundaries beyond which we would consider a score in a distribution to be an ‘outlier’ (or an extreme or unusual value). In SPSS, the inner fence is typically defined as 1.5 times the IQR in each direction and a ‘far’ outlier or extreme case is typically defined as 3 times the IQR in either direction (Field 2018 , p. 193). The ‘whiskers’ in a boxplot extend out to the data values which are closest to the upper and lower inner fences (in most cases, the vast majority of data values will be contained within the fences). Outliers beyond these ‘whiskers’ are then individually listed. ‘Near’ outliers are those lying just beyond the inner fences and ‘far’ outliers lie well beyond the inner fences.
Figure 5.24 shows two simple boxplots (produced using SPSS), one for the accuracy QCI variable and one for the speed QCI variable. The accuracy plot shows a median value of about 83, roughly 50% of the data fall between about 77 and 89 and there is one outlier, inspector 83, in the lower ‘tail’ of the distribution. The accuracy boxplot illustrates data that are relatively symmetrically distributed without substantial skewness. Such data will tend to have their median in the middle of the box, whiskers of roughly equal length extending out from the box and few or no outliers.
The speed plot shows a median value of about 4 s, roughly 50% of the data fall between 2 s and 6 s and there are four outliers, inspectors 7, 62, 65 and 75 (although inspectors 65 and 75 fall at the same place and are rather difficult to read), all falling in the slow speed ‘tail’ of the distribution. Inspectors 65, 75 and 7 are shown as ‘near’ outliers (open circles) whereas inspector 62 is shown as a ‘far’ outlier (asterisk). The speed boxplot illustrates data which are asymmetrically distributed because of skewness in one direction. Such data may have their median offset from the middle of the box and/or whiskers of unequal length extending out from the box and outliers in the direction of the longer whisker. In the speed boxplot, the data are clearly positively skewed (the longer whisker and extreme values are in the slow speed ‘tail’).
Boxplots are very versatile representations in that side-by-side displays for sub-groups of data within a sample can permit easy visual comparisons of groups with respect to central tendency and variability. Boxplots can also be modified to incorporate information about error bands associated with the median producing what is called a ‘notched boxplot’. This helps in the visual detection of meaningful subgroup differences, where boxplot ‘notches’ don’t overlap.
Figure 5.25 (produced using NCSS), compares the distributions of accuracy and speed scores for QCI inspectors from the five types of companies, plotted side-by-side.
Comparisons of the accuracy (regular boxplots) and speed (notched boxplots) QCI variables for different types of companies
Focus first on the left graph in Fig. 5.25 which plots the distribution of accuracy scores broken down by company using regular boxplots. This plot clearly shows the differing degree of skewness in each type of company (indicated by one or more outliers in one ‘tail’, whiskers which are not the same length and/or the median line being offset from the centre of a box), the differing variability of scores within each type of company (indicated by the overall length of each plot—box and whiskers), and the differing central tendency in each type of company (the median lines do not all fall at the same level of accuracy score). From the left graph in Fig. 5.25 , we could conclude that: inspection accuracy scores are most variable in PC and Large Electrical Appliance manufacturing companies and least variable in the Large Business Computer manufacturing companies; Large Business Computer and PC manufacturing companies have the highest median level of inspection accuracy; and inspection accuracy scores tend to be negatively skewed (many inspectors toward higher levels, relatively fewer who are poorer in inspection performance) in the Automotive manufacturing companies. One inspector, working for an Automotive manufacturing company, shows extremely poor inspection accuracy performance.
The right display compares types of companies in terms of their inspection speed scores, using’ notched’ boxplots. The notches define upper and lower error limits around each median. Aside from the very obvious positive skewness for speed scores (with a number of slow speed outliers) in every type of company (least so for Large Electrical Appliance manufacturing companies), the story conveyed by this comparison is that inspectors from Large Electrical Appliance and Automotive manufacturing companies have substantially faster median decision speeds compared to inspectors from Large Business Computer and PC manufacturing companies (i.e. their ‘notches’ do not overlap, in terms of speed scores, on the display).
Boxplots can also add interpretive value to other graphical display methods through the creation of hybrid displays. Such displays might combine a standard histogram with a boxplot along the X-axis to provide an enhanced picture of the data distribution as illustrated for the mentabil variable in Fig. 5.26 (produced using NCSS). This hybrid plot also employs a data ‘smoothing’ method called a density trace to outline an approximate overall shape for the data distribution. Any one graphical method would tell some of the story, but combined in the hybrid display, the story of a relatively symmetrical set of mentabil scores becomes quite visually compelling.
A hybrid histogram-density-boxplot of the mentabil QCI variable
Violin Plots
Violin plots are a more recent and interesting EDA innovation, implemented in the NCSS software package (Hintze 2012 ). The violin plot gets its name from the rough shape that the plots tend to take on. Violin plots are another type of hybrid plot, this time combining density traces (mirror-imaged right and left so that the plots have a sense of symmetry and visual balance) with boxplot-type information (median, IQR and upper and lower inner ‘fences’, but not outliers). The goal of the violin plot is to provide a quick visual impression of the shape, central tendency and variability of a distribution (the length of the violin conveys a sense of the overall variability whereas the width of the violin conveys a sense of the frequency of scores occurring in a specific region).
Figure 5.27 (produced using NCSS), compares the distributions of speed scores for QCI inspectors across the five types of companies, plotted side-by-side. The violin plot conveys a similar story to the boxplot comparison for speed in the right graph of Fig. 5.25 . However, notice that with the violin plot, unlike with a boxplot, you also get a sense of distributions that have ‘clumps’ of scores in specific areas. Some violin plots, like that for Automobile manufacturing companies in Fig. 5.27 , have a shape suggesting a multi-modal distribution (recall Procedure 5.4 and the discussion of the fact that a distribution may have multiple modes). The violin plot in Fig. 5.27 has also been produced to show where the median (solid line) and mean (dashed line) would fall within each violin. This facilitates two interpretations: (1) a relative comparison of central tendency across the five companies and (2) relative degree of skewness in the distribution for each company (indicated by the separation of the two lines within a violin; skewness is particularly bad for the Large Business Computer manufacturing companies).
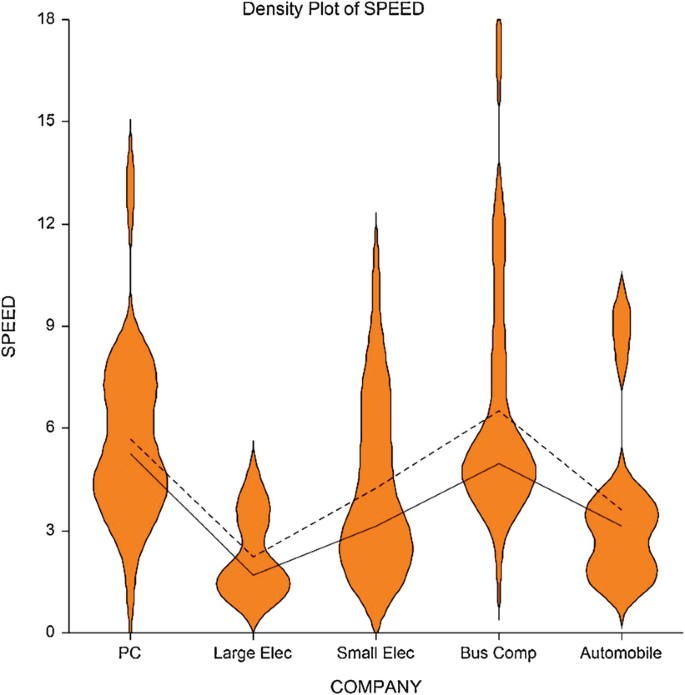
Violin plot comparisons of the speed QCI variable for different types of companies
EDA methods (of which we have illustrated only a small subset; we have not reviewed dot density diagrams, for example) provide summary techniques for visually displaying certain characteristics of a set of data. The advantage of the EDA methods over more traditional graphing techniques such as those described in Procedure 5.2 is that as much of the original integrity of the data is maintained as possible while maximising the amount of summary information available about distributional characteristics.
Stem & leaf displays maintain the data in as close to their original form as possible whereas boxplots and violin plots provide more symbolic and flexible representations. EDA methods are best thought of as communication devices designed to facilitate quick visual impressions and they can add interest to any statistical story being conveyed about a sample of data. NCSS, SYSTAT, STATGRAPHICS and R Commander generally offer more options and flexibility in the generation of EDA displays than SPSS.
EDA methods tend to get cumbersome if a great many variables or groups need to be summarised. In such cases, using numerical summary statistics (such as means and standard deviations) will provide a more economical and efficient summary. Boxplots or violin plots are generally more space efficient summary techniques than stem & leaf displays.
Often, EDA techniques are used as data screening devices, which are typically not reported in actual write-ups of research (we will discuss data screening in more detail in Procedure 8.2 ). This is a perfectly legitimate use for the methods although there is an argument for researchers to put these techniques to greater use in published literature.
Software packages may use different rules for constructing EDA plots which means that you might get rather different looking plots and different information from different programs (you saw some evidence of this in Figs. 5.22 and 5.23 ). It is important to understand what the programs are using as decision rules for locating fences and outliers so that you are clear on how best to interpret the resulting plot—such information is generally contained in the user’s guides or manuals for NCSS (Hintze 2012 ), SYSTAT (SYSTAT Inc. 2009a , b ), STATGRAPHICS (StatPoint Technologies Inc. 2010 ) and SPSS (Norušis 2012 ).
Virtually any research design which produces numerical measures (even to the extent of just counting the number of occurrences of several events) provides opportunities for employing EDA displays which may help to clarify data characteristics or relationships. One extremely important use of EDA methods is as data screening devices for detecting outliers and other data anomalies, such as non-normality and skewness, before proceeding to parametric statistical analyses. In some cases, EDA methods can help the researcher to decide whether parametric or nonparametric statistical tests would be best to apply to his or her data because critical data characteristics such as distributional shape and spread are directly reflected.
Application | Procedures |
|---|---|
SPSS | produces stem-and-leaf displays and boxplots by default; variables may be explored on a whole-of-sample basis or broken down by the categories of a specific variable (called a ‘factor’ in the procedure). Cases can also be labelled with a variable (like in the QCI database), so that outlier points in the boxplot are identifiable. can also be used to custom build different types of boxplots. |
NCSS | produces a stem-and-leaf display by default. can be used to produce box plots with different features (such as ‘notches’ and connecting lines). can be configured to produce violin plots (by selecting the plot shape as ‘density with reflection’). |
SYSTAT | can be used to produce stem-and-leaf displays for variables; however, you cannot really control any features of these displays. can be used to produce boxplots of many types, with a number of features being controllable. |
STATGRAPHICS | allows you to do a complete exploration of a single variable, including stem-and-leaf display (you need to select this option) and boxplot (produced by default). Some features of the boxplot can be controlled, but not features of the stem-and-leaf diagram. and select either or which can produce not only descriptive statistics but also boxplots with some controllable features. |
Commander | or the dialog box for each procedure offers some features of the display or plot that can be controlled; whole-of-sample boxplots or boxplots by groups are possible. |
Procedure 5.7: Standard ( z ) Scores
To transform raw scores from a sample of data to a standardised form which permits comparisons with other scores within the same sample or with scores from other samples of data.
Generally, standard scores are computed from interval or ratio-level data.
In certain practical situations in behavioural research, it may be desirable to know where a specific individual’s score lies relative to all other scores in a distribution. A convenient measure is to observe how many standard deviations (see Procedure 5.5 ) above or below the sample mean a specific score lies. This measure is called a standard score or z -score . Very simply, any raw score can be converted to a z -score by subtracting the sample mean from the raw score and dividing that result by the sample’s standard deviation. z -scores can be positive or negative and their sign simply indicates whether the score lies above (+) or below (−) the mean in value. A z -score has a very simple interpretation: it measures the number of standard deviations above or below the sample mean a specific raw score lies.
In the QCI database, we have a sample mean for speed scores of 4.48 s, a standard deviation for speed scores of 2.89 s (recall Table 5.4 in Procedure 5.5 ). If we are interested in the z -score for Inspector 65’s raw speed score of 11.94 s, we would obtain a z -score of +2.58 using the method described above (subtract 4.48 from 11.94 and divide the result by 2.89). The interpretation of this number is that a raw decision speed score of 11.94 s lies about 2.9 standard deviations above the mean decision speed for the sample.
z -scores have some interesting properties. First, if one converts (statisticians would say ‘transforms’) every available raw score in a sample to z -scores, the mean of these z -scores will always be zero and the standard deviation of these z -scores will always be 1.0. These two facts about z -scores (mean = 0; standard deviation = 1) will be true no matter what sample you are dealing with and no matter what the original units of measurement are (e.g. seconds, percentages, number of widgets assembled, amount of preference for a product, attitude rating, amount of money spent). This is because transforming raw scores to z -scores automatically changes the measurement units from whatever they originally were to a new system of measurements expressed in standard deviation units.
Suppose Maree was interested in the performance statistics for the top 25% most accurate quality control inspectors in the sample. Given a sample size of 112, this would mean finding the top 28 inspectors in terms of their accuracy scores. Since Maree is interested in performance statistics, speed scores would also be of interest. Table 5.5 (generated using the SPSS Descriptives … procedure, listed using the Case Summaries … procedure and formatted for presentation using Excel) shows accuracy and speed scores for the top 28 inspectors in descending order of accuracy scores. The z -score transformation for each of these scores is also shown (last two columns) as are the type of company, education level and gender for each inspector.
There are three inspectors (8, 9 and 14) who scored maximum accuracy of 100%. Such accuracy converts to a z -score of +1.95. Thus 100% accuracy is 1.95 standard deviations above the sample’s mean accuracy level. Interestingly, all three inspectors worked for PC manufacturers and all three had only high school-level education. The least accurate inspector in the top 25% had a z -score for accuracy that was .75 standard deviations above the sample mean.
Interestingly, the top three inspectors in terms of accuracy had decision speeds that fell below the sample’s mean speed; inspector 8 was the fastest inspector of the three with a speed just over 1 standard deviation ( z = −1.03) below the sample mean. The slowest inspector in the top 25% was inspector 75 (case #28 in the list) with a speed z -score of +2.62; i.e., he was over two and a half standard deviations slower in making inspection decisions relative to the sample’s mean speed.
The fact that z -scores always have a common measurement scale having a mean of 0 and a standard deviation of 1.0 leads to an interesting application of standard scores. Suppose we focus on inspector number 65 (case #8 in the list) in Table 5.5 . It might be of interest to compare this inspector’s quality control performance in terms of both his decision accuracy and decision speed. Such a comparison is impossible using raw scores since the inspector’s accuracy score and speed scores are different measures which have differing means and standard deviations expressed in fundamentally different units of measurement (percentages and seconds). However, if we are willing to assume that the score distributions for both variables are approximately the same shape and that both accuracy and speed are measured with about the same level of reliability or consistency (see Procedure 8.1 ), we can compare the inspector’s two scores by first converting them to z -scores within their own respective distributions as shown in Table 5.5 .
Inspector 65 looks rather anomalous in that he demonstrated a relatively high level of accuracy (raw score = 94%; z = +1.29) but took a very long time to make those accurate decisions (raw score = 11.94 s; z = +2.58). Contrast this with inspector 106 (case #17 in the list) who demonstrated a similar level of accuracy (raw score = 92%; z = +1.08) but took a much shorter time to make those accurate decisions (raw score = 1.70 s; z = −.96). In terms of evaluating performance, from a company perspective, we might conclude that inspector 106 is performing at an overall higher level than inspector 65 because he can achieve a very high level of accuracy but much more quickly; accurate and fast is more cost effective and efficient than accurate and slow.
Note: We should be cautious here since we know from our previous explorations of the speed variable in Procedure 5.6 , that accuracy scores look fairly symmetrical and speed scores are positively skewed, so assuming that the two variables have the same distribution shape, so that z -score comparisons are permitted, would be problematic.
You might have noticed that as you scanned down the two columns of z -scores in Table 5.5 , there was a suggestion of a pattern between the signs attached to the respective z -scores for each person. There seems to be a very slight preponderance of pairs of z -scores where the signs are reversed (12 out of 22 pairs). This observation provides some very preliminary evidence to suggest that there may be a relationship between inspection accuracy and decision speed, namely that a more accurate decision tends to be associated with a faster decision speed. Of course, this pattern would be better verified using the entire sample rather than the top 25% of inspectors. However, you may find it interesting to learn that it is precisely this sort of suggestive evidence (about agreement or disagreement between z -score signs for pairs of variable scores throughout a sample) that is captured and summarised by a single statistical indicator called a ‘correlation coefficient’ (see Fundamental Concept III and Procedure 6.1 ).
z -scores are not the only type of standard score that is commonly used. Three other types of standard scores are: stanines (standard nines), IQ scores and T-scores (not to be confused with the t -test described in Procedure 7.2 ). These other types of scores have the advantage of producing only positive integer scores rather than positive and negative decimal scores. This makes interpretation somewhat easier for certain applications. However, you should know that almost all other types of standard scores come from a specific transformation of z -scores. This is because once you have converted raw scores into z -scores, they can then be quite readily transformed into any other system of measurement by simply multiplying a person’s z -score by the new desired standard deviation for the measure and adding to that product the new desired mean for the measure.
T-scores are simply z-scores transformed to have a mean of 50.0 and a standard deviation of 10.0; IQ scores are simply z-scores transformed to have a mean of 100 and a standard deviation of 15 (or 16 in some systems). For more information, see Fundamental Concept II .
Standard scores are useful for representing the position of each raw score within a sample distribution relative to the mean of that distribution. The unit of measurement becomes the number of standard deviations a specific score is away from the sample mean. As such, z -scores can permit cautious comparisons across samples or across different variables having vastly differing means and standard deviations within the constraints of the comparison samples having similarly shaped distributions and roughly equivalent levels of measurement reliability. z -scores also form the basis for establishing the degree of correlation between two variables. Transforming raw scores into z -scores does not change the shape of a distribution or rank ordering of individuals within that distribution. For this reason, a z -score is referred to as a linear transformation of a raw score. Interestingly, z -scores provide an important foundational element for more complex analytical procedures such as factor analysis ( Procedure 6.5 ), cluster analysis ( Procedure 6.6 ) and multiple regression analysis (see, for example, Procedure 6.4 and 7.13 ).
While standard scores are useful indices, they are subject to restrictions if used to compare scores across samples or across different variables. The samples must have similar distribution shapes for the comparisons to be meaningful and the measures must have similar levels of reliability in each sample. The groups used to generate the z -scores should also be similar in composition (with respect to age, gender distribution, and so on). Because z -scores are not an intuitively meaningful way of presenting scores to lay-persons, many other types of standard score schemes have been devised to improve interpretability. However, most of these schemes produce scores that run a greater risk of facilitating lay-person misinterpretations simply because their connection with z -scores is hidden or because the resulting numbers ‘look’ like a more familiar type of score which people do intuitively understand.
It is extremely rare for a T-score to exceed 100 or go below 0 because this would mean that the raw score was in excess of 5 standard deviations away from the sample mean. This unfortunately means that T-scores are often misinterpreted as percentages because they typically range between 0 and 100 and therefore ‘look’ like percentages. However, T-scores are definitely not percentages.
Finally, a common misunderstanding of z -scores is that transforming raw scores into z -scores makes them follow a normal distribution (see Fundamental Concept II ). This is not the case. The distribution of z -scores will have exactly the same shape as that for the raw scores; if the raw scores are positively skewed, then the corresponding z -scores will also be positively skewed.
z -scores are particularly useful in evaluative studies where relative performance indices are of interest. Whenever you compute a correlation coefficient ( Procedure 6.1 ), you are implicitly transforming the two variables involved into z -scores (which equates the variables in terms of mean and standard deviation), so that only the patterning in the relationship between the variables is represented. z -scores are also useful as a preliminary step to more advanced parametric statistical methods when variables differing in scale, range and/or measurement units must be equated for means and standard deviations prior to analysis.
Application | Procedures |
|---|---|
SPSS | and tick the box labelled ‘Save standardized values as variables’. -scores are saved as new variables (labelled as Z followed by the original variable name as shown in Table ) which can then be listed or analysed further. |
NCSS | and select a new variable to hold the -scores, then select the ‘STANDARDIZE’ transformation from the list of available functions. -scores are saved as new variables which can then be listed or analysed further. |
SYSTAT | where -scores are saved as new variables which can then be listed or analysed further. |
STATGRAPHICS | Open the window, and select an empty column in the database, then and choose the ‘STANDARDIZE’ transformation, choose the variable you want to transform and give the new variable a name. |
Commander | and select the variables you want to standardize; Commander automatically saves the transformed variable to the data base, appending Z. to the front of each variable’s name. |
Fundamental Concept II: The Normal Distribution
Arguably the most fundamental distribution used in the statistical analysis of quantitative data in the behavioural and social sciences is the normal distribution (also known as the Gaussian or bell-shaped distribution ). Many behavioural phenomena, if measured on a large enough sample of people, tend to produce ‘normally distributed’ variable scores. This includes most measures of ability, performance and productivity, personality characteristics and attitudes. The normal distribution is important because it is the one form of distribution that you must assume describes the scores of a variable in the population when parametric tests of statistical inference are undertaken. The standard normal distribution is defined as having a population mean of 0.0 and a population standard deviation of 1.0. The normal distribution is also important as a means of interpreting various types of scoring systems.
Figure 5.28 displays the standard normal distribution (mean = 0; standard deviation = 1.0) and shows that there is a clear link between z -scores and the normal distribution. Statisticians have analytically calculated the probability (also expressed as percentages or percentiles) that observations will fall above or below any specific z -score in the theoretical standard normal distribution. Thus, a z -score of +1.0 in the standard normal distribution will have 84.13% (equals a probability of .8413) of observations in the population falling at or below one standard deviation above the mean and 15.87% falling above that point. A z -score of −2.0 will have 2.28% of observations falling at that point or below and 97.72% of observations falling above that point. It is clear then that, in a standard normal distribution, z -scores have a direct relationship with percentiles .
The normal (bell-shaped or Gaussian) distribution
Figure 5.28 also shows how T-scores relate to the standard normal distribution and to z -scores. The mean T-score falls at 50 and each increment or decrement of 10 T-score units means a movement of another standard deviation away from this mean of 50. Thus, a T-score of 80 corresponds to a z -score of +3.0—a score 3 standard deviations higher than the mean of 50.
Of special interest to behavioural researchers are the values for z -scores in a standard normal distribution that encompass 90% of observations ( z = ±1.645—isolating 5% of the distribution in each tail), 95% of observations ( z = ±1.96—isolating 2.5% of the distribution in each tail), and 99% of observations ( z = ±2.58—isolating 0.5% of the distribution in each tail).
Depending upon the degree of certainty required by the researcher, these bands describe regions outside of which one might define an observation as being atypical or as perhaps not belonging to a distribution being centred at a mean of 0.0. Most often, what is taken as atypical or rare in the standard normal distribution is a score at least two standard deviations away from the mean, in either direction. Why choose two standard deviations? Since in the standard normal distribution, only about 5% of observations will fall outside a band defined by z -scores of ±1.96 (rounded to 2 for simplicity), this equates to data values that are 2 standard deviations away from their mean. This can give us a defensible way to identify outliers or extreme values in a distribution.
Thinking ahead to what you will encounter in Chap. 7 , this ‘banding’ logic can be extended into the world of statistics (like means and percentages) as opposed to just the world of observations. You will frequently hear researchers speak of some statistic estimating a specific value (a parameter ) in a population, plus or minus some other value.
A survey organisation might report political polling results in terms of a percentage and an error band, e.g. 59% of Australians indicated that they would vote Labour at the next federal election, plus or minus 2%.
Most commonly, this error band (±2%) is defined by possible values for the population parameter that are about two standard deviations (or two standard errors—a concept discussed further in Fundamental Concept VIII ) away from the reported or estimated statistical value. In effect, the researcher is saying that on 95% of the occasions he/she would theoretically conduct his/her study, the population value estimated by the statistic being reported would fall between the limits imposed by the endpoints of the error band (the official name for this error band is a confidence interval ; see Procedure 8.3 ). The well-understood mathematical properties of the standard normal distribution are what make such precise statements about levels of error in statistical estimates possible.
Checking for Normality
It is important to understand that transforming the raw scores for a variable to z -scores (recall Procedure 5.7 ) does not produce z -scores which follow a normal distribution; rather they will have the same distributional shape as the original scores. However, if you are willing to assume that the normal distribution is the correct reference distribution in the population, then you are justified is interpreting z -scores in light of the known characteristics of the normal distribution.
In order to justify this assumption, not only to enhance the interpretability of z -scores but more generally to enhance the integrity of parametric statistical analyses, it is helpful to actually look at the sample frequency distributions for variables (using a histogram (illustrated in Procedure 5.2 ) or a boxplot (illustrated in Procedure 5.6 ), for example), since non-normality can often be visually detected. It is important to note that in the social and behavioural sciences as well as in economics and finance, certain variables tend to be non-normal by their very nature. This includes variables that measure time taken to complete a task, achieve a goal or make decisions and variables that measure, for example, income, occurrence of rare or extreme events or organisational size. Such variables tend to be positively skewed in the population, a pattern that can often be confirmed by graphing the distribution.
If you cannot justify an assumption of ‘normality’, you may be able to force the data to be normally distributed by using what is called a ‘normalising transformation’. Such transformations will usually involve a nonlinear mathematical conversion (such as computing the logarithm, square root or reciprocal) of the raw scores. Such transformations will force the data to take on a more normal appearance so that the assumption of ‘normality’ can be reasonably justified, but at the cost of creating a new variable whose units of measurement and interpretation are more complicated. [For some non-normal variables, such as the occurrence of rare, extreme or catastrophic events (e.g. a 100-year flood or forest fire, coronavirus pandemic, the Global Financial Crisis or other type of financial crisis, man-made or natural disaster), the distributions cannot be ‘normalised’. In such cases, the researcher needs to model the distribution as it stands. For such events, extreme value theory (e.g. see Diebold et al. 2000 ) has proven very useful in recent years. This theory uses a variation of the Pareto or Weibull distribution as a reference, rather than the normal distribution, when making predictions.]
Figure 5.29 displays before and after pictures of the effects of a logarithmic transformation on the positively skewed speed variable from the QCI database. Each graph, produced using NCSS, is of the hybrid histogram-density trace-boxplot type first illustrated in Procedure 5.6 . The left graph clearly shows the strong positive skew in the speed scores and the right graph shows the result of taking the log 10 of each raw score.
Combined histogram-density trace-boxplot graphs displaying the before and after effects of a ‘normalising’ log 10 transformation of the speed variable
Notice how the long tail toward slow speed scores is pulled in toward the mean and the very short tail toward fast speed scores is extended away from the mean. The result is a more ‘normal’ appearing distribution. The assumption would then be that we could assume normality of speed scores, but only in a log 10 format (i.e. it is the log of speed scores that we assume is normally distributed in the population). In general, taking the logarithm of raw scores provides a satisfactory remedy for positively skewed distributions (but not for negatively skewed ones). Furthermore, anything we do with the transformed speed scores now has to be interpreted in units of log 10 (seconds) which is a more complex interpretation to make.
Another visual method for detecting non-normality is to graph what is called a normal Q-Q plot (the Q-Q stands for Quantile-Quantile). This plots the percentiles for the observed data against the percentiles for the standard normal distribution (see Cleveland 1995 for more detailed discussion; also see Lane 2007 , http://onlinestatbook.com/2/advanced_graphs/ q-q_plots.html) . If the pattern for the observed data follows a normal distribution, then all the points on the graph will fall approximately along a diagonal line.
Figure 5.30 shows the normal Q-Q plots for the original speed variable and the transformed log-speed variable, produced using the SPSS Explore... procedure. The diagnostic diagonal line is shown on each graph. In the left-hand plot, for speed , the plot points clearly deviate from the diagonal in a way that signals positive skewness. The right-hand plot, for log_speed, shows the plot points generally falling along the diagonal line thereby conforming much more closely to what is expected in a normal distribution.
Normal Q-Q plots for the original speed variable and the new log_speed variable
In addition to visual ways of detecting non-normality, there are also numerical ways. As highlighted in Chap. 1 , there are two additional characteristics of any distribution, namely skewness (asymmetric distribution tails) and kurtosis (peakedness of the distribution). Both have an associated statistic that provides a measure of that characteristic, similar to the mean and standard deviation statistics. In a normal distribution, the values for the skewness and kurtosis statistics are both zero (skewness = 0 means a symmetric distribution; kurtosis = 0 means a mesokurtic distribution). The further away each statistic is from zero, the more the distribution deviates from a normal shape. Both the skewness statistic and the kurtosis statistic have standard errors (see Fundamental Concept VIII ) associated with them (which work very much like the standard deviation, only for a statistic rather than for observations); these can be routinely computed by almost any statistical package when you request a descriptive analysis. Without going into the logic right now (this will come in Fundamental Concept V ), a rough rule of thumb you can use to check for normality using the skewness and kurtosis statistics is to do the following:
Prepare : Take the standard error for the statistic and multiply it by 2 (or 3 if you want to be more conservative).
Interval : Add the result from the Prepare step to the value of the statistic and subtract the result from the value of the statistic. You will end up with two numbers, one low - one high, that define the ends of an interval (what you have just created approximates what is called a ‘confidence interval’, see Procedure 8.3 ).
Check : If zero falls inside of this interval (i.e. between the low and high endpoints from the Interval step), then there is likely to be no significant issue with that characteristic of the distribution. If zero falls outside of the interval (i.e. lower than the low value endpoint or higher than the high value endpoint), then you likely have an issue with non-normality with respect to that characteristic.
Visually, we saw in the left graph in Fig. 5.29 that the speed variable was highly positively skewed. What if Maree wanted to check some numbers to support this judgment? She could ask SPSS to produce the skewness and kurtosis statistics for both the original speed variable and the new log_speed variable using the Frequencies... or the Explore... procedure. Table 5.6 shows what SPSS would produce if the Frequencies ... procedure were used.
Using the 3-step check rule described above, Maree could roughly evaluate the normality of the two variables as follows:
For speed :
skewness : [Prepare] 2 × .229 = .458 ➔ [Interval] 1.487 − .458 = 1.029 and 1.487 + .458 = 1.945 ➔ [Check] zero does not fall inside the interval bounded by 1.029 and 1.945, so there appears to be a significant problem with skewness. Since the value for the skewness statistic (1.487) is positive, this means the problem is positive skewness, confirming what the left graph in Fig. 5.29 showed.
kurtosis : [Prepare] 2 × .455 = .91 ➔ [Interval] 3.071 − .91 = 2.161 and 3.071 + .91 = 3.981 ➔ [Check] zero does not fall in interval bounded by 2.161 and 3.981, so there appears to be a significant problem with kurtosis. Since the value for the kurtosis statistic (1.487) is positive, this means the problem is leptokurtosis—the peakedness of the distribution is too tall relative to what is expected in a normal distribution.
For log_speed:
skewness : [Prepare] 2 × .229 = .458 ➔ [Interval] −.050 − .458 = −.508 and −.050 + .458 = .408 ➔ [Check] zero falls within interval bounded by −.508 and .408, so there appears to be no problem with skewness. The log transform appears to have corrected the problem, confirming what the right graph in Fig. 5.29 showed.
kurtosis : [Prepare] 2 × .455 = .91 ➔ [Interval] −.672 – .91 = −1.582 and −.672 + .91 = .238 ➔ [Check] zero falls within interval bounded by −1.582 and .238, so there appears to be no problem with kurtosis. The log transform appears to have corrected this problem as well, rendering the distribution more approximately mesokurtic (i.e. normal) in shape.
There are also more formal tests of significance (see Fundamental Concept V ) that one can use to numerically evaluate normality, such as the Kolmogorov-Smirnov test and the Shapiro-Wilk’s test . Each of these tests, for example, can be produced by SPSS on request, via the Explore... procedure.
For more information, see Chap. 1 – The language of statistics .
References for Procedure 5.1
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne, VIC: Cengage Learning Australia Pty. ch. 3.
Google Scholar
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. ch. 6 and 8.
Book Google Scholar
Useful Additional Readings for Procedure 5.1
Agresti, A. (2018). Statistical methods for the social sciences (5th ed.). Boston: Pearson. ch. 3.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. ch. 4–5.
MATH Google Scholar
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. ch. 28, 32.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River, NJ: Pearson. ch. 3.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont, CA: Wadsworth Cengage. ch. 2.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 3.
References for Procedure 5.2
Chang, W. (2019). R graphics cookbook: Practical recipes for visualizing data (2nd ed.). Sebastopol, CA: O’Reilly Media. ch. 2–5.
Jacoby, W. G. (1997). Statistical graphics for univariate and bivariate data . Thousand Oaks, CA: Sage.
McCandless, D. (2014). Knowledge is beautiful . London: William Collins.
Smithson, M. J. (2000). Statistics with confidence . London: Sage. ch. 3.
Toseland, M., & Toseland, S. (2012). Infographica: The world as you have never seen it before . London: Quercus Books.
Wilkinson, L. (2009). Cognitive science and graphic design. In SYSTAT Software Inc (Ed.), SYSTAT 13: Graphics (pp. 1–21). Chicago, IL: SYSTAT Software Inc.
Useful Additional Readings for Procedure 5.2
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. ch. 29, 33.
Field, A. (2018). Discovering statistics using SPSS for windows (5th ed.). Los Angeles: Sage. ch. 5.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). Boston, MA: Pearson Education. ch. 5.
Hintze, J. L. (2012). NCSS 8 help system: Graphics . Kaysville, UT: Number Cruncher Statistical Systems. ch. 141–143, 155, 161.
StatPoint Technologies, Inc. (2010). STATGRAPHICS Centurion XVI user manual . Warrenton, VA: StatPoint Technologies Inc.. ch. 4.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 4.
SYSTAT Software Inc. (2009). SYSTAT 13: Graphics . Chicago, IL: SYSTAT Software Inc. ch. 2, 5.
References for Procedure 5.3
Cleveland, W. R. (1995). Visualizing data . Summit, NJ: Hobart Press.
Jacoby, W. J. (1998). Statistical graphics for visualizing multivariate data . Thousand Oaks, CA: Sage.
SYSTAT Software Inc. (2009). SYSTAT 13: Graphics . Chicago, IL: SYSTAT Software Inc. ch. 6.
Useful Additional Readings for Procedure 5.3
Hintze, J. L. (2012). NCSS 8 help system: Graphics . Kaysville, UT: Number Cruncher Statistical Systems. ch. 162.
Kirk, A. (2016). Data visualisation: A handbook for data driven design . Los Angeles: Sage.
Knaflic, C. N. (2015). Storytelling with data: A data visualization guide for business professionals . Hoboken, NJ: Wiley.
Tufte, E. (2001). The visual display of quantitative information (2nd ed.). Cheshire, CN: Graphics Press.
Reference for Procedure 5.4
Field, A. (2018). Discovering statistics using SPSS for windows (5th ed.). Los Angeles: Sage. ch. 6.
Useful Additional Readings for Procedure 5.4
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. ch. 9.
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. ch. 30.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. ch. 7.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River, NJ: Pearson. ch. 4.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont, CA: Wadsworth Cengage. ch. 3.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill Inc. ch. 13.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 5.
References for Procedure 5.5
Useful additional readings for procedure 5.5.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. ch. 11.
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. ch 15.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River, NJ: Pearson. ch. 6.
Gravetter, F. J., & Wallnau, L. B. (2012). Statistics for the behavioural sciences (9th ed.). Belmont, CA: Wadsworth Cengage. ch. 5.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 8.
References for Fundamental Concept I
Smithson, M. J. (2000). Statistics with confidence . London: Sage. ch. 4.
Useful Additional Readings for Fundamental Concept I
Agresti, A. (2018). Statistical methods for the social sciences (5th ed.). Boston: Pearson. ch. 4.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River, NJ: Pearson. ch. 9.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont, CA: Wadsworth Cengage. ch. 6.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont, CA: Cengage Wadsworth. ch. 5.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 10.

References for Procedure 5.6
Norušis, M. J. (2012). IBM SPSS statistics 19 guide to data analysis . Upper Saddle River, NJ: Prentice Hall. ch. 7.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. ch. 5, section 5.5.
Hintze, J. L. (2012). NCSS 8 help system: Introduction . Kaysville, UT: Number Cruncher Statistical System. ch. 152, 200.
StatPoint Technologies, Inc. (2010). STATGRAPHICS Centurion XVI user manual . Warrenton, VA: StatPoint Technologies Inc..
SYSTAT Software Inc. (2009a). SYSTAT 13: Graphics . Chicago, IL: SYSTAT Software Inc. ch. 3.
SYSTAT Software Inc. (2009b). SYSTAT 13: Statistics - I . Chicago, IL: SYSTAT Software Inc. ch. 1 and 9.
Useful Additional Readings for Procedure 5.6
Hartwig, F., & Dearing, B. E. (1979). Exploratory data analysis . Beverly Hills, CA: Sage.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont, CA: Cengage Wadsworth. ch. 2.
Leinhardt, G., & Leinhardt, L. (1997). Exploratory data analysis. In J. P. Keeves (Ed.), Educational research, methodology, and measurement: An international handbook (2nd ed., pp. 519–528). Oxford: Pergamon Press.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill, Inc.. ch. 13.
Tukey, J. W. (1977). Exploratory data analysis . Reading, MA: Addison-Wesley Publishing. [This is the classic text in the area, written by the statistician who developed most of the standard EDA techniques in use today].
Velleman, P. F., & Hoaglin, D. C. (1981). ABC’s of EDA . Boston: Duxbury Press.
Useful Additional Readings for Procedure 5.7
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. ch. 10.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River, NJ: Pearson. ch. 5.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont, CA: Wadsworth Cengage. ch. 4.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 6.
References for Fundemental Concept II
Diebold, F. X., Schuermann, T., & Stroughair, D. (2000). Pitfalls and opportunities in the use of extreme value theory in risk management. The Journal of Risk Finance, 1 (2), 30–35.
Article Google Scholar
Lane, D. (2007). Online statistics education: A multimedia course of study . Houston, TX: Rice University. http://onlinestatbook.com/ .
Useful Additional Readings for Fundemental Concept II
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. ch. 11.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont, CA: Cengage Wadsworth. ch. 3.
Keller, D. K. (2006). The tao of statistics: A path to understanding (with no math) . Thousand Oaks, CA: Sage. ch. 10.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. ch. 7, 8, 9.
Download references
Author information
Authors and affiliations.
UNE Business School, University of New England, Armidale, NSW, Australia
Ray W. Cooksey
You can also search for this author in PubMed Google Scholar
Rights and permissions
Reprints and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this chapter
Cooksey, R.W. (2020). Descriptive Statistics for Summarising Data. In: Illustrating Statistical Procedures: Finding Meaning in Quantitative Data . Springer, Singapore. https://doi.org/10.1007/978-981-15-2537-7_5
Download citation
DOI : https://doi.org/10.1007/978-981-15-2537-7_5
Published : 15 May 2020
Publisher Name : Springer, Singapore
Print ISBN : 978-981-15-2536-0
Online ISBN : 978-981-15-2537-7
eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
- Privacy Policy

Home » Descriptive Statistics – Types, Methods and Examples
Descriptive Statistics – Types, Methods and Examples
Table of Contents

Descriptive Statistics
Descriptive statistics is a branch of statistics that deals with the summarization and description of collected data. This type of statistics is used to simplify and present data in a manner that is easy to understand, often through visual or numerical methods. Descriptive statistics is primarily concerned with measures of central tendency, variability, and distribution, as well as graphical representations of data.
Here are the main components of descriptive statistics:
- Measures of Central Tendency : These provide a summary statistic that represents the center point or typical value of a dataset. The most common measures of central tendency are the mean (average), median (middle value), and mode (most frequent value).
- Measures of Dispersion or Variability : These provide a summary statistic that represents the spread of values in a dataset. Common measures of dispersion include the range (difference between the highest and lowest values), variance (average of the squared differences from the mean), standard deviation (square root of the variance), and interquartile range (difference between the upper and lower quartiles).
- Measures of Position : These are used to understand the distribution of values within a dataset. They include percentiles and quartiles.
- Graphical Representations : Data can be visually represented using various methods like bar graphs, histograms, pie charts, box plots, and scatter plots. These visuals provide a clear, intuitive way to understand the data.
- Measures of Association : These measures provide insight into the relationships between variables in the dataset, such as correlation and covariance.
Descriptive Statistics Types
Descriptive statistics can be classified into two types:
Measures of Central Tendency
These measures help describe the center point or average of a data set. There are three main types:
- Mean : The average value of the dataset, obtained by adding all the data points and dividing by the number of data points.
- Median : The middle value of the dataset, obtained by ordering all data points and picking out the one in the middle (or the average of the two middle numbers if the dataset has an even number of observations).
- Mode : The most frequently occurring value in the dataset.
Measures of Variability (or Dispersion)
These measures describe the spread or variability of the data points in the dataset. There are four main types:
- Range : The difference between the largest and smallest values in the dataset.
- Variance : The average of the squared differences from the mean.
- Standard Deviation : The square root of the variance, giving a measure of dispersion that is in the same units as the original dataset.
- Interquartile Range (IQR) : The range between the first quartile (25th percentile) and the third quartile (75th percentile), which provides a measure of variability that is resistant to outliers.
Descriptive Statistics Formulas
Sure, here are some of the most commonly used formulas in descriptive statistics:
Mean (μ or x̄) :
The average of all the numbers in the dataset. It is computed by summing all the observations and dividing by the number of observations.
Formula : μ = Σx/n or x̄ = Σx/n (where Σx is the sum of all observations and n is the number of observations)
The middle value in the dataset when the observations are arranged in ascending or descending order. If there is an even number of observations, the median is the average of the two middle numbers.
The most frequently occurring number in the dataset. There’s no formula for this as it’s determined by observation.
The difference between the highest (max) and lowest (min) values in the dataset.
Formula : Range = max – min
Variance (σ² or s²) :
The average of the squared differences from the mean. Variance is a measure of how spread out the numbers in the dataset are.
Population Variance formula : σ² = Σ(x – μ)² / N Sample Variance formula: s² = Σ(x – x̄)² / (n – 1)
(where x is each individual observation, μ is the population mean, x̄ is the sample mean, N is the size of the population, and n is the size of the sample)
Standard Deviation (σ or s) :
The square root of the variance. It measures the amount of variability or dispersion for a set of data. Population Standard Deviation formula: σ = √σ² Sample Standard Deviation formula: s = √s²
Interquartile Range (IQR) :
The range between the first quartile (Q1, 25th percentile) and the third quartile (Q3, 75th percentile). It measures statistical dispersion, or how far apart the data points are.
Formula : IQR = Q3 – Q1
Descriptive Statistics Methods
Here are some of the key methods used in descriptive statistics:
This method involves arranging data into a table format, making it easier to understand and interpret. Tables often show the frequency distribution of variables.
Graphical Representation
This method involves presenting data visually to help reveal patterns, trends, outliers, or relationships between variables. There are many types of graphs used, such as bar graphs, histograms, pie charts, line graphs, box plots, and scatter plots.
Calculation of Central Tendency Measures
This involves determining the mean, median, and mode of a dataset. These measures indicate where the center of the dataset lies.
Calculation of Dispersion Measures
This involves calculating the range, variance, standard deviation, and interquartile range. These measures indicate how spread out the data is.
Calculation of Position Measures
This involves determining percentiles and quartiles, which tell us about the position of particular data points within the overall data distribution.
Calculation of Association Measures
This involves calculating statistics like correlation and covariance to understand relationships between variables.
Summary Statistics
Often, a collection of several descriptive statistics is presented together in what’s known as a “summary statistics” table. This provides a comprehensive snapshot of the data at a glanc
Descriptive Statistics Examples
Descriptive Statistics Examples are as follows:
Example 1: Student Grades
Let’s say a teacher has the following set of grades for 7 students: 85, 90, 88, 92, 78, 88, and 94. The teacher could use descriptive statistics to summarize this data:
- Mean (average) : (85 + 90 + 88 + 92 + 78 + 88 + 94)/7 = 88
- Median (middle value) : First, rearrange the grades in ascending order (78, 85, 88, 88, 90, 92, 94). The median grade is 88.
- Mode (most frequent value) : The grade 88 appears twice, more frequently than any other grade, so it’s the mode.
- Range (difference between highest and lowest) : 94 (highest) – 78 (lowest) = 16
- Variance and Standard Deviation : These would be calculated using the appropriate formulas, providing a measure of the dispersion of the grades.
Example 2: Survey Data
A researcher conducts a survey on the number of hours of TV watched per day by people in a particular city. They collect data from 1,000 respondents and can use descriptive statistics to summarize this data:
- Mean : Calculate the average hours of TV watched by adding all the responses and dividing by the total number of respondents.
- Median : Sort the data and find the middle value.
- Mode : Identify the most frequently reported number of hours watched.
- Histogram : Create a histogram to visually display the frequency of responses. This could show, for example, that the majority of people watch 2-3 hours of TV per day.
- Standard Deviation : Calculate this to find out how much variation there is from the average.
Importance of Descriptive Statistics
Descriptive statistics are fundamental in the field of data analysis and interpretation, as they provide the first step in understanding a dataset. Here are a few reasons why descriptive statistics are important:
- Data Summarization : Descriptive statistics provide simple summaries about the measures and samples you have collected. With a large dataset, it’s often difficult to identify patterns or tendencies just by looking at the raw data. Descriptive statistics provide numerical and graphical summaries that can highlight important aspects of the data.
- Data Simplification : They simplify large amounts of data in a sensible way. Each descriptive statistic reduces lots of data into a simpler summary, making it easier to understand and interpret the dataset.
- Identification of Patterns and Trends : Descriptive statistics can help identify patterns and trends in the data, providing valuable insights. Measures like the mean and median can tell you about the central tendency of your data, while measures like the range and standard deviation tell you about the dispersion.
- Data Comparison : By summarizing data into measures such as the mean and standard deviation, it’s easier to compare different datasets or different groups within a dataset.
- Data Quality Assessment : Descriptive statistics can help identify errors or outliers in the data, which might indicate issues with data collection or entry.
- Foundation for Further Analysis : Descriptive statistics are typically the first step in data analysis. They help create a foundation for further statistical or inferential analysis. In fact, advanced statistical techniques often assume that one has first examined their data using descriptive methods.
When to use Descriptive Statistics
They can be used in a wide range of situations, including:
- Understanding a New Dataset : When you first encounter a new dataset, using descriptive statistics is a useful first step to understand the main characteristics of the data, such as the central tendency, dispersion, and distribution.
- Data Exploration in Research : In the initial stages of a research project, descriptive statistics can help to explore the data, identify trends and patterns, and generate hypotheses for further testing.
- Presenting Research Findings : Descriptive statistics can be used to present research findings in a clear and understandable way, often using visual aids like graphs or charts.
- Monitoring and Quality Control : In fields like business or manufacturing, descriptive statistics are often used to monitor processes, track performance over time, and identify any deviations from expected standards.
- Comparing Groups : Descriptive statistics can be used to compare different groups or categories within your data. For example, you might want to compare the average scores of two groups of students, or the variance in sales between different regions.
- Reporting Survey Results : If you conduct a survey, you would use descriptive statistics to summarize the responses, such as calculating the percentage of respondents who agree with a certain statement.
Applications of Descriptive Statistics
Descriptive statistics are widely used in a variety of fields to summarize, represent, and analyze data. Here are some applications:
- Business : Businesses use descriptive statistics to summarize and interpret data such as sales figures, customer feedback, or employee performance. For instance, they might calculate the mean sales for each month to understand trends, or use graphical representations like bar charts to present sales data.
- Healthcare : In healthcare, descriptive statistics are used to summarize patient data, such as age, weight, blood pressure, or cholesterol levels. They are also used to describe the incidence and prevalence of diseases in a population.
- Education : Educators use descriptive statistics to summarize student performance, like average test scores or grade distribution. This information can help identify areas where students are struggling and inform instructional decisions.
- Social Sciences : Social scientists use descriptive statistics to summarize data collected from surveys, experiments, and observational studies. This can involve describing demographic characteristics of participants, response frequencies to survey items, and more.
- Psychology : Psychologists use descriptive statistics to describe the characteristics of their study participants and the main findings of their research, such as the average score on a psychological test.
- Sports : Sports analysts use descriptive statistics to summarize athlete and team performance, such as batting averages in baseball or points per game in basketball.
- Government : Government agencies use descriptive statistics to summarize data about the population, such as census data on population size and demographics.
- Finance and Economics : In finance, descriptive statistics can be used to summarize past investment performance or economic data, such as changes in stock prices or GDP growth rates.
- Quality Control : In manufacturing, descriptive statistics can be used to summarize measures of product quality, such as the average dimensions of a product or the frequency of defects.
Limitations of Descriptive Statistics
While descriptive statistics are a crucial part of data analysis and provide valuable insights about a dataset, they do have certain limitations:
- Lack of Depth : Descriptive statistics provide a summary of your data, but they can oversimplify the data, resulting in a loss of detail and potentially significant nuances.
- Vulnerability to Outliers : Some descriptive measures, like the mean, are sensitive to outliers. A single extreme value can significantly skew your mean, making it less representative of your data.
- Inability to Make Predictions : Descriptive statistics describe what has been observed in a dataset. They don’t allow you to make predictions or generalizations about unobserved data or larger populations.
- No Insight into Correlations : While some descriptive statistics can hint at potential relationships between variables, they don’t provide detailed insights into the nature or strength of these relationships.
- No Causality or Hypothesis Testing : Descriptive statistics cannot be used to determine cause and effect relationships or to test hypotheses. For these purposes, inferential statistics are needed.
- Can Mislead : When used improperly, descriptive statistics can be used to present a misleading picture of the data. For instance, choosing to only report the mean without also reporting the standard deviation or range can hide a large amount of variability in the data.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Discourse Analysis – Methods, Types and Examples

Multidimensional Scaling – Types, Formulas and...

Histogram – Types, Examples and Making Guide

Factor Analysis – Steps, Methods and Examples

Content Analysis – Methods, Types and Examples

Critical Analysis – Types, Examples and Writing...
Purdue Online Writing Lab Purdue OWL® College of Liberal Arts
Descriptive Statistics

Welcome to the Purdue OWL
This page is brought to you by the OWL at Purdue University. When printing this page, you must include the entire legal notice.
Copyright ©1995-2018 by The Writing Lab & The OWL at Purdue and Purdue University. All rights reserved. This material may not be published, reproduced, broadcast, rewritten, or redistributed without permission. Use of this site constitutes acceptance of our terms and conditions of fair use.
The mean, the mode, the median, the range, and the standard deviation are all examples of descriptive statistics. Descriptive statistics are used because in most cases, it isn't possible to present all of your data in any form that your reader will be able to quickly interpret.
Generally, when writing descriptive statistics, you want to present at least one form of central tendency (or average), that is, either the mean, median, or mode. In addition, you should present one form of variability , usually the standard deviation.
Measures of Central Tendency and Other Commonly Used Descriptive Statistics
The mean, median, and the mode are all measures of central tendency. They attempt to describe what the typical data point might look like. In essence, they are all different forms of 'the average.' When writing statistics, you never want to say 'average' because it is difficult, if not impossible, for your reader to understand if you are referring to the mean, the median, or the mode.
The mean is the most common form of central tendency, and is what most people usually are referring to when the say average. It is simply the total sum of all the numbers in a data set, divided by the total number of data points. For example, the following data set has a mean of 4: {-1, 0, 1, 16}. That is, 16 divided by 4 is 4. If there isn't a good reason to use one of the other forms of central tendency, then you should use the mean to describe the central tendency.
The median is simply the middle value of a data set. In order to calculate the median, all values in the data set need to be ordered, from either highest to lowest, or vice versa. If there are an odd number of values in a data set, then the median is easy to calculate. If there is an even number of values in a data set, then the calculation becomes more difficult. Statisticians still debate how to properly calculate a median when there is an even number of values, but for most purposes, it is appropriate to simply take the mean of the two middle values. The median is useful when describing data sets that are skewed or have extreme values. Incomes of baseballs players, for example, are commonly reported using a median because a small minority of baseball players makes a lot of money, while most players make more modest amounts. The median is less influenced by extreme scores than the mean.
The mode is the most commonly occurring number in the data set. The mode is best used when you want to indicate the most common response or item in a data set. For example, if you wanted to predict the score of the next football game, you may want to know what the most common score is for the visiting team, but having an average score of 15.3 won't help you if it is impossible to score 15.3 points. Likewise, a median score may not be very informative either, if you are interested in what score is most likely.
Standard Deviation
The standard deviation is a measure of variability (it is not a measure of central tendency). Conceptually it is best viewed as the 'average distance that individual data points are from the mean.' Data sets that are highly clustered around the mean have lower standard deviations than data sets that are spread out.
For example, the first data set would have a higher standard deviation than the second data set:
Notice that both groups have the same mean (5) and median (also 5), but the two groups contain different numbers and are organized much differently. This organization of a data set is often referred to as a distribution. Because the two data sets above have the same mean and median, but different standard deviation, we know that they also have different distributions. Understanding the distribution of a data set helps us understand how the data behave.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Ann Card Anaesth
- v.22(1); Jan-Mar 2019
Descriptive Statistics and Normality Tests for Statistical Data
Prabhaker mishra.
Department of Biostatistics and Health Informatics, Sanjay Gandhi Postgraduate Institute of Medical Sciences, Lucknow, Uttar Pradesh, India
Chandra M Pandey
Uttam singh, anshul gupta.
1 Department of Haematology, Sanjay Gandhi Postgraduate Institute of Medical Sciences, Lucknow, Uttar Pradesh, India
Chinmoy Sahu
2 Department of Microbiology, Sanjay Gandhi Postgraduate Institute of Medical Sciences, Lucknow, Uttar Pradesh, India
Amit Keshri
3 Department of Neuro-Otology, Sanjay Gandhi Postgraduate Institute of Medical Sciences, Lucknow, Uttar Pradesh, India
Descriptive statistics are an important part of biomedical research which is used to describe the basic features of the data in the study. They provide simple summaries about the sample and the measures. Measures of the central tendency and dispersion are used to describe the quantitative data. For the continuous data, test of the normality is an important step for deciding the measures of central tendency and statistical methods for data analysis. When our data follow normal distribution, parametric tests otherwise nonparametric methods are used to compare the groups. There are different methods used to test the normality of data, including numerical and visual methods, and each method has its own advantages and disadvantages. In the present study, we have discussed the summary measures and methods used to test the normality of the data.
Introduction
A data set is a collection of the data of individual cases or subjects. Usually, it is meaningless to present such data individually because that will not produce any important conclusions. In place of individual case presentation, we present summary statistics of our data set with or without analytical form which can be easily absorbable for the audience. Statistics which is a science of collection, analysis, presentation, and interpretation of the data, have two main branches, are descriptive statistics and inferential statistics.[ 1 ]
Summary measures or summary statistics or descriptive statistics are used to summarize a set of observations, in order to communicate the largest amount of information as simply as possible. Descriptive statistics are the kind of information presented in just a few words to describe the basic features of the data in a study such as the mean and standard deviation (SD).[ 2 , 3 ] The another is inferential statistics, which draw conclusions from data that are subject to random variation (e.g., observational errors and sampling variation). In inferential statistics, most predictions are for the future and generalizations about a population by studying a smaller sample.[ 2 , 4 ] To draw the inference from the study participants in terms of different groups, etc., statistical methods are used. These statistical methods have some assumptions including normality of the continuous data. There are different methods used to test the normality of data, including numerical and visual methods, and each method has its own advantages and disadvantages.[ 5 ] Descriptive statistics and inferential statistics both are employed in scientific analysis of data and are equally important in the statistics. In the present study, we have discussed the summary measures to describe the data and methods used to test the normality of the data. To understand the descriptive statistics and test of the normality of the data, an example [ Table 1 ] with a data set of 15 patients whose mean arterial pressure (MAP) was measured are given below. Further examples related to the measures of central tendency, dispersion, and tests of normality are discussed based on the above data.
Distribution of mean arterial pressure (mmHg) as per sex
| Patient number | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| MAP | 82 | 84 | 85 | 88 | 92 | 93 | 94 | 95 | 98 | 100 | 102 | 107 | 110 | 116 | 116 | |
| Sex | M | F | F | M | M | F | F | M | M | F | M | F | M | F | M | |
MAP: Mean arterial pressure, M: Male, F: Female
Descriptive Statistics
There are three major types of descriptive statistics: Measures of frequency (frequency, percent), measures of central tendency (mean, median and mode), and measures of dispersion or variation (variance, SD, standard error, quartile, interquartile range, percentile, range, and coefficient of variation [CV]) provide simple summaries about the sample and the measures. A measure of frequency is usually used for the categorical data while others are used for quantitative data.
Measures of Frequency
Frequency statistics simply count the number of times that in each variable occurs, such as the number of males and females within the sample or population. Frequency analysis is an important area of statistics that deals with the number of occurrences (frequency) and percentage. For example, according to Table 1 , out of the 15 patients, frequency of the males and females were 8 (53.3%) and 7 (46.7%), respectively.
Measures of Central Tendency
Data are commonly describe the observations in a measure of central tendency, which is also called measures of central location, is used to find out the representative value of a data set. The mean, median, and mode are three types of measures of central tendency. Measures of central tendency give us one value (mean or median) for the distribution and this value represents the entire distribution. To make comparisons between two or more groups, representative values of these distributions are compared. It helps in further statistical analysis because many techniques of statistical analysis such as measures of dispersion, skewness, correlation, t -test, and ANOVA test are calculated using value of measures of central tendency. That is why measures of central tendency are also called as measures of the first order. A representative value (measures of central tendency) is considered good when it was calculated using all observations and not affected by extreme values because these values are used to calculate for further measures.
Computation of Measures of Central Tendency
Mean is the mathematical average value of a set of data. Mean can be calculated using summation of the observations divided by number of observations. It is the most popular measure and very easy to calculate. It is a unique value for one group, that is, there is only one answer, which is useful when comparing between the groups. In the computation of mean, all the observations are used.[ 2 , 5 ] One disadvantage with mean is that it is affected by extreme values (outliers). For example, according to Table 2 , mean MAP of the patients was 97.47 indicated that average MAP of the patients was 97.47 mmHg.
Descriptive statistics of the mean arterial pressure (mmHg)
| Mean | SD | SE | Q1 | Q2 | Q3 | Minimum | Maximum | Mode |
|---|---|---|---|---|---|---|---|---|
| 97.47 | 11.01 | 2.84 | 88 | 95 | 107 | 82 | 116 | 116 |
SD: Standard deviation, SE: Standard error, Q1: First quartile, Q2: Second quartile, Q3: Third quartile
The median is defined as the middle most observation if data are arranged either in increasing or decreasing order of magnitude. Thus, it is one of the observations, which occupies the central place in the distribution (data). This is also called positional average. Extreme values (outliers) do not affect the median. It is unique, that is, there is only one median of one data set which is useful when comparing between the groups. There is one disadvantage of median over mean that it is not as popular as mean.[ 6 ] For example, according to Table 2 , median MAP of the patients was 95 mmHg indicated that 50% observations of the data are either less than or equal to the 95 mmHg and rest of the 50% observations are either equal or greater than 95 mmHg.
Mode is a value that occurs most frequently in a set of observation, that is, the observation, which has maximum frequency is called mode. In a data set, it is possible to have multiple modes or no mode exists. Due to the possibility of the multiple modes for one data set, it is not used to compare between the groups. For example, according to Table 2 , maximum repeated value is 116 mmHg (2 times) rest are repeated one time only, mode of the data is 116 mmHg.
Measures of Dispersion
Measures of dispersion is another measure used to show how spread out (variation) in a data set also called measures of variation. It is quantitatively degree of variation or dispersion of values in a population or in a sample. More specifically, it is showing lack of representation of measures of central tendency usually for mean/median. These are indices that give us an idea about homogeneity or heterogeneity of the data.[ 2 , 6 ]
Common measures
Variance, SD, standard error, quartile, interquartile range, percentile, range, and CV.
Computation of Measures of Dispersion
Standard deviation and variance.
The SD is a measure of how spread out values is from its mean value. Its symbol is σ (the Greek letter sigma) or s. It is called SD because we have taken a standard value (mean) to measures the dispersion. Where x i is individual value, x ̄ is mean value. If sample size is <30, we use “ n -1” in denominator, for sample size ≥30, use “ n ” in denominator. The variance (s 2 ) is defined as the average of the squared difference from the mean. It is equal to the square of the SD (s).

For example, in the above, SD is 11.01 mmHg When n <30 which showed that approximate average deviation between mean value and individual values is 11.01. Similarly, variance is 121.22 [i.e., (11.01) 2 ], which showed that average square deviation between mean value and individual values is 121.22 [ Table 2 ].
Standard error
Standard error is the approximate difference between sample mean and population mean. When we draw the many samples from same population with same sample size through random sampling technique, then SD among the sample means is called standard error. If sample SD and sample size are given, we can calculate standard error for this sample, by using the formula.
Standard error = sample SD/√sample size.
For example, according to Table 2 , standard error is 2.84 mmHg, which showed that average mean difference between sample means and population mean is 2.84 mmHg [ Table 2 ].
Quartiles and interquartile range
The quartiles are the three points that divide the data set into four equal groups, each group comprising a quarter of the data, for a set of data values which are arranged in either ascending or descending order. Q1, Q2, and Q3 are represent the first, second, and third quartile's value.[ 7 ]
For ith Quartile = [i * (n + 1)/4] th observation, where i = 1, 2, 3.
For example, in the above, first quartile (Q1) = (n + 1)/4= (15 + 1)/4 = 4 th observation from initial = 88 mmHg (i.e., first 25% number of observations of the data are either ≤88 and rest 75% observations are either ≥88), Q2 (also called median) = [2* (n + 1)/4] = 8 th observation from initial = 95 mmHg, that is, first 50% number of observations of the data are either less or equal to the 95 and rest 50% observations are either ≥95, and similarly Q3 = [3* (n + 1)/4] = 12 th observation from initial = 107 mmHg, i.e., indicated that first 75% number of observations of the data are either ≤107 and rest 25% observations are either ≥107. The interquartile range (IQR) is a measure of variability, also called the midspread or middle 50%, which is a measure of statistical dispersion, being equal to the difference between 75 th (Q3 or third quartile) and 25 th (Q1 or first quartile) percentiles. For example, in the above example, three quartiles, that is, Q1, Q2, and Q3 are 88, 95, and 107, respectively. As the first and third quartile in the data is 88 and 107. Hence, IQR of the data is 19 mmHg (also can write like: 88–107) [ Table 2 ].

The percentiles are the 99 points that divide the data set into 100 equal groups, each group comprising a 1% of the data, for a set of data values which are arranged in either ascending or descending order. About 25% percentile is the first quartile, 50% percentile is the second quartile also called median value, while 75% percentile is the third quartile of the data.
For ith percentile = [i * (n + 1)/100] th observation, where i = 1, 2, 3.,99.
Example: In the above, 10 th percentile = [10* (n + 1)/100] =1.6 th observation from initial which is fall between the first and second observation from the initial = 1 st observation + 0.6* (difference between the second and first observation) = 83.20 mmHg, which indicated that 10% of the data are either ≤83.20 and rest 90% observations are either ≥83.20.

Coefficient of Variation
Interpretation of SD without considering the magnitude of mean of the sample or population may be misleading. To overcome this problem, CV gives an idea. CV gives the result in terms of ratio of SD with respect to its mean value, which expressed in %. CV = 100 × (SD/mean). For example, in the above, coefficient of the variation is 11.3% which indicated that SD is 11.3% of its mean value [i.e., 100* (11.01/97.47)] [ Table 2 ].
Difference between largest and smallest observation is called range. If A and B are smallest and largest observations in a data set, then the range (R) is equal to the difference of largest and smallest observation, that is, R = A−B.
For example, in the above, minimum and maximum observation in the data is 82 mmHg and 116 mmHg. Hence, the range of the data is 34 mmHg (also can write like: 82–116) [ Table 2 ].
Descriptive statistics can be calculated in the statistical software “SPSS” (analyze → descriptive statistics → frequencies or descriptives.
Normality of data and testing
The standard normal distribution is the most important continuous probability distribution has a bell-shaped density curve described by its mean and SD and extreme values in the data set have no significant impact on the mean value. If a continuous data is follow normal distribution then 68.2%, 95.4%, and 99.7% observations are lie between mean ± 1 SD, mean ± 2 SD, and mean ± 3 SD, respectively.[ 2 , 4 ]
Why to test the normality of data
Various statistical methods used for data analysis make assumptions about normality, including correlation, regression, t -tests, and analysis of variance. Central limit theorem states that when sample size has 100 or more observations, violation of the normality is not a major issue.[ 5 , 8 ] Although for meaningful conclusions, assumption of the normality should be followed irrespective of the sample size. If a continuous data follow normal distribution, then we present this data in mean value. Further, this mean value is used to compare between/among the groups to calculate the significance level ( P value). If our data are not normally distributed, resultant mean is not a representative value of our data. A wrong selection of the representative value of a data set and further calculated significance level using this representative value might give wrong interpretation.[ 9 ] That is why, first we test the normality of the data, then we decide whether mean is applicable as representative value of the data or not. If applicable, then means are compared using parametric test otherwise medians are used to compare the groups, using nonparametric methods.
Methods used for test of normality of data
An assessment of the normality of data is a prerequisite for many statistical tests because normal data is an underlying assumption in parametric testing. There are two main methods of assessing normality: Graphical and numerical (including statistical tests).[ 3 , 4 ] Statistical tests have the advantage of making an objective judgment of normality but have the disadvantage of sometimes not being sensitive enough at low sample sizes or overly sensitive to large sample sizes. Graphical interpretation has the advantage of allowing good judgment to assess normality in situations when numerical tests might be over or undersensitive. Although normality assessment using graphical methods need a great deal of the experience to avoid the wrong interpretations. If we do not have a good experience, it is the best to rely on the numerical methods.[ 10 ] There are various methods available to test the normality of the continuous data, out of them, most popular methods are Shapiro–Wilk test, Kolmogorov–Smirnov test, skewness, kurtosis, histogram, box plot, P–P Plot, Q–Q Plot, and mean with SD. The two well-known tests of normality, namely, the Kolmogorov–Smirnov test and the Shapiro–Wilk test are most widely used methods to test the normality of the data. Normality tests can be conducted in the statistical software “SPSS” (analyze → descriptive statistics → explore → plots → normality plots with tests).
The Shapiro–Wilk test is more appropriate method for small sample sizes (<50 samples) although it can also be handling on larger sample size while Kolmogorov–Smirnov test is used for n ≥50. For both of the above tests, null hypothesis states that data are taken from normal distributed population. When P > 0.05, null hypothesis accepted and data are called as normally distributed. Skewness is a measure of symmetry, or more precisely, the lack of symmetry of the normal distribution. Kurtosis is a measure of the peakedness of a distribution. The original kurtosis value is sometimes called kurtosis (proper). Most of the statistical packages such as SPSS provide “excess” kurtosis (also called kurtosis [excess]) obtained by subtracting 3 from the kurtosis (proper). A distribution, or data set, is symmetric if it looks the same to the left and right of the center point. If mean, median, and mode of a distribution coincide, then it is called a symmetric distribution, that is, skewness = 0, kurtosis (excess) = 0. A distribution is called approximate normal if skewness or kurtosis (excess) of the data are between − 1 and + 1. Although this is a less reliable method in the small-to-moderate sample size (i.e., n <300) because it can not adjust the standard error (as the sample size increases, the standard error decreases). To overcome this problem, a z -test is applied for normality test using skewness and kurtosis. A Z score could be obtained by dividing the skewness values or excess kurtosis value by their standard errors. For small sample size ( n <50), z value ± 1.96 are sufficient to establish normality of the data.[ 8 ] However, medium-sized samples (50≤ n <300), at absolute z -value ± 3.29, conclude the distribution of the sample is normal.[ 11 ] For sample size >300, normality of the data is depend on the histograms and the absolute values of skewness and kurtosis. Either an absolute skewness value ≤2 or an absolute kurtosis (excess) ≤4 may be used as reference values for determining considerable normality.[ 11 ] A histogram is an estimate of the probability distribution of a continuous variable. If the graph is approximately bell-shaped and symmetric about the mean, we can assume normally distributed data[ 12 , 13 ] [ Figure 1 ]. In statistics, a Q–Q plot is a scatterplot created by plotting two sets of quantiles (observed and expected) against one another. For normally distributed data, observed data are approximate to the expected data, that is, they are statistically equal [ Figure 2 ]. A P–P plot (probability–probability plot or percent–percent plot) is a graphical technique for assessing how closely two data sets (observed and expected) agree. It forms an approximate straight line when data are normally distributed. Departures from this straight line indicate departures from normality [ Figure 3 ]. Box plot is another way to assess the normality of the data. It shows the median as a horizontal line inside the box and the IQR (range between the first and third quartile) as the length of the box. The whiskers (line extending from the top and bottom of the box) represent the minimum and maximum values when they are within 1.5 times the IQR from either end of the box (i.e., Q1 − 1.5* IQR and Q3 + 1.5* IQR). Scores >1.5 times and 3 times the IQR are out of the box plot and are considered as outliers and extreme outliers, respectively. A box plot that is symmetric with the median line at approximately the center of the box and with symmetric whiskers indicate that the data may have come from a normal distribution. In case many outliers are present in our data set, either outliers are need to remove or data should treat as nonnormally distributed[ 8 , 13 , 14 ] [ Figure 4 ]. Another method of normality of the data is relative value of the SD with respect to mean. If SD is less than half mean (i.e., CV <50%), data are considered normal.[ 15 ] This is the quick method to test the normality. However this method should only be used when our sample size is at least 50.

Histogram showing the distribution of the mean arterial pressure

Normal Q–Q Plot showing correlation between observed and expected values of the mean arterial pressure

Normal P–P Plot showing correlation between observed and expected cumulative probability of the mean arterial pressure

Boxplot showing distribution of the mean arterial pressure
For example in Table 1 , data of MAP of the 15 patients are given. Normality of the above data was assessed. Result showed that data were normally distributed as skewness (0.398) and kurtosis (−0.825) individually were within ±1. Critical ratio ( Z value) of the skewness (0.686) and kurtosis (−0.737) were within ±1.96, also evident to normally distributed. Similarly, Shapiro–Wilk test ( P = 0.454) and Kolmogorov–Smirnov test ( P = 0.200) were statistically insignificant, that is, data were considered normally distributed. As sample size is <50, we have to take Shapiro–Wilk test result and Kolmogorov–Smirnov test result must be avoided, although both methods indicated that data were normally distributed. As SD of the MAP was less than half mean value (11.01 <48.73), data were considered normally distributed, although due to sample size <50, we should avoid this method because it should use when our sample size is at least 50 [Tables [Tables2 2 and and3 3 ].
Skewness, kurtosis, and normality tests for mean arterial pressure (mmHg)
| Variable | Skewness | Kurtosis | ||||||
|---|---|---|---|---|---|---|---|---|
| Value | SE | Value | SE | K-S test with Lilliefors correction | Shapiro-Wilk test | |||
| MAP score | 0.398 | 0.580 | 0.686 | −0.825 | 1.12 | −0.737 | 0.200 | 0.454 |
K-S: Kolmogorov–Smirnov, SD: Standard deviation, SE: Standard error
Conclusions
Descriptive statistics are a statistical method to summarizing data in a valid and meaningful way. A good and appropriate measure is important not only for data but also for statistical methods used for hypothesis testing. For continuous data, testing of normality is very important because based on the normality status, measures of central tendency, dispersion, and selection of parametric/nonparametric test are decided. Although there are various methods for normality testing but for small sample size ( n <50), Shapiro–Wilk test should be used as it has more power to detect the nonnormality and this is the most popular and widely used method. When our sample size ( n ) is at least 50, any other methods (Kolmogorov–Smirnov test, skewness, kurtosis, z value of the skewness and kurtosis, histogram, box plot, P–P Plot, Q–Q Plot, and SD with respect to mean) can be used to test of the normality of continuous data.
Financial support and sponsorship
Conflicts of interest.
There are no conflicts of interest.
Acknowledgment
The authors would like to express their deep and sincere gratitude to Dr. Prabhat Tiwari, Professor, Department of Anaesthesiology, Sanjay Gandhi Postgraduate Institute of Medical Sciences, Lucknow, for his critical comments and useful suggestions that was very much useful to improve the quality of this manuscript.
Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service
Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve
Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground
Know how your people feel and empower managers to improve employee engagement, productivity, and retention
Take action in the moments that matter most along the employee journey and drive bottom line growth
Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people
Get faster, richer insights with qual and quant tools that make powerful market research available to everyone
Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts
Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market
Explore the platform powering Experience Management
- Free Account
- Product Demos
- For Digital
- For Customer Care
- For Human Resources
- For Researchers
- Financial Services
- All Industries
Popular Use Cases
- Customer Experience
- Employee Experience
- Net Promoter Score
- Voice of Customer
- Customer Success Hub
- Product Documentation
- Training & Certification
- XM Institute
- Popular Resources
- Customer Stories
- Artificial Intelligence
Market Research
- Partnerships
- Marketplace
The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.
- English/AU & NZ
- Español/Europa
- Español/América Latina
- Português Brasileiro
- REQUEST DEMO
- Experience Management
- Descriptive Statistics
Try Qualtrics for free
Descriptive statistics in research: a critical component of data analysis.
15 min read With any data, the object is to describe the population at large, but what does that mean and what processes, methods and measures are used to uncover insights from that data? In this short guide, we explore descriptive statistics and how it’s applied to research.
What do we mean by descriptive statistics?
With any kind of data, the main objective is to describe a population at large — and using descriptive statistics, researchers can quantify and describe the basic characteristics of a given data set.
For example, researchers can condense large data sets, which may contain thousands of individual data points or observations, into a series of statistics that provide useful information on the population of interest. We call this process “describing data”.
In the process of producing summaries of the sample, we use measures like mean, median, variance, graphs, charts, frequencies, histograms, box and whisker plots, and percentages. For datasets with just one variable, we use univariate descriptive statistics. For datasets with multiple variables, we use bivariate correlation and multivariate descriptive statistics.
Want to find out the definitions?
Univariate descriptive statistics: this is when you want to describe data with only one characteristic or attribute
Bivariate correlation: this is when you simultaneously analyze (compare) two variables to see if there is a relationship between them
Multivariate descriptive statistics: this is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable
Then, after describing and summarizing the data, as well as using simple graphical analyses, we can start to draw meaningful insights from it to help guide specific strategies. It’s also important to note that descriptive statistics can employ and use both quantitative and qualitative research .
Describing data is undoubtedly the most critical first step in research as it enables the subsequent organization, simplification and summarization of information — and every survey question and population has summary statistics. Let’s take a look at a few examples.
Examples of descriptive statistics
Consider for a moment a number used to summarize how well a striker is performing in football — goals scored per game. This number is simply the number of shots taken against how many of those shots hit the back of the net (reported to three significant digits). If a striker is scoring 0.333, that’s one goal for every three shots. If they’re scoring one in four, that’s 0.250.
A classic example is a student’s grade point average (GPA). This single number describes the general performance of a student across a range of course experiences and classes. It doesn’t tell us anything about the difficulty of the courses the student is taking, or what those courses are, but it does provide a summary that enables a degree of comparison with people or other units of data.
Ultimately, descriptive statistics make it incredibly easy for people to understand complex (or data intensive) quantitative or qualitative insights across large data sets.
Take your research to the next level with XM for Strategy & Research
Types of descriptive statistics
To quantitatively summarize the characteristics of raw, ungrouped data, we use the following types of descriptive statistics:
- Measures of Central Tendency ,
- Measures of Dispersion and
- Measures of Frequency Distribution.
Following the application of any of these approaches, the raw data then becomes ‘grouped’ data that’s logically organized and easy to understand. To visually represent the data, we then use graphs, charts, tables etc.
Let’s look at the different types of measurement and the statistical methods that belong to each:
Measures of Central Tendency are used to describe data by determining a single representative of central value. For example, the mean, median or mode.
Measures of Dispersion are used to determine how spread out a data distribution is with respect to the central value, e.g. the mean, median or mode. For example, while central tendency gives the person the average or central value, it doesn’t describe how the data is distributed within the set.
Measures of Frequency Distribution are used to describe the occurrence of data within the data set (count).
The methods of each measure are summarized in the table below:
| Measures of Central Tendency | Measures of Dispersion | Measures of Frequency Distribution |
|---|---|---|
| Mean | Range | Count |
| Median | Standard deviation | |
| Mode | Quartile deviation | |
| Variance | ||
| Absolute deviation |
Mean: The most popular and well-known measure of central tendency. The mean is equal to the sum of all the values in the data set divided by the number of values in the data set.
Median: The median is the middle score for a set of data that has been arranged in order of magnitude. If you have an even number of data, e.g. 10 data points, take the two middle scores and average the result.
Mode: The mode is the most frequently occurring observation in the data set.
Range: The difference between the highest and lowest value.
Standard deviation: Standard deviation measures the dispersion of a data set relative to its mean and is calculated as the square root of the variance.
Quartile deviation : Quartile deviation measures the deviation in the middle of the data.
Variance: Variance measures the variability from the average of mean.
Absolute deviation: The absolute deviation of a dataset is the average distance between each data point and the mean.
Count: How often each value occurs.
Scope of descriptive statistics in research
Descriptive statistics (or analysis) is considered more vast than other quantitative and qualitative methods as it provides a much broader picture of an event, phenomenon or population.
But that’s not all: it can use any number of variables, and as it collects data and describes it as it is, it’s also far more representative of the world as it exists.
However, it’s also important to consider that descriptive analyses lay the foundation for further methods of study. By summarizing and condensing the data into easily understandable segments, researchers can further analyze the data to uncover new variables or hypotheses.
Mostly, this practice is all about the ease of data visualization. With data presented in a meaningful way, researchers have a simplified interpretation of the data set in question. That said, while descriptive statistics helps to summarize information, it only provides a general view of the variables in question.
It is, therefore, up to the researchers to probe further and use other methods of analysis to discover deeper insights.
Things you can do with descriptive statistics
Define subject characteristics
If a marketing team wanted to build out accurate buyer personas for specific products and industry verticals, they could use descriptive analyses on customer datasets (procured via a survey) to identify consistent traits and behaviors.
They could then ‘describe’ the data to build a clear picture and understanding of who their buyers are, including things like preferences, business challenges, income and so on.
Measure data trends
Let’s say you wanted to assess propensity to buy over several months or years for a specific target market and product. With descriptive statistics, you could quickly summarize the data and extract the precise data points you need to understand the trends in product purchase behavior.
Compare events, populations or phenomena
How do different demographics respond to certain variables? For example, you might want to run a customer study to see how buyers in different job functions respond to new product features or price changes. Are all groups as enthusiastic about the new features and likely to buy? Or do they have reservations? This kind of data will help inform your overall product strategy and potentially how you tier solutions.
Validate existing conditions
When you have a belief or hypothesis but need to prove it, you can use descriptive techniques to ascertain underlying patterns or assumptions.
Form new hypotheses
With the data presented and surmised in a way that everyone can understand (and infer connections from), you can delve deeper into specific data points to uncover deeper and more meaningful insights — or run more comprehensive research.
Guiding your survey design to improve the data collected
To use your surveys as an effective tool for customer engagement and understanding, every survey goal and item should answer one simple, yet highly important question:
What am I really asking?
It might seem trivial, but by having this question frame survey research, it becomes significantly easier for researchers to develop the right questions that uncover useful, meaningful and actionable insights.
Planning becomes easier, questions clearer and perspective far wider and yet nuanced.
Hypothesize – what’s the problem that you’re trying to solve? Far too often, organizations collect data without understanding what they’re asking, and why they’re asking it.
Finally, focus on the end result. What kind of data do you need to answer your question? Also, are you asking a quantitative or qualitative question? Here are a few things to consider:
- Clear questions are clear for everyone. It takes time to make a concept clear
- Ask about measurable, evident and noticeable activities or behaviors.
- Make rating scales easy. Avoid long lists, confusing scales or “don’t know” or “not applicable” options.
- Ensure your survey makes sense and flows well. Reduce the cognitive load on respondents by making it easy for them to complete the survey.
- Read your questions aloud to see how they sound.
- Pretest by asking a few uninvolved individuals to answer.
Furthermore…
As well as understanding what you’re really asking, there are several other considerations for your data:
Keep it random
How you select your sample is what makes your research replicable and meaningful. Having a truly random sample helps prevent bias, increasingly the quality of evidence you find.
Plan for and avoid sample error
Before starting your research project, have a clear plan for avoiding sample error. Use larger sample sizes, and apply random sampling to minimize the potential for bias.
Don’t over sample
Remember, you can sample 500 respondents selected randomly from a population and they will closely reflect the actual population 95% of the time.
Think about the mode
Match your survey methods to the sample you select. For example, how do your current customers prefer communicating? Do they have any shared characteristics or preferences? A mixed-method approach is critical if you want to drive action across different customer segments.
Use a survey tool that supports you with the whole process
Surveys created using a survey research software can support researchers in a number of ways:
- Employee satisfaction survey template
- Employee exit survey template
- Customer satisfaction (CSAT) survey template
- Ad testing survey template
- Brand awareness survey template
- Product pricing survey template
- Product research survey template
- Employee engagement survey template
- Customer service survey template
- NPS survey template
- Product package testing survey template
- Product features prioritization survey template
These considerations have been included in Qualtrics’ survey software , which summarizes and creates visualizations of data, making it easy to access insights, measure trends, and examine results without complexity or jumping between systems.
Uncover your next breakthrough idea with Stats iQ™
What makes Qualtrics so different from other survey providers is that it is built in consultation with trained research professionals and includes high-tech statistical software like Qualtrics Stats iQ .
With just a click, the software can run specific analyses or automate statistical testing and data visualization. Testing parameters are automatically chosen based on how your data is structured (e.g. categorical data will run a statistical test like Chi-squared), and the results are translated into plain language that anyone can understand and put into action.
Get more meaningful insights from your data
Stats iQ includes a variety of statistical analyses, including: describe, relate, regression, cluster, factor, TURF, and pivot tables — all in one place!
Confidently analyze complex data
Built-in artificial intelligence and advanced algorithms automatically choose and apply the right statistical analyses and return the insights in plain english so everyone can take action.
Integrate existing statistical workflows
For more experienced stats users, built-in R code templates allow you to run even more sophisticated analyses by adding R code snippets directly in your survey analysis.
Advanced statistical analysis methods available in Stats iQ
Regression analysis – Measures the degree of influence of independent variables on a dependent variable (the relationship between two or multiple variables).
Analysis of Variance (ANOVA) test – Commonly used with a regression study to find out what effect independent variables have on the dependent variable. It can compare multiple groups simultaneously to see if there is a relationship between them.
Conjoint analysis – Asks people to make trade-offs when making decisions, then analyses the results to give the most popular outcome. Helps you understand why people make the complex choices they do.
T-Test – Helps you compare whether two data groups have different mean values and allows the user to interpret whether differences are meaningful or merely coincidental.
Crosstab analysis – Used in quantitative market research to analyze categorical data – that is, variables that are different and mutually exclusive, and allows you to compare the relationship between two variables in contingency tables.
Go from insights to action
Now that you have a better understanding of descriptive statistics in research and how you can leverage statistical analysis methods correctly, now’s the time to utilize a tool that can take your research and subsequent analysis to the next level.
Try out a Qualtrics survey software demo so you can see how it can take you through descriptive research and further research projects from start to finish.
Related resources
Market intelligence 10 min read, marketing insights 11 min read, ethnographic research 11 min read, qualitative vs quantitative research 13 min read, qualitative research questions 11 min read, qualitative research design 12 min read, primary vs secondary research 14 min read, request demo.
Ready to learn more about Qualtrics?

IMAGES
COMMENTS
Using the data from these three rows, we can draw the following descriptive picture. Mentabil scores spanned a range of 50 (from a minimum score of 85 to a maximum score of 135). Speed scores had a range of 16.05 s (from 1.05 s - the fastest quality decision to 17.10 - the slowest quality decision).
Similarly, De scriptive statistics are used to summarize and analyze data in. a variety of academic areas, including psychology, sociology, economics, education, and epidemiology [3 ]. Descriptive ...
Descriptive statistics is a powerful beast of burden: (1) It co llects and summarize s vast amounts of data and. information in a manageable and organized manner, (2) A fairly straightforward ...
Descriptive statistics are specific methods basically used to calculate, describe, and summarize collected research data in a logical, meaningful, and efficient way. Descriptive statistics are reported numerically in the manuscript text and/or in its tables, or graphically in its figures. This basic …
In this paper, we present essential methods of Descriptive Statistics for biomedical science students and professionals. We explore data summary techniques such as the mean, median, and mode ...
Types of descriptive statistics. There are 3 main types of descriptive statistics: The distribution concerns the frequency of each value. The central tendency concerns the averages of the values. The variability or dispersion concerns how spread out the values are. You can apply these to assess only one variable at a time, in univariate ...
Abstract. Descriptive statistics provide an essential foundation for understanding and summarizing large datasets by offering valuable insights into the central tendencies, dispersion, and shape of the distribution. By leveraging measures such as mean, median, mode, range, variance, and standard deviation, researchers can succinctly present the ...
Descriptive statistics, although relatively simple, are a critically important part of any quantitative data analysis. Measures of central tendency include the mean (average), median and mode. Skewness indicates whether a dataset leans to one side or another. Measures of dispersion include the range, variance and standard deviation.
Kim Nimon, PhD, is associate professor in the Department of Human Resource Development at The University of Texas at Tyler.Her areas of expertise are in workforce development and quantitative analytical methods. She was awarded the Early Career Scholar Award by the Academy of Human Resource Development in 2013 and the Highly Commended Paper by Emerald Publishing in 2015 and currently serves as ...
Furthermore, the statistical terminology and methods used that comprise descriptive statistics are explained, including levels of measurement, measures of central tendency (average), and dispersion (spread) and the concept of normal distribution. This paper reviews relevant literature, provides a checklist of points to consider before ...
This paper reviews the use of descriptive statistics to describe the participants included in a study. It discusses the practicalities of incorporating statistics in papers for publication in Age and Aging, concisely and in ways that are easy for readers to understand and interpret. older people, descriptive statistics, study participants ...
Mainly descriptive statistics is used to describe the behavior of a. sample data. It is used to present quantitative analysis of the given set of data. As in a study there. are numerous variables ...
Usually there is no good way to write a statistic. It rarely sounds good, and often interrupts the structure or flow of your writing. Oftentimes the best way to write descriptive statistics is to be direct. If you are citing several statistics about the same topic, it may be best to include them all in the same paragraph or section.
Descriptive statistics involves summarizing and organizing data so that they can be easily understood. Even though these are basic and simple concepts, many applied science students have misconceptions about their use in applied experiments in the laboratory. Students usually receive limited or no training in how to understand the meaning of the results obtained from statistical calculations ...
Univariate (crosstabulations are bivariate); descriptive. Purpose : To produce an efficient counting summary of a sample of data points for ease of interpretation. Measurement level : Any level of measurement can be used for a variable summarised in frequency tabulations and crosstabulations.
Descriptive statistics provide a summary of data in the form of mean, median and mode. Inferential statistics use a random sample of data taken from a population to describe and make inferences about the whole population. It is valuable when it is not possible to examine each member of an entire population. The examples if descriptive and ...
Example 1: Student Grades. Let's say a teacher has the following set of grades for 7 students: 85, 90, 88, 92, 78, 88, and 94. The teacher could use descriptive statistics to summarize this data: Median (middle value): First, rearrange the grades in ascending order (78, 85, 88, 88, 90, 92, 94). The median grade is 88.
Measures of Central Tendency and Other Commonly Used Descriptive Statistics. The mean, median, and the mode are all measures of central tendency. They attempt to describe what the typical data point might look like. In essence, they are all different forms of 'the average.'. When writing statistics, you never want to say 'average' because it is ...
Abstract. This short "snippet" covers three important aspects related to statistics - the concept of variables, the importance, and practical aspects related to descriptive statistics and issues related to sampling - types of sampling and sample size estimation. Keywords: Biostatistics, descriptive statistics, sample size, variables.
Descriptive statistics are an important part of biomedical research which is used to describe the basic features of the data in the study. They provide simple summaries about the sample and the measures. Measures of the central tendency and dispersion are used to describe the quantitative data. For the continuous data, test of the normality is ...
The descriptive data analysis tool will help generate summaries about the data samples, whereas inferential statistics would help infer meaning relationships and conclusions regarding the ...
We recommend that researchers report an estimate of informativeness whenever they present descriptive evi-dence as support for structural estimates. Section 6 implements our proposal for three recent papers in economics, each of which reports or discusses descriptive statistics alongside structural estimates.
We call this process "describing data". In the process of producing summaries of the sample, we use measures like mean, median, variance, graphs, charts, frequencies, histograms, box and whisker plots, and percentages. For datasets with just one variable, we use univariate descriptive statistics. For datasets with multiple variables, we use ...
Qualitative research collects data qualitatively, and the method of analysis is also primarily qualitative. This often involves an inductive exploration of the data to identify recurring themes, patterns, or concepts and then describing and interpreting those categories. Of course, in qualitative research, the data collected qualitatively can ...