hypothesis accuracy in machine learning

Evaluating Hypotheses: Estimating hypotheses Accuracy

For estimating hypothesis accuracy, statistical methods are applied. In this blog, we’ll have a look at evaluating hypotheses and estimating it’s accuracy. 

Evaluating hypotheses: 

Whenever you form a hypothesis for a given training data set, for example, you came up with a hypothesis for the EnjoySport example where the attributes of the instances decide if a person will be able to enjoy their favorite sport or not. 

Now to test or evaluate how accurate the considered hypothesis is we use different statistical measures. Evaluating hypotheses is an important step in training the model. 

To evaluate the hypotheses precisely focus on these points: 

When statistical methods are applied to estimate hypotheses, 

• First, how well does this estimate the accuracy of a hypothesis across additional examples, given the observed accuracy of a hypothesis over a limited sample of data?
• Second, how likely is it that if one theory outperforms another across a set of data, it is more accurate in general?
• Third, what is the best strategy to use limited data to both learn and measure the accuracy of a hypothesis?

Motivation: 

There are instances where the accuracy of the entire model plays a huge role in the model is adopted or not. For example, consider using a training model for Medical treatment. We need to have a high accuracy so as to depend on the information the model provides. 

When we need to learn a hypothesis and estimate its future accuracy based on a small collection of data, we face two major challenges:

Bias in the estimation

There is a bias in the estimation. Initially, the observed accuracy of the learned hypothesis over training instances is a poor predictor of its accuracy over future cases.

Because the learned hypothesis was generated from previous instances, future examples will likely yield a skewed estimate of hypothesis correctness.

Estimation variability.  

Second, depending on the nature of the particular set of test examples, even if the hypothesis accuracy is tested over an unbiased set of test instances independent of the training examples, the measurement accuracy can still differ from the true accuracy. 

The anticipated variance increases as the number of test examples decreases.

When evaluating a taught hypothesis, we want to know how accurate it will be at classifying future instances.

Also, to be aware of the likely mistake in the accuracy estimate. There is an X-dimensional space of conceivable scenarios. We presume that different instances of X will be met at different times. 

Assume there is some unknown probability distribution D that describes the likelihood of encountering each instance in X. This is a convenient method to model this.

A trainer draws each instance separately, according to the distribution D, and then passes the instance x together with its correct target value f (x) to the learner as training examples of the target function f.

The following two questions are of particular relevance to us in this context, 

• What is the best estimate of the accuracy of h over future instances taken from the same distribution, given a hypothesis h and a data sample containing n examples picked at random according to the distribution D?
• What is the margin of error in this estimate of accuracy?

True Error and Sample Error: 

We must distinguish between two concepts of accuracy or, to put it another way, error. One is the hypothesis’s error rate based on the available data sample. 

The hypothesis’ error rate over the complete unknown distribution D of examples is the other. These will be referred to as the sampling error and real error, respectively.

The fraction of S that a hypothesis misclassifies is the sampling error of a hypothesis with respect to some sample S of examples selected from X.

Sample Error:

It is denoted by error s (h) of hypothesis h with respect to target function f and data sample S is 

Where n is the number of examples in S, and the quantity  is 1 if f(x) != h(x), and 0 otherwise. 

True Error: 

It is denoted by error D (h) of hypothesis h with respect to target function f and distribution D, which is the probability that h will misclassify an instance drawn at random according to D.

Confidence Intervals for Discrete-Valued Hypotheses:

“How accurate are error s (h) estimates of error D (h)?” – in the case of a discrete-valued hypothesis (h).

To estimate the true error for a discrete-valued hypothesis h based on its observed sample error over a sample S, where

• According to the probability distribution D, the sample S contains n samples drawn independently of one another and of h. 
• Over these n occurrences, hypothesis h commits r mistakes error s (h) = r/n

Under these circumstances, statistical theory permits us to state the following:

• If no additional information is available, the most likely value of error D (h) is error s (h).
• The genuine error error D (h) lies in the interval with approximately 95% probability.

A more precise rule of thumb is that the approximation described above works well when

• Python for Data Science
• Data Analysis
• Machine Learning
• Deep Learning
• Deep Learning Interview Questions
• ML Projects
• ML Interview Questions

Understanding Hypothesis Testing

Hypothesis testing is a fundamental statistical method employed in various fields, including data science , machine learning , and statistics , to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously evaluating these assumptions against collected data. At its core, hypothesis testing is a systematic approach that allows researchers to assess the validity of a statistical claim about an unknown population parameter. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

Table of Content

What is Hypothesis Testing?

Why do we use hypothesis testing, one-tailed and two-tailed test, what are type 1 and type 2 errors in hypothesis testing, how does hypothesis testing work, real life examples of hypothesis testing, limitations of hypothesis testing.

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

To test the validity of the claim or assumption about the population parameter:

• A sample is drawn from the population and analyzed.
• The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

This structured approach to hypothesis testing in data science , hypothesis testing in machine learning , and hypothesis testing in statistics is crucial for making informed decisions based on data.

• By employing hypothesis testing in data analytics and other fields, practitioners can rigorously evaluate their assumptions and derive meaningful insights from their analyses.
• Understanding hypothesis generation and testing is also essential for effectively implementing statistical hypothesis testing in various applications.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

Understanding hypothesis testing in statistics is essential for data scientists and machine learning practitioners, as it provides a structured framework for statistical hypothesis generation and testing. This methodology can also be applied in hypothesis testing in Python , enabling data analysts to perform robust statistical analyses efficiently. By employing techniques such as multiple hypothesis testing in machine learning , researchers can ensure more reliable results and avoid potential pitfalls associated with drawing conclusions from statistical tests. 

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

To delve deeper into differences into both types of test: Refer to link

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

Step 1: Define Null and Alternative Hypothesis

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

Although hypothesis testing is a useful technique in data science , it does not offer a comprehensive grasp of the topic being studied.

• Lack of Comprehensive Insight : Hypothesis testing in data science often focuses on specific hypotheses, which may not fully capture the complexity of the phenomena being studied.
• Dependence on Data Quality : The accuracy of hypothesis testing results relies heavily on the quality of available data. Inaccurate data can lead to incorrect conclusions, particularly in hypothesis testing in machine learning .
• Overlooking Patterns : Sole reliance on hypothesis testing can result in the omission of significant patterns or relationships in the data that are not captured by the tested hypotheses.
• Contextual Limitations : Hypothesis testing in statistics may not reflect the broader context, leading to oversimplification of results.
• Complementary Methods Needed : To gain a more holistic understanding, it’s essential to complement hypothesis testing with other analytical approaches, especially in data analytics and data mining .
• Misinterpretation Risks : Poorly formulated hypotheses or inappropriate statistical methods can lead to misinterpretation, emphasizing the need for careful consideration in hypothesis testing in Python and related analyses.
• Multiple Hypothesis Testing Challenges : Multiple hypothesis testing in machine learning poses additional challenges, as it can increase the likelihood of Type I errors, requiring adjustments to maintain validity.

Hypothesis testing is a cornerstone of statistical analysis , allowing data scientists to navigate uncertainties and draw credible inferences from sample data. By defining null and alternative hypotheses, selecting significance levels, and employing statistical tests, researchers can validate their assumptions effectively.

This article emphasizes the distinction between Type I and Type II errors, highlighting their relevance in hypothesis testing in data science and machine learning . A practical example involving a paired T-test to assess a new drug’s effect on blood pressure underscores the importance of statistical rigor in data-driven decision-making .

Ultimately, understanding hypothesis testing in statistics , alongside its applications in data mining , data analytics , and hypothesis testing in Python , enhances analytical frameworks and supports informed decision-making.

Understanding Hypothesis Testing- FAQs

What is hypothesis testing in data science.

In data science, hypothesis testing is used to validate assumptions or claims about data. It helps data scientists determine whether observed patterns are statistically significant or could have occurred by chance.

How does hypothesis testing work in machine learning?

In machine learning, hypothesis testing helps assess the effectiveness of models. For example, it can be used to compare the performance of different algorithms or to evaluate whether a new feature significantly improves a model’s accuracy.

What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

What is the difference between hypothesis testing and data mining?

Hypothesis testing focuses on evaluating specific claims or hypotheses about a dataset, while data mining involves exploring large datasets to discover patterns, relationships, or insights without predefined hypotheses.

How is hypothesis generation used in business analytics?

In business analytics , hypothesis generation involves formulating assumptions or predictions based on available data. These hypotheses can then be tested using statistical methods to inform decision-making and strategy.

What is the significance level in hypothesis testing?

The significance level, often denoted as alpha (α), is the threshold for deciding whether to reject the null hypothesis. Common significance levels are 0.05, 0.01, and 0.10, indicating the probability of making a Type I error in statistical hypothesis testing .

Similar Reads

• Data Analysis with Python In this article, we will discuss how to do data analysis with Python. We will discuss all sorts of data analysis i.e. analyzing numerical data with NumPy, Tabular data with Pandas, data visualization Matplotlib, and Exploratory data analysis.  Data Analysis With Python Data Analysis is the technique 15+ min read

Introduction to Data Analysis

• What is Data Analysis? Data analysis is an essential aspect of modern decision-making processes across various sectors, including business, healthcare, finance, and academia. As organizations generate massive amounts of data daily, understanding how to extract meaningful insights from this data becomes crucial. In this ar 13 min read
• Data Analytics and its type Data analytics is an important field that involves the process of collecting, processing, and interpreting data to uncover insights and help in making decisions. Data analytics is the practice of examining raw data to identify trends, draw conclusions, and extract meaningful information. This involv 9 min read
• How to Install Numpy on Windows? Python NumPy is a general-purpose array processing package that provides tools for handling n-dimensional arrays. It provides various computing tools such as comprehensive mathematical functions, and linear algebra routines. NumPy provides both the flexibility of Python and the speed of well-optimiz 3 min read
• How to Install Pandas in Python? Pandas in Python is a package that is written for data analysis and manipulation. Pandas offer various operations and data structures to perform numerical data manipulations and time series. Pandas is an open-source library that is built over Numpy libraries. Pandas library is known for its high pro 5 min read
• How to Install Matplotlib on python? Matplotlib is an amazing visualization library in Python for 2D plots of arrays. Matplotlib is a multi-platform data visualization library built on NumPy arrays and designed to work with the broader SciPy stack. In this article, we will look into the various process of installing Matplotlib on Windo 2 min read
• How to Install Python Tensorflow in Windows? Tensorflow is a free and open-source software library used to do computational mathematics to build machine learning models more profoundly deep learning models. It is a product of Google built by Google’s brain team, hence it provides a vast range of operations performance with ease that is compati 3 min read

Data Analysis Libraries

• Pandas Tutorial Pandas is an open-source library that is built on top of NumPy library. Pandas is mainly popular for importing and analyzing data much easier. Pandas is a Python library for data analysis and manipulation, with high-level data structures like Series and DataFrame.Ensures compatibility with numerical 15+ min read
• NumPy Tutorial - Python Library NumPy is a general-purpose array-processing Python library which provides handy methods/functions for working n-dimensional arrays. NumPy is a short form for "Numerical Python". It provides various computing tools such as comprehensive mathematical functions, and linear algebra routines. NumPy provi 8 min read
• Data Analysis with SciPy Scipy is a Python library useful for solving many mathematical equations and algorithms. It is designed on the top of Numpy library that gives more extension of finding scientific mathematical formulae like Matrix Rank, Inverse, polynomial equations, LU Decomposition, etc. Using its high-level funct 6 min read
• Introduction to TensorFlow TensorFlow is an open-source machine learning library developed by Google. TensorFlow is used to build and train deep learning models as it facilitates the creation of computational graphs and efficient execution on various hardware platforms. The article provides an comprehensive overview of tensor 11 min read

Data Visulization Libraries

• Matplotlib Tutorial Matplotlib is easy to use and an amazing visualizing library in Python. It is built on NumPy arrays and designed to work with the broader SciPy stack and consists of several plots like line, bar, scatter, histogram, etc. In this article, you'll gain a comprehensive understanding of the diverse range 8 min read
• Python Seaborn Tutorial Seaborn is a library mostly used for statistical plotting in Python. It is built on top of Matplotlib and provides beautiful default styles and color palettes to make statistical plots more attractive. In this tutorial, we will learn about Python Seaborn from basics to advance using a huge dataset o 15+ min read
• Plotly tutorial Plotly library in Python is an open-source library that can be used for data visualization and understanding data simply and easily. Plotly supports various types of plots like line charts, scatter plots, histograms, box plots, etc. So you all must be wondering why Plotly is over other visualization 15+ min read
• Introduction to Bokeh in Python Bokeh is a Python interactive data visualization. Unlike Matplotlib and Seaborn, Bokeh renders its plots using HTML and JavaScript. It targets modern web browsers for presentation providing elegant, concise construction of novel graphics with high-performance interactivity. Features of Bokeh: Some o 1 min read

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis In this article,we will be discussing univariate, bivariate, and multivariate data and their analysis. Univariate data: Univariate data refers to a type of data in which each observation or data point corresponds to a single variable. In other words, it involves the measurement or observation of a s 5 min read
• Measures of Central Tendency in Statistics Central Tendencies in Statistics are the numerical values that are used to represent mid-value or central value a large collection of numerical data. These obtained numerical values are called central or average values in Statistics. A central or average value of any statistical data or series is th 10 min read
• Measures of Spread - Range, Variance, and Standard Deviation Collecting the data and representing it in form of tables, graphs, and other distributions is essential for us. But, it is also essential that we get a fair idea about how the data is distributed, how scattered it is, and what is the mean of the data. The measures of the mean are not enough to descr 9 min read
• Interquartile Range and Quartile Deviation using NumPy and SciPy In statistical analysis, understanding the spread or variability of a dataset is crucial for gaining insights into its distribution and characteristics. Two common measures used for quantifying this variability are the interquartile range (IQR) and quartile deviation. Quartiles Quartiles are a kind 6 min read
• Anova Formula ANOVA Test, or Analysis of Variance, is a statistical method used to test the differences between means of two or more groups. Developed by Ronald Fisher in the early 20th century, ANOVA helps determine whether there are any statistically significant differences between the means of three or more in 7 min read
• Skewness of Statistical Data Skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. In simpler terms, it indicates whether the data is concentrated more on one side of the mean compared to the other side. Why is skewness important?Understanding the skewness of dat 5 min read
• How to Calculate Skewness and Kurtosis in Python? Skewness is a statistical term and it is a way to estimate or measure the shape of a distribution. It is an important statistical methodology that is used to estimate the asymmetrical behavior rather than computing frequency distribution. Skewness can be two types: Symmetrical: A distribution can be 3 min read
• Difference Between Skewness and Kurtosis What is Skewness? Skewness is an important statistical technique that helps to determine the asymmetrical behavior of the frequency distribution, or more precisely, the lack of symmetry of tails both left and right of the frequency curve. A distribution or dataset is symmetric if it looks the same t 4 min read
• Histogram | Meaning, Example, Types and Steps to Draw What is Histogram?A histogram is a graphical representation of the frequency distribution of continuous series using rectangles. The x-axis of the graph represents the class interval, and the y-axis shows the various frequencies corresponding to different class intervals. A histogram is a two-dimens 5 min read
• Interpretations of Histogram Histograms helps visualizing and comprehending the data distribution. The article aims to provide comprehensive overview of histogram and its interpretation. What is Histogram?Histograms are graphical representations of data distributions. They consist of bars, each representing the frequency or cou 7 min read
• Box Plot Box Plot is a graphical method to visualize data distribution for gaining insights and making informed decisions. Box plot is a type of chart that depicts a group of numerical data through their quartiles. In this article, we are going to discuss components of a box plot, how to create a box plot, u 7 min read
• Quantile Quantile plots The quantile-quantile( q-q plot) plot is a graphical method for determining if a dataset follows a certain probability distribution or whether two samples of data came from the same population or not. Q-Q plots are particularly useful for assessing whether a dataset is normally distributed or if it 8 min read
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation? Data Visualisation is a graphical representation of information and data. By using different visual elements such as charts, graphs, and maps data visualization tools provide us with an accessible way to find and understand hidden trends and patterns in data. In this article, we are going to see abo 3 min read
• Using pandas crosstab to create a bar plot In this article, we will discuss how to create a bar plot by using pandas crosstab in Python. First Lets us know more about the crosstab, It is a simple cross-tabulation of two or more variables. What is cross-tabulation? It is a simple cross-tabulation that help us to understand the relationship be 3 min read
• Exploring Correlation in Python This article aims to give a better understanding of a very important technique of multivariate exploration. A correlation Matrix is basically a covariance matrix. Also known as the auto-covariance matrix, dispersion matrix, variance matrix, or variance-covariance matrix. It is a matrix in which the 4 min read
• Covariance and Correlation Covariance and correlation are the two key concepts in Statistics that help us analyze the relationship between two variables. Covariance measures how two variables change together, indicating whether they move in the same or opposite directions. In this article, we will learn about the differences 6 min read
• Factor Analysis | Data Analysis Factor analysis is a statistical method used to analyze the relationships among a set of observed variables by explaining the correlations or covariances between them in terms of a smaller number of unobserved variables called factors. Table of Content What is Factor Analysis?What does Factor mean i 13 min read
• Data Mining - Cluster Analysis INTRODUCTION: Cluster analysis, also known as clustering, is a method of data mining that groups similar data points together. The goal of cluster analysis is to divide a dataset into groups (or clusters) such that the data points within each group are more similar to each other than to data points 8 min read
• MANOVA Test in R Programming Multivariate analysis of variance (MANOVA) is simply an ANOVA (Analysis of variance) with several dependent variables. It is a continuation of the ANOVA. In an ANOVA, we test for statistical differences on one continuous dependent variable by an independent grouping variable. The MANOVA continues th 4 min read
• Python - Central Limit Theorem Central Limit Theorem (CLT) is a foundational principle in statistics, and implementing it using Python can significantly enhance data analysis capabilities. Statistics is an important part of data science projects. We use statistical tools whenever we want to make any inference about the population 7 min read
• Probability Distribution Function Probability Distribution refers to the function that gives the probability of all possible values of a random variable.It shows how the probabilities are assigned to the different possible values of the random variable.Common types of probability distributions Include: Binomial Distribution.Bernoull 9 min read
• Probability Density Estimation & Maximum Likelihood Estimation Probability density and maximum likelihood estimation (MLE) are key ideas in statistics that help us make sense of data. Probability Density Function (PDF) tells us how likely different outcomes are for a continuous variable, while Maximum Likelihood Estimation helps us find the best-fitting model f 8 min read
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions The exponential distribution in R Language is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. In R Programming Langu 2 min read
• Mathematics | Probability Distributions Set 4 (Binomial Distribution) The previous articles talked about some of the Continuous Probability Distributions. This article covers one of the distributions which are not continuous but discrete, namely the Binomial Distribution. Introduction - To understand the Binomial distribution, we must first understand what a Bernoulli 5 min read
• Poisson Distribution | Definition, Formula, Table and Examples The Poisson distribution is a type of discrete probability distribution that calculates the likelihood of a certain number of events happening in a fixed time or space, assuming the events occur independently and at a constant rate. It is characterized by a single parameter, λ (lambda), which repres 11 min read
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret A p-value is a statistical metric used to assess a hypothesis by comparing it with observed data. This article delves into the concept of p-value, its calculation, interpretation, and significance. It also explores the factors that influence p-value and highlights its limitations. Table of Content W 12 min read
• Z-Score in Statistics | Definition, Formula, Calculation and Uses Z-Score in statistics is a measurement of how many standard deviations away a data point is from the mean of a distribution. A z-score of 0 indicates that the data point's score is the same as the mean score. A positive z-score indicates that the data point is above average, while a negative z-score 15+ min read
• How to Calculate Point Estimates in R? Point estimation is a technique used to find the estimate or approximate value of population parameters from a given data sample of the population. The point estimate is calculated for the following two measuring parameters: Measuring parameterPopulation ParameterPoint EstimateProportionπp Meanμx̄ T 3 min read
• Confidence Interval In the realm of statistics, precise estimation is paramount to drawing meaningful insights from data. One of the indispensable tools in this pursuit is the confidence interval. Confidence intervals provide a systematic approach to quantifying the uncertainty associated with sample statistics, offeri 12 min read
• Chi-square test in Machine Learning Chi-Square test is a statistical method crucial for analyzing associations in categorical data. Its applications span various fields, aiding researchers in understanding relationships between factors. This article elucidates Chi-Square types, steps for implementation, and its role in feature selecti 11 min read
• Understanding Hypothesis Testing Hypothesis testing is a fundamental statistical method employed in various fields, including data science, machine learning, and statistics, to make informed decisions based on empirical evidence. It involves formulating assumptions about population parameters using sample statistics and rigorously 15+ min read

Data Preprocessing

• ML | Data Preprocessing in Python In order to derive knowledge and insights from data, the area of data science integrates statistical analysis, machine learning, and computer programming. It entails gathering, purifying, and converting unstructured data into a form that can be analysed and visualised. Data scientists process and an 7 min read
• ML | Overview of Data Cleaning Data cleaning is one of the important parts of machine learning. It plays a significant part in building a model. In this article, we'll understand Data cleaning, its significance and Python implementation. What is Data Cleaning?Data cleaning is a crucial step in the machine learning (ML) pipeline, 15 min read
• ML | Handling Missing Values Missing values are a common issue in machine learning. This occurs when a particular variable lacks data points, resulting in incomplete information and potentially harming the accuracy and dependability of your models. It is essential to address missing values efficiently to ensure strong and impar 12 min read
• Detect and Remove the Outliers using Python Outliers, deviating significantly from the norm, can distort measures of central tendency and affect statistical analyses. The piece explores common causes of outliers, from errors to intentional introduction, and highlights their relevance in outlier mining during data analysis. The article delves 10 min read

Data Transformation

• Data Normalization Machine Learning Normalization is an essential step in the preprocessing of data for machine learning models, and it is a feature scaling technique. Normalization is especially crucial for data manipulation, scaling down, or up the range of data before it is utilized for subsequent stages in the fields of soft compu 9 min read
• Sampling distribution Using Python There are different types of distributions that we study in statistics like normal/gaussian distribution, exponential distribution, binomial distribution, and many others. We will study one such distribution today which is Sampling Distribution. Let's say we have some data then if we sample some fin 3 min read

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data Data mining refers to extracting or mining knowledge from large amounts of data. In other words, Data mining is the science, art, and technology of discovering large and complex bodies of data in order to discover useful patterns. Theoreticians and practitioners are continually seeking improved tech 3 min read
• Basic DateTime Operations in Python Python has an in-built module named DateTime to deal with dates and times in numerous ways. In this article, we are going to see basic DateTime operations in Python. There are six main object classes with their respective components in the datetime module mentioned below: datetime.datedatetime.timed 12 min read
• Time Series Analysis & Visualization in Python Every dataset has distinct qualities that function as essential aspects in the field of data analytics, providing insightful information about the underlying data. Time series data is one kind of dataset that is especially important. This article delves into the complexities of time series datasets, 11 min read
• How to deal with missing values in a Timeseries in Python? It is common to come across missing values when working with real-world data. Time series data is different from traditional machine learning datasets because it is collected under varying conditions over time. As a result, different mechanisms can be responsible for missing records at different tim 10 min read
• How to calculate MOVING AVERAGE in a Pandas DataFrame? Calculating the moving average in a Pandas DataFrame is used for smoothing time series data and identifying trends. The moving average, also known as the rolling mean, helps reduce noise and highlight significant patterns by averaging data points over a specific window. In Pandas, this can be achiev 7 min read
• What is a trend in time series? Time series data is a sequence of data points that measure some variable over ordered period of time. It is the fastest-growing category of databases as it is widely used in a variety of industries to understand and forecast data patterns. So while preparing this time series data for modeling it's i 3 min read
• How to Perform an Augmented Dickey-Fuller Test in R Augmented Dickey-Fuller Test: It is a common test in statistics and is used to check whether a given time series is at rest. A given time series can be called stationary or at rest if it doesn't have any trend and depicts a constant variance over time and follows autocorrelation structure over a per 3 min read
• AutoCorrelation Autocorrelation is a fundamental concept in time series analysis. Autocorrelation is a statistical concept that assesses the degree of correlation between the values of variable at different time points. The article aims to discuss the fundamentals and working of Autocorrelation. Table of Content Wh 10 min read

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects Did you think data is only for big companies and corporations to analyze and obtain business insights? No, data is also fun! There is nothing more interesting than analyzing a data set to find the correlations between the data and obtain unique insights. It’s almost like a mystery game where the dat 7 min read
• Step by Step Predictive Analysis - Machine Learning Predictive analytics involves certain manipulations on data from existing data sets with the goal of identifying some new trends and patterns. These trends and patterns are then used to predict future outcomes and trends. By performing predictive analysis, we can predict future trends and performanc 3 min read
• 6 Tips for Creating Effective Data Visualizations The reality of things has completely changed, making data visualization a necessary aspect when you intend to make any decision that impacts your business growth. Data is no longer for data professionals; it now serves as the center of all decisions you make on your daily operations. It's vital to e 6 min read
• Data Science
• data-science

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Hypothesis in Machine Learning

October 30, 2024

Anshuman Singh

Latest articles

Top 25 data science companies in india in 2025, a complete data science career guide, top 13 data science programming languages in 2025, difference between big data and data science, data science fundamentals, top 10 benefits of data science in 2025, what is data exploration a complete guide, locally weighted linear regression.

Machine learning involves building models that learn from data to make predictions or decisions. A hypothesis plays a crucial role in this process by serving as a candidate solution or function that maps input data to desired outputs. Essentially, a hypothesis is an assumption made by the learning algorithm about the relationship between features (input data) and target values (output). The goal of machine learning is to find the best hypothesis that performs well on unseen data.

This article will explore the concept of hypothesis in machine learning, covering its formulation, representation, evaluation, and importance in building reliable models. We will also differentiate between hypotheses in machine learning and statistical hypothesis testing, offering a clear understanding of how these concepts differ.

What is Hypothesis?

​​In simple terms, a hypothesis is an assumption or a possible solution that explains the relationship between inputs and outputs in a model. It’s like a mathematical function that predicts the target value (output) for given input data.

In machine learning, the hypothesis is different from a statistical hypothesis .

• It is a function learned by the model to map input data to predicted outputs.
• For example, in a linear regression model, the hypothesis might be: y=mx+c, where mmm and ccc are parameters learned during training.
• This refers to an assumption about a population parameter, like testing whether two means are equal.

While both involve assumptions, in machine learning, the hypothesis focuses on learning patterns from data, whereas in statistics, it focuses on testing assumptions about data.

How does a Hypothesis work?

In machine learning, a hypothesis functions as a possible mapping between input data and output values. The process of selecting and refining a hypothesis involves several steps and concepts:

• The hypothesis space is the set of all possible hypotheses (functions) the algorithm can choose from. For example, in linear regression, the space includes all linear equations of the form y=mx+cy = mx + cy=mx+c.
• Each learning algorithm defines its own hypothesis space, such as decision trees , neural networks , or linear models .
• A hypothesis is selected based on the given data and the type of learning algorithm.
• For example, a neural network might formulate a complex function with multiple hidden layers, while a decision tree divides the input space into distinct regions based on conditions.
• The algorithm searches through the hypothesis space to find the hypothesis that performs best on the training data. This is done by minimizing errors using methods like gradient descent.
• The goal is to identify the hypothesis that not only fits the training data but also generalizes well to unseen data.

Hypothesis Space and Representation in Machine Learning

The hypothesis space refers to the collection of all possible hypotheses (functions) that a learning algorithm can select from to solve a problem. This space defines the boundaries within which the model searches for the best hypothesis to fit the data.

1. Hypothesis Space Definition

• In mathematical terms, it is denoted as H, where each element in H is a possible hypothesis. For example, in linear regression, the space includes all linear functions like y=mx+c.

2. Types of Hypothesis Spaces Based on Algorithms

• Linear Models: The hypothesis space contains linear equations that map input features to output values.
• Decision Trees: The space includes different ways of splitting data to form a tree, with each tree structure representing a unique hypothesis.
• Neural Networks: The space consists of various architectures (e.g., different numbers of layers or nodes), with each configuration being a potential hypothesis.

3. Balancing Complexity and Simplicity:

• A larger hypothesis space provides flexibility but increases the risk of overfitting . Conversely, a smaller hypothesis space may limit the model’s performance and lead to underfitting .
• The choice of hypothesis space is closely related to model selection , as it influences how well the model can capture patterns in data.

Hypothesis Formulation and Representation in Machine Learning

The process of formulating a hypothesis involves defining a function that reflects the relationship between input data and output predictions. This formulation is influenced by the nature of the problem, the dataset, and the choice of learning algorithm.

1. Steps in Formulating a Hypothesis:

• Understand the Problem: Identify the type of task—classification, regression, or clustering.
• Select an Algorithm: Choose an appropriate algorithm (e.g., linear regression for predicting continuous values or decision trees for classification).
• For example, in linear regression: y=mx+c
• In a decision tree, the hypothesis takes the form of conditional rules (e.g., “If income > 50K, then class = high”).

2. Role of Model Selection:

• Choosing the right model helps define the hypothesis space. Models like support vector machines , neural networks , or k-nearest neighbors use different types of functions as hypotheses.

3. Hyperparameter Tuning in Formulating Hypotheses:

• Hyperparameters, such as learning rate or tree depth , affect the hypothesis by controlling how the model learns patterns. Proper tuning ensures that the selected hypothesis generalizes well to new data.

Hypothesis Evaluation

Once a hypothesis is formulated, it must be evaluated to determine how well it fits the data. This evaluation helps assess whether the chosen hypothesis is appropriate for the task and if it generalizes well to unseen data.

1. Role of Loss Function:

• A loss function measures the difference between the predicted output and the actual output.
• Mean Squared Error (MSE): Used for regression tasks to measure average squared differences between predictions and actual values.
• Cross-Entropy Loss: Applied in classification tasks to assess the difference between predicted probabilities and actual labels.

2. Performance Metrics:

• Accuracy: For classification tasks.
• Precision and Recall: For imbalanced datasets.
• R² Score: For regression models to measure how well predictions align with actual data.

3. Iterative Improvement:

• If the initial hypothesis does not perform well, the learning algorithm iteratively updates it to minimize the loss. This is done through optimization techniques like gradient descent .

Hypothesis Testing and Generalization

In machine learning, testing a hypothesis is crucial to ensure the model not only fits the training data but also performs well on new, unseen data. This concept is closely tied to generalization —the ability of a model to maintain performance across different datasets.

1. Overfitting and Underfitting:

• Overfitting: The model learns patterns, including noise, from the training data, leading to poor performance on new data.
• Underfitting: The model is too simplistic and fails to capture the underlying patterns in the data, resulting in low accuracy on both training and test data.

2. Techniques to Avoid Overfitting and Underfitting:

• Regularization: Adds penalties to the model’s complexity to prevent overfitting (e.g., L1 and L2 regularization).
• Cross-Validation: Splits the dataset into multiple subsets to ensure the model generalizes well to unseen data.

3. The Importance of Generalization:

• A hypothesis that generalizes well offers reliable predictions and works effectively in real-world scenarios.
• Learning algorithms aim to strike a balance between underfitting and overfitting, ensuring the model learns meaningful patterns without becoming too complex.

Hypothesis in Statistics

In statistics, a hypothesis refers to an assumption or claim about a population parameter. Unlike the hypothesis in machine learning, which focuses on making predictions, statistical hypotheses are tested to determine whether they hold true based on sample data.

• It states that there is no significant difference or relationship between variables (e.g., “There is no difference in the average heights of men and women”).
• It contradicts the null hypothesis and suggests that there is a significant difference or relationship (e.g., “The average height of men is different from that of women”).

How Hypothesis Testing Differs from Machine Learning Hypothesis Evaluation:

• Involves accepting or rejecting the null hypothesis based on evidence from sample data.
• Uses p-values and significance levels to determine whether the results are statistically significant.
• Focuses on finding the best hypothesis (model function) that maps inputs to outputs.
• Evaluates performance using loss functions and cross-validation rather than statistical significance.

Significance Level

In statistical hypothesis testing, the significance level (denoted as α ) is the threshold used to determine whether to reject the null hypothesis. It indicates the probability of rejecting the null hypothesis when it is actually true (Type I error).

• 0.05 (5%) : This is the most commonly used level, meaning there is a 5% risk of incorrectly rejecting the null hypothesis.
• 0.01 (1%) : Used in cases where stronger evidence is required.
• 0.10 (10%) : In some exploratory studies, a higher significance level is accepted.

How Significance Level Works:

• If the p-value (calculated from the test) is less than or equal to the significance level (α) , the null hypothesis is rejected, indicating the result is statistically significant.
• If the p-value is greater than α, there is not enough evidence to reject the null hypothesis.

The p-value is a crucial concept in statistical hypothesis testing that helps determine the strength of the evidence against the null hypothesis (H₀) . It represents the probability of obtaining a test result at least as extreme as the one observed, assuming the null hypothesis is true.

• A small p-value (≤ α) indicates strong evidence against the null hypothesis, leading to its rejection.
• A large p-value (> α) suggests weak evidence against the null hypothesis, meaning we fail to reject it.
• If the significance level (α) is 0.05 and the p-value is 0.03 , the result is considered statistically significant, and we reject the null hypothesis.
• If the p-value is 0.07 , we do not reject the null hypothesis at the 0.05 significance level.

In machine learning, a hypothesis is a function that maps inputs to outputs. The process of formulating and evaluating hypotheses is key to building models that generalize well. Concepts like hypothesis space , overfitting , and loss functions guide the selection of the best hypothesis.

Unlike statistical hypothesis testing, which evaluates assumptions about data, machine learning hypotheses focus on learning patterns for prediction. Mastering these concepts ensures better model performance, making hypothesis formulation a crucial part of any machine learning project.

Featured articles

December 19, 2024

Pruning in Machine Learning

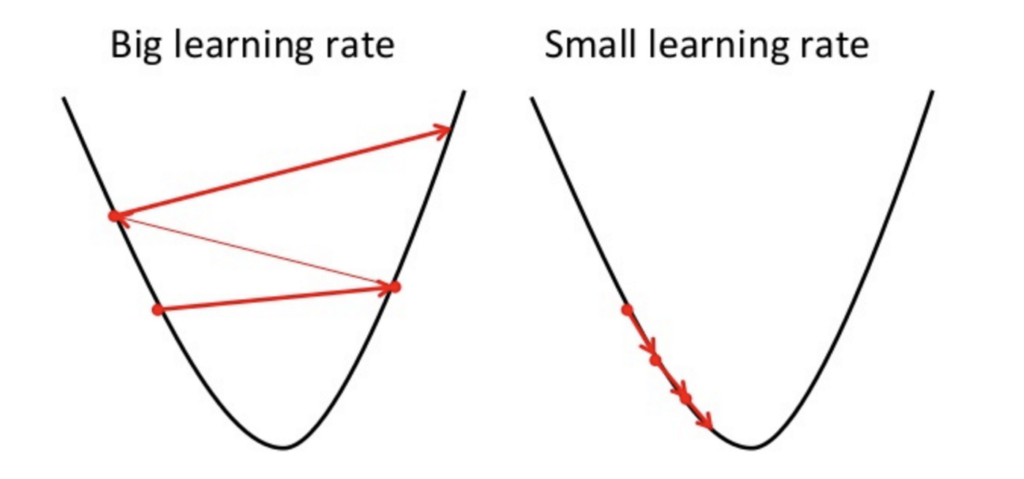
Learning Rate in Machine Learning

Mohit Uniyal

December 17, 2024

Goals of Artificial Intelligence

Team Applied AI

Evaluating Hypotheses in Machine Learning: A Comprehensive Guide

Learn how to evaluate hypotheses in machine learning, including types of hypotheses, evaluation metrics, and common pitfalls to avoid. Improve your ML model's performance with this in-depth guide.

Create an image featuring JavaScript code snippets and interview-related icons or graphics. Use a color scheme of yellows and blues. Include the title '7 Essential JavaScript Interview Questions for Freshers'.

🎉 Exclusive Deal Alert! 17 premium courses for just ₹999.

Introduction.

Machine learning is a crucial aspect of artificial intelligence that enables machines to learn from data and make predictions or decisions. The process of machine learning involves training a model on a dataset, and then using that model to make predictions on new, unseen data. However, before deploying a machine learning model, it is essential to evaluate its performance to ensure that it is accurate and reliable. One crucial step in this evaluation process is hypothesis testing.

In this blog post, we will delve into the world of hypothesis testing in machine learning, exploring what hypotheses are, why they are essential, and how to evaluate them. We will also discuss the different types of hypotheses, common pitfalls to avoid, and best practices for hypothesis testing.

What are Hypotheses in Machine Learning?

In machine learning, a hypothesis is a statement that proposes a possible explanation for a phenomenon or a problem. It is a conjecture that is made about a population parameter, and it is used as a basis for further investigation. In the context of machine learning, hypotheses are used to define the problem that we are trying to solve.

For example, let's say we are building a machine learning model to predict the prices of houses based on their features, such as the number of bedrooms, square footage, and location. A possible hypothesis could be: "The price of a house is directly proportional to its square footage." This hypothesis proposes a possible relationship between the price of a house and its square footage.

Why are Hypotheses Essential in Machine Learning?

Hypotheses are essential in machine learning because they provide a framework for understanding the problem that we are trying to solve. They help us to identify the key variables that are relevant to the problem, and they provide a basis for evaluating the performance of our machine learning model.

Without a clear hypothesis, it is difficult to develop an effective machine learning model. A hypothesis helps us to:

• Identify the key variables that are relevant to the problem
• Develop a clear understanding of the problem that we are trying to solve
• Evaluate the performance of our machine learning model
• Refine our model and improve its accuracy

Types of Hypotheses in Machine Learning

There are two main types of hypotheses in machine learning: null hypotheses and alternative hypotheses.

Null Hypothesis

A null hypothesis is a hypothesis that proposes that there is no significant difference or relationship between variables. It is a hypothesis of no effect or no difference. For example, let's say we are building a machine learning model to predict the prices of houses based on their features. A null hypothesis could be: "There is no significant relationship between the price of a house and its square footage."

Alternative Hypothesis

An alternative hypothesis is a hypothesis that proposes that there is a significant difference or relationship between variables. It is a hypothesis of an effect or a difference. For example, let's say we are building a machine learning model to predict the prices of houses based on their features. An alternative hypothesis could be: "There is a significant positive relationship between the price of a house and its square footage."

Evaluating Hypotheses in Machine Learning

Evaluating hypotheses in machine learning involves testing the null hypothesis against the alternative hypothesis. This is typically done using statistical methods, such as t-tests, ANOVA, and regression analysis.

Here are the general steps involved in evaluating hypotheses in machine learning:

• Formulate the null and alternative hypotheses : Clearly define the null and alternative hypotheses that you want to test.
• Collect and prepare the data : Collect the data that you will use to test the hypotheses. Ensure that the data is clean, relevant, and representative of the population.
• Choose a statistical method : Select a suitable statistical method to test the hypotheses. This could be a t-test, ANOVA, regression analysis, or another method.
• Test the hypotheses : Use the chosen statistical method to test the null hypothesis against the alternative hypothesis.
• Interpret the results : Interpret the results of the hypothesis test. If the null hypothesis is rejected, it suggests that there is a significant relationship between the variables. If the null hypothesis is not rejected, it suggests that there is no significant relationship between the variables.

Common Pitfalls to Avoid in Hypothesis Testing

Here are some common pitfalls to avoid in hypothesis testing:

• Overfitting : Overfitting occurs when a model is too complex and performs well on the training data but poorly on new, unseen data. To avoid overfitting, use techniques such as regularization, early stopping, and cross-validation.
• Underfitting : Underfitting occurs when a model is too simple and fails to capture the underlying patterns in the data. To avoid underfitting, use techniques such as feature engineering, hyperparameter tuning, and model selection.
• Data leakage : Data leakage occurs when the model is trained on data that it will also be tested on. To avoid data leakage, use techniques such as cross-validation and walk-forward optimization.
• P-hacking : P-hacking occurs when a researcher selectively reports the results of multiple hypothesis tests to find a significant result. To avoid p-hacking, use techniques such as preregistration and replication.

Best Practices for Hypothesis Testing in Machine Learning

Here are some best practices for hypothesis testing in machine learning:

• Clearly define the hypotheses : Clearly define the null and alternative hypotheses that you want to test.
• Use a suitable statistical method : Choose a suitable statistical method to test the hypotheses.
• Use cross-validation : Use cross-validation to evaluate the performance of the model on unseen data.
• Avoid overfitting and underfitting : Use techniques such as regularization, early stopping, and feature engineering to avoid overfitting and underfitting.
• Document the results : Document the results of the hypothesis test, including the statistical method used, the results, and any conclusions drawn.

Evaluating hypotheses is a crucial step in machine learning that helps us to understand the problem that we are trying to solve and to evaluate the performance of our machine learning model. By following the best practices outlined in this blog post, you can ensure that your hypothesis testing is rigorous, reliable, and effective.

Remember to clearly define the null and alternative hypotheses, choose a suitable statistical method, and avoid common pitfalls such as overfitting, underfitting, data leakage, and p-hacking. By doing so, you can develop machine learning models that are accurate, reliable, and effective.

• [1] James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: With Applications in R. Springer.
• [2] Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
• [3] Han, J., Pei, J., & Kamber, M. (2012). Data Mining: Concepts and Techniques. Morgan Kaufmann.

I hope this helps! Let me know if you need any further assistance.