how to find speed of sound in air experiment

Seven experiments to measure the speed of sound in the air

Updated: Feb 15

Calculating the speed of sound becomes a simple and engaging task with the use of a smartphone, transforming this commonly abstract concept into a tangible learning experience. For students, this exercise is particularly gratifying as it demystifies the complexities of sound waves, allowing them to explore its various physical properties through a device that's a familiar staple in their everyday lives. In this article, we introduce seven experiments, each utilizing a smartphone and the FizziQ app , to determine the speed of sound, making science interactive and accessible.

Sound waves and their propagation - Methods for measuring the speed of sound - Measurement by time of flight - Measurement by wavelength - Measurement by resonance frequency - Conclusion

Sound waves and their propagation

A sound wave is a mechanical vibration that propagates through a medium, such as air or a liquid. The speed of sound is the speed at which this wave propagates in this m edium, it depends on the temperature, the pressure and the density of the medium through which it propagates. In air, if we assimilate it to a perfect diatomic gas, we can calculate the speed of sound by the equation: c = sqrt(γ*RT/Ma), c, the speed of sound, γ, the ratio of heat capacities at constant pressure and volume. γ= 7/5 for air, R, the ideal gas constant, T, the absolute temperature of the medium, Ma, the molar mass of air: Ma = 29g/mol. Using the previous formula we can calculate the theoretical speed of sound at the usual conditions of temperature and pressure: c = 343 m/s for a temperature of 20 degrees, or approximately 767 miles per hour. In water, sound travels more than 4 times faster than in air, i.e. at about 1,482 meters per second, and in some metals like soft iron, it travels significantly faster at close to 6,000 m/s (13,333 miles per hour).

How to measure the speed of sound with a smartphone?

There are many different ways to measure the speed of sound using a smartphone or a tablet. These methods fall into three broad categories, which, interestingly, use different physical characteristics of sound waves :

Estimating the time of flight (ToF )

Measuring the sound frequency using an Helmholtz resonator

Measuring the wavelength at a given frequency

These are the methods that have been used by generations of scientists to determine the speed of sound:

➡️ Marin Mersenne, the first, evaluated in 1635 the speed of sound in air at 448 m/s by the propagation time method. Value further refined by the scientists Viviani and Borelli in 1656 with a value of 344 m/s.

➡️ Isaac Newton took a different approach through an analytical method by determining it from the resonant frequencies of sound waves in a U-tube and details his method in the first edition ofIt begins (1687).

➡️ Over the centuries, as estimations were more accurate, one uncertainty remained: could humans go faster than the speed of sound? This question will be resolved in 1947 when American aviator Chuck Yeager reached Mach 1 aboard the X-1 aircraft . Once again, the human had crossed an impassable barrier.

Now, the iconic measurement of the speed of sound is readily accessible to anyone. You can delve into these experiments using one or more smartphones, with no need for specialized equipment. Embark on a journey of discovery right at your fingertips, grab your cellphones and let's dive into this exciting venture!

Measuring the Time of Flight (ToF)

Like any speed calculation, the objective here is to determine the time it takes for a sound wave to travel a certain distance . The speed of sound being high, the measurement of time requires a specific equipment: an acoustic stopwatch.

An acoustic stopwatch measures the time difference between two sounds which sound level exceeds a certain threshold. This device cannot be found on a lab bench but many smartphone applications exist that offer this functionality. In FizziQ, you will find the acoustic stopwatch in the Tools menu. You can also build your own acoustic stopwatch using triggers .

The traditional protocol for measuring the speed of sound with an acoustic stopwatch is as follows: two smartphones are separated by a certain distance (at least 5 meters), and an operator is placed near each telephone. The operators clap their hands one after the other. The first clap starts both stopwatch and the seconds stops them. Students then check that the time difference dt between the two stopwatches is dt = 2*d/c, where d is the distance between the smartphones, c the speed of sound. This experiment allows an accuracy between 5 and 10%, and can be improved by performing several measurements. An opportunity to do a bit of statistics as well !

The protocol works well, but younger students find it often difficult to understand the offset formula calculation which is not very intuitive. We prefer a variation of this protocol developed by Aline Chaillou of the La main à la pâte Foundation.

In this second protocol, we start by synchronizing the chronometers by putting them side by side and trigger the sound chronometers by clapping our hands. Then, we move one of the two smartphone by a certain distance d without making noise. An operator located near this second laptop then stops the two stopwatches by clapping his hands. The calculation of the shift is then very intuitive for the students because they have immediately put in relation the difference in distance which creates the phase shift with the displacement of one of the two smartphones.

The time difference dt is equal to: dt = d/c.

This second protocol also makes it possible to introduce the notion of clock synchronization. It is the same concept of synchronization that was used in the famous Hafele-Keating experiment in 1971 to prove relativity. Be mindful to calibrate the trigger level of the sound stopwatch so that it does not trigger when you move one of the two smartphones.

Watch our vidéo :

Measuring the speed of sound with Helmholtz resonators

The second method of calculating the speed of sound is based on the principle of acoustic resonance, which is a phenomenon in which an acoustic system amplifies sound waves whose frequency corresponds to one of its own frequencies of vibration. The resonance frequencies of certain cavities like a cylinders or a bottles are easy to determine by calculus. This frequency depends on the speed of sound and the shape of the object. By measuring the resonance frequency we can infer the speed of sound.

A very simple first protocol consists of blowing on the edge of a graduated test tube. This emits a sound for which we can measure the fundamental frequency using FizziQ. For a closed tube, the fundamental resonance frequency is: f₀ = c(4*L+1.6*D), where L is the length of the tube, D is the diameter of the tube.

To make more precise measurements, we can measure the frequency for different heights of water in the test piece, and by doing a linear regression of the results, we can accurately determine the speed of sound to less than one percent.

If you are a Bordeaux lover and have an empty bottle, you can use a bottle from this region whose volumetric characteristics are immutable. Ulysse Delabre in this video details the calculations for measuring the resonance frequency when blowing into the bottle.

What if the bottle is unopened? It is still possible to carry out the experiment and, paradoxically, in an even simpler way: by uncorking it! When the cork is removed, a "pop" is heard which is due to the resonance of the air in the part between the liquid and the top of the bottle. If we measure the frequency of pop with the frequency meter, we can use the previous formula of the resonant frequency of a tube to deduce the speed of sound.

A last protocol which always surprises students uses the fact that if several frequencies are emitted simultaneously in a cavity, the harmonics of the resonant frequency of the cavity will be amplified compared to the other emitted frequencies. If we measure the spectrum of a white noise emitted in this cavity, the harmonic frequencies of the resonant frequency are highlighted compared to the others. It is recalled that white noise is a random succession of sound emitted in all frequencies. White noise sounds can be found in FizziQ's sound library.

So let's take a tube open at both ends, such as a paper towel roll or a vacuum cleaner hose. At one end of the tube, we will emit a white noise that can be generated with the FizziQ sound library or by using the sound of a video emitting white or pink noise. At the other end of the tube, we measure the frequency spectrum. Measuring the white noise spectrum through a tube will show peaks for the fundamental frequency and its harmonics. We deduce the resonance frequency then the speed of sound by the formula of the resonance frequency of an open tube :  f₀ = c(2*L+1.6*D)

Better results are often obtained with pink noise, which is similar to white noise, but with a reduced loudness for high-pitched sounds. The use of pink noise makes it possible to reinforce the intensity of the fundamental resonant frequency compared to its higher harmonics. Examples of of pink noise can be found on internet.

Finally, one can make different measurements with different sizes of the tube, and deduce c by measuring the slope on the graph.

Measuring the speed of sound with waves interferences

This third type of protocol is based on measuring the wavelength of a pure sound of known frequency. We deduce the speed by the relation: c = l.f, with l the wavelength and f the frequency.

This method is the one usually used in the school labs. It uses a sound source and two microphones placed at a certain distance from this source and connected to an oscilloscope with a dual input. By moving the two microphones relative to each other, the operator finds the distance for which the two waves are in phase, which is the wavelength.

With smartphones, this protocol is not possible because they do not have dual sound inputs... However with a little imagination we can find other ways!

The first protocol that we propose consists in using two smartphones that emit the same pure sound, for example at a frequency of 680 hertz. By placing the smartphones at a certain distance, we will calculate the places along the two smartphones axis where waves add up and places where they cance.

With FizziQ one can use the sound at 680 hertz from the sound library. Two smartphones are placed about 3 meters from each other. A third smartphone is used to measure the sound intensity (oscillogram instrument on FizziQ) along the axis of the two smartphones.  The interference of the two waves creates zones of very high intensities, the antinodes, and other very weak ones, the nodes. The distance between the nodes (about 50 cm) is equal to the wavelength of the sound wave for the frequency 680 hertz. By measuring the difference between the nodes (or the bellies), we calculate the speed of sound.

This experience also opens an interesting discussion on how active noise reduction headphones work by carrying out a small activity: https://www.fizziq.org/en/team/noise-cancellation  

The experiment can also be carried out with only two mobile phones.  One of the two smartphones then serves as a transmitter, and also as a tool for measuring the sound volume. A second mobile that emits a pure sound of the same frequency is approached to the first, and the distance between the knot and the belly is noted by measuring the sound volume on the first smartphone, identified by the variations in intensity. To carry out this experiment with FizziQ, we prefer to use the sound intensity measured with the Oscilloscope instrument and which is more precise than the sound volume in decibels.

Finally, if you only have a smartphone, it is also possible to carry out this experiment by placing a reflective surface in place of the second smartphone  from the previous experiment. The precision is further reduced but the calculation is nevertheless possible!

These different experiments make it possible to calculate the speed of sound with an accuracy of about 10%.

To conclude

We have identified a number of different ways to estimate the speed of sound. These experiments can be classified into three categories that relate to different physical properties of sound waves. All of these experiments can be done with FizziQ, or with other mobile or tablet apps, depending on your preference. The smartphone is one of the best tools available for measuring the speed of sound, offering multiple ways to approach the same problem, and easily accessible to students. Happy experimenting!

Recent Posts

Seven Experiments on Gravity with your Smartphone

Measuring Pi with Smartphone Sensors: A Fun and Educational Challenge

5 science projects in biomechanics with a smartphone

2 comentarios

where is the seventh one u liarrrrrr

Hi Beau, you are right, there are eight experiments 🔬 rather than seven ! 2 on time of travel, 3 for interferences, and 3 for Helmholtz resonator 👍

Talk to our experts

1800-120-456-456

To Find the Speed of Sound in Air at Room Temperature Using a Resonance Tube

Physics Experiment - To Find the Speed of Sound in Air at Room Temperature Using a Resonance Tube by two Resonance Positions

Resonance is a special case of the forced vibration. For resonance to occur, the frequency of externally applied periodic force on the system should be equal to its natural frequency. Resonance increases the amplitude of a vibrating object. Resonance is also useful for tuning a radio receiver to the desired frequency, increasing the intensity of sound in musical instruments and analysing musical notes. We can find the speed of sound using the resonance phenomenon with the help of a resonance tube experiment.

Table of Contents:

Apparatus required, observations, precautions.

Lab Manual Questions

Viva Questions

Practical based questions.

To find the speed of sound in air at room temperature using a resonance tube by two resonance positions

Water in a beaker

Resonance tube

Set squares

Thermometer

Two tuning forks of known frequency

We know that when a vibrating tuning fork of known frequency $\nu $ is held over the top of an air column in a glass tube, we can get a standing wave pattern in the glass tube.

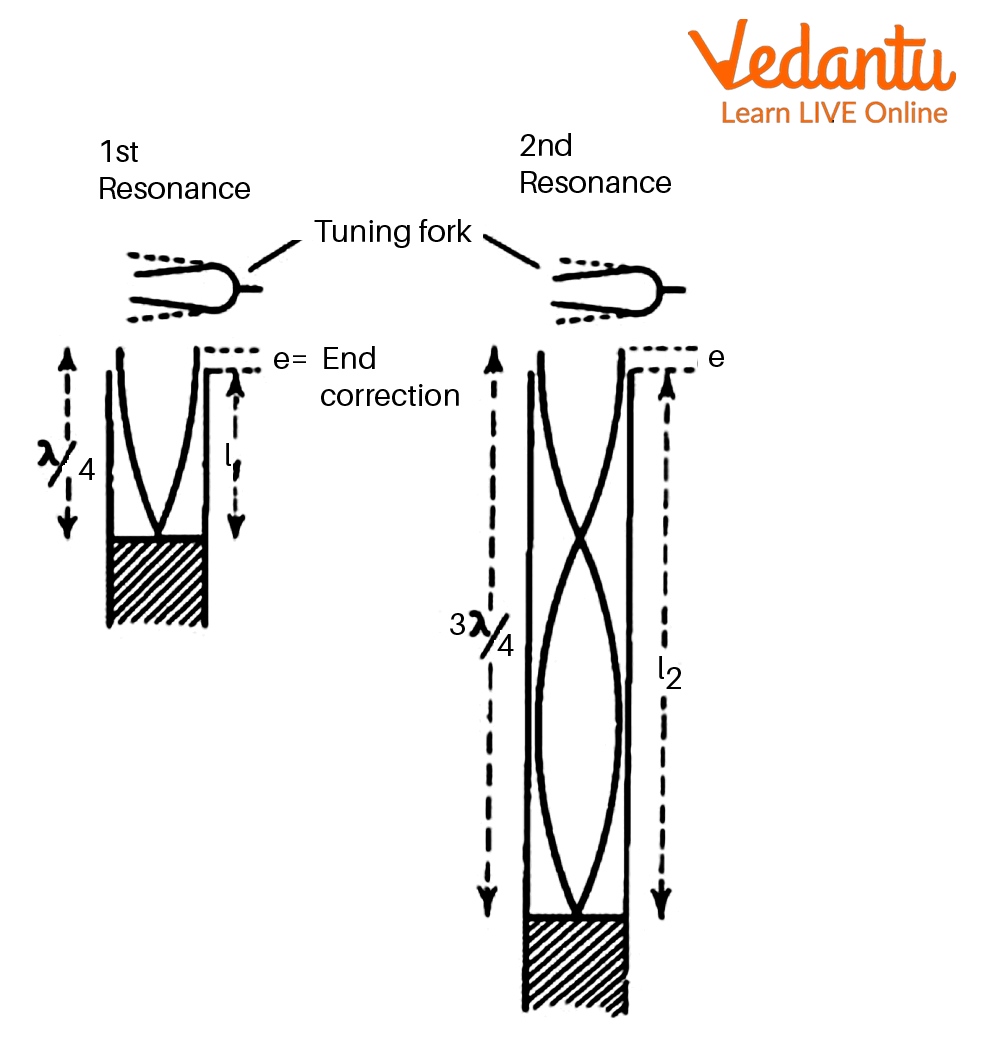
Formation of Standing Wave in Glass Tube

In a closed organ pipe like a resonance tube , there should be a zero amplitude point at the closed end. For resonance, an antinode must be formed at the open end, and a node must be formed at the closed end. Suppose the first loud sound is heard at length ${l_1}$ of the air column. When the natural frequency of the air column of length ${l_1}$ becomes equal to the natural frequency of the tuning fork, it can vibrate with the maximum amplitude. As we can see from the above figure, the length of the air column vibrating is slightly longer than the air column in the resonance tube .

For the first resonance,

$\dfrac{\lambda }{4} = {l_1} + e$

Where, $e$ is the end correction for the resonance tube, and it should be equal to $0.6r$, where $r$ = radius of the glass tube

$\lambda $ is the wavelength of the sound which is produced with the help of the tuning fork.

Now on further lowering the closed end of the tube, let the second resonance position be heard at length ${l_2}$ of the air column in the tube. This ${l_2}$ would equal approximately three-quarters of the wavelength shown in the above figure.

So, for the second resonance,

$\dfrac{{3\lambda }}{4} = {l_2} + e$

Subtract equation (ii) from equation (i),

${l_2} - {l_1} = \dfrac{\lambda }{2}$

Therefore, $\lambda  = 2\left( {{l_2} - {l_1}} \right)$

We know that velocity of sound $v = \nu \lambda $

Substituting the value of $\lambda $ in the above equation, we will get,

$v = \nu [2\left( {{l_2} - {l_1}} \right)]$

So, velocity is $v = 2\nu \left( {{l_2} - {l_1}} \right)$

First of all, set the resonance tube vertical by making the base horizontal, with the help of levelling screws and spirit level and note the room temperature with the help of a thermometer.

Experimental Setup

Now, note the frequency of the given tuning fork and then fix the reservoir in the uppermost position of the vertical rod with the help of a clamp.

Now, fill the reservoir with water with a beaker so that the tube's water level reaches its open end. Now, tighten the pinch cock and lower the position of the reservoir.

After doing this, take a tuning fork, gently strike it on a rubber pad, and put it nearly 1 cm above the open end of the tube. 

Now, keep both the prongs parallel to the ground so that the prongs can vibrate in the vertical plane and try to listen to the sound produced in the tube. This sound may not be audible in this position. 

Then, slowly loosen the pinch cock so that the water level falls in the tube very slowly and keep bringing the tuning fork near the open end of the resonance tube and notice the increasing loudness of the sound.

Repeat the above three steps till we get the exact position of the water level in the tube for which the intensity of sound becomes maximum (which is being produced in the tube). 

If the air column length is minimum, this corresponds to the first resonance position or fundamental node. Now, we need to close the pinch cock at this position and note this position of water level or length ${l_1}$ of the air column in the tube. In this way, we can determine the first resonance position while the water level is falling in the tube.

Repeat the above steps to confirm the first resonance position. 

Then, find out the first resonance position by gradually raising the level of water in the tube and holding the vibrating tuning fork continuously on the top of its open end and fix the tube at the position where the sound of maximum intensity is heard.

Now, to determine the second resonance position, lower the position of the water level further in the resonance tube by sliding down the position of the reservoir on the vertical stand and opening the pinch cock till the length of the air column in the tube increases about three times of the length ${l_1}$

Now, find out the second resonance position and determine the length of air column ${l_2}$ in the resonance tube with the same tuning fork having frequency ${\nu _1}$ and confirm the length ${l_2}$ by taking four readings, two when the level of water is falling and the other two when the level of water is rising in the resonance tube . 

Repeat the above steps with a second tuning fork having frequency ${\nu _2}$ and determine the first and second resonance positions, and we should calculate the sound velocity in each case. 

Temperature of the room $\theta $ = _____ $^\circ C$

Frequency of first tuning fork ${\nu _1}$ = _____ $Hz$

Frequency of second tuning fork ${\nu _2}$ = _____ $Hz$

Frequency of first tuning fork is ${\nu _1}$ = _____ $Hz$ 

Velocity of sound in air can be calculated as ${v_1} = 2{\nu _1}\left( {{l_2} - {l_1}} \right)$ = _____ $m{s^{ - 1}}$ 

Frequency for second tuning fork is ${\nu _2}$ = _____ $Hz$

So, velocity of sound in air can be calculated as, ${v_2} = 2{\nu _2}\left( {{l_2} - {l_1}} \right)$ = _____ $m{s^{ - 1}}$ 

So, the mean velocity of sound $v$ in air at room temperature can be calculated by, 

$v = \dfrac{{{v_1} + {v_2}}}{2}$ $m{s^{ - 1}}$ 

The velocity of sound in air (at room temperature) is $v = \dfrac{{{v_1} + {v_2}}}{2}$ = _____ $m{s^{ - 1}}$ 

We should keep the resonance tube vertical using the levelling screws.

To identify the resonance positions properly, we should perform this experiment in a quiet atmosphere.

Resonance tube which we are using to perform this experiment must be of a uniform area of cross-section. 

Lab Manual Questions 

1. What have forced vibrations?

Ans: When an object is made to vibrate with an external periodic force different from the object's natural frequency, then that object's vibrations are called forced vibrations.

2. Write one possible error that can affect the result of this experiment.

Ans: The humidity above the enclosed water column can increase sound velocity. This is the possible error that can affect the final result of this experiment. 

3. What is a tuning fork? 

Ans: A tuning fork is the simplest source of the sound. It consists of a U-shaped bar of metal with arms of exactly equal length and mass and with a stem provided in the middle. It freely vibrates on its resonance frequency.

4. What is the resonance tube's operating principle?

Ans: The resonance of an air column with a tuning fork is the basis for the resonance tube. In the air column, stationary transverse waves form. The wave's node is at the water's surface, and its antinode is at the open end of the tube.

1. On what principle does the resonance tube work?

Ans: The resonance tube works on the principle of the air column with a tuning fork.

2. Is there a node or antinode at the open end of the water level in this experiment?

Ans: It is an antinode at the open end of the water level in this experiment.

3. Do we find the velocity of sound in the air column or the water column?

Ans: We find the sound velocity in the air column above the water column.

4. On what principle does the guitar work?

Ans: Guitar works on the principle of resonance of sound.

5. What type of waves can we produce in the air column?

Ans: We can produce longitudinal stationary waves in the air column. 

6. Will we get different results if we take liquids other than water?

Ans: We will get the same result if we take liquids other than water.

7. What is the meaning of the frequency of the tuning fork?

Ans: The number of vibrations completed by a prong of the tuning fork per second is called the frequency of the tuning fork.

8. Is there a node or antinode at the close end of the water level in this experiment? 

Ans: It is a node at the open end of the water level in this experiment.

What happens to the resonance position if we use kerosene oil in place of water in this experiment?

Remains unchanged

Becomes almost zero

Ans: Option C - Remains unchanged 

The velocity of sound in air (at room temperature) is directly proportional to the _____

Wavelength of light

Square root of temperature (in Kelvin)

Intensity of magnetic field

Frequency of light

Ans: Option B - Square root of temperature (in Kelvin)

We can produce sound with the help of _____ object.

Ans: Option D - Vibrating

In which of the following medium speed of sound would be maximum?

None of the above

Ans: Option C - Steel

Sound travels slowest in _____

Solids 

Ans: Option C - Gases

The speed of sound in distilled water is _____ the speed of sound in oxygen.

Greater than

Ans: Option A - Greater than

Sound waves can not pass through _____

Ans: Option C - Vacuum

We can measure speed of sound in _____

Metre/second

Ans: Option A - Metre/second

Sound waves are _____

Non-mechanical waves

Transverse waves

Longitudinal mechanical waves

Both A and B

Ans: Option C - Longitudinal mechanical waves

SI unit of frequency is

Ans: Option D - Hertz

This experiment was developed to investigate the standing waves in a closed pipe and to determine the speed of sound in air at room temperature. We can conclude from this experiment that

The difference between the theoretical and experimental value of the speed of sound in air at room temperature is very small. 

End correction does not affect the final result of this experiment.

FAQs on To Find the Speed of Sound in Air at Room Temperature Using a Resonance Tube

1. What do we mean by the term resonance?

Resonance is the phenomenon of increased amplitude that occurs when the frequency of applied periodic force is equal to the natural frequency of the system on which it acts.

2. What are forced oscillations?

When the oscillating system is driven by a periodic force external to the oscillating system is known as forced oscillation.

3. Write down the factors on which the velocity of sound depends.

Following are the factors on which the velocity of sound depends. 

Temperature of medium 

Density of air

Humidity of air and wind flow of air

4. State one difference between forced vibrations and resonance.

Forced vibrations are produced by the external periodic force of any frequency while resonance is produced by an external periodic force whose frequency is equal to the natural frequency of the system.