class 9 maths chapter 1 assignment solution

Search This Blog

Featured posts, maths through stories | 17 camels & 3 sons, math assignment class ix ch -1| number system, maths assignment   class 9th chapter 1.

MATHEMATICS ASSIGNMENT CLASS IX  NUMBER SYSTEM

 (a) 1⁸ × 3⁰ × 5³ × 2²           Ans; 500,                

(b)  4 -3 × 4⁸ ÷ 4²                Ans; 64

(d) 3 -4 × 3 -5 ÷ 3¹⁰             Ans; 3 -19

Download complete pdf file 

Plese send us solution today is our test

Need solutions toooo

Post a Comment

Breaking news, popular post on this blog, theorems on quadrilaterals ch-8 class-ix.

Lesson Plan Maths Class 10 | For Mathematics Teacher

Mathematics Class 10 Lab Manual | 21 Lab Activities

• Assignment 10 15
• Assignment 11 13
• Assignment 12 16
• Assignment 8 8
• Assignment 9 5
• Lesson plan 10 15
• Lesson Plan 12 14
• Lesson Plan 8 10
• Maths 10 20
• Maths 11 22
• Maths 12 18
• Story Telling 1

SUBSCRIBE FOR NEW POSTS

Get new posts by email:.

Chapter 1 – Matrices and Determinants

Exercise 1.1, exercise 1.2, exercise 1.3, exercise 1.4, exercise 1.5, exercise 1.6, review exercise, multiple choice questions, this post has 15 comments.

Thank you so much I really appreciate you It really helped me I searched alot but I can’t find any answers Thank you again Good effort 👍

Bro literally everything thing is available here!very weldone bro! Excellent job ❤️❤️

Nice effort!

Please give extra MCQ’S of maths…

This is very good facility for students . We can study from here. I advice to free ilm owner to give math extra m.c.q.s

Thanks bro! this is very helpful for new students of class 9th….

Don’t know how to download offline

Simply, click on [open] link and download it.

where is chapter no 3 q no.3

Its help me alot in my test.

It helps much

Please ask me questions

Thats very nice site.

So i will give you give star

Leave a Reply Cancel reply

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems are provided here. Our NCERT Maths solutions contain all the questions of the NCERT textbook that are solved and explained beautifully. Here you will get complete NCERT Solutions for Class 9 Maths Chapter 1 all exercises Exercise in one place. These solutions are prepared by the subject experts and as per the latest NCERT syllabus and guidelines. CBSE Class 9 Students who wish to score good marks in the maths exam must practice these questions regularly.

Class 9 Maths Chapter 1 Number Systems NCERT Solutions

Below we have provided the solutions of each exercise of the chapter. Go through the links to access the solutions of exercises you want. You should also check out our NCERT Class 9 Solutions for other subjects to score good marks in the exams.

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.1

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.2

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.3

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.4

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.5

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.6

NCERT Solutions for Class 9 Maths Chapter 1 – Topic Discussion

Below we have listed the topics that have been discussed in this chapter. As Number System is one of the important topics in Maths, it has a weightage of 6 marks in class 9 Maths exams. 

• Introduction of Number Systems
• Irrational Numbers
• Real Numbers and Their Decimal Expansions
• Representing Real Numbers on the Number Line.
• Operations on Real Numbers
• Laws of Exponents for Real Numbers

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

Class 9 Maths Chapter 1 Solution for CBSE Board Class 9 Maths Exercise 1.1 in English Class 9 Maths Exercise 1.2 in English Class 9 Maths Exercise 1.3 in English Class 9 Maths Exercise 1.4 in English Class 9 Maths Exercise 1.5 in English

Class 9 Maths Chapter 1 Solution for State Boards Class 9 Maths Chapter 1 Exercise 1.1 Class 9 Maths Chapter 1 Exercise 1.2 Class 9 Maths Chapter 1 Exercise 1.3 Class 9 Maths Chapter 1 Exercise 1.4 Class 9 Maths Chapter 1 Exercise 1.5 Class 9 Maths Chapter 1 Exercise 1.6

Class 9 Maths Chapter 1 Solution in Hindi Class 9 Maths Exercise 1.1 in Hindi Class 9 Maths Exercise 1.2 in Hindi Class 9 Maths Exercise 1.3 in Hindi Class 9 Maths Exercise 1.4 in Hindi Class 9 Maths Exercise 1.5 in Hindi

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems in Hindi Medium and English medium has been updated for academic session 2024-25. Tiwari Academy is a popular online platform that provides educational resources and solutions for students. As we continue to offer Class 9 Maths NCERT Solutions, here are some potential benefits of using Tiwari Academy for learning Class 9 Maths. Question-answers and solutions are modified as per revised NCERT book published for 2024-25 syllabus. We typically provides simple yet complete solutions to NCERT textbooks, including step-by-step explanations for each problem. This can be especially helpful for students who may find difficulty in understanding certain concepts.

All the Solutions for Class 9th Maths Chapter 1 have been updated according to latest CBSE Curriculum and NCERT Books for 2024-25. Since UP Board Students are using same NCERT Textbooks , they can also download UP Board Solutions for Class 9 Maths Chapter 1 in Hindi Medium or English Medium. Class 9 Maths NCERT Solutions have been provided by explaining the formulae and giving step by step explanation.

The content is according to the latest CBSE syllabus 2024-25 for the students of CBSE Board as well as UP Board and MP Board following the updated NCERT (https://ncert.nic.in/) Books for their final exams. Solutions for chapter 1 9th Maths are available in PDF format on our website Tiwari Academy and also through videos on Apps and website.

Study Materials on 9th Maths Chapter 1

• Study Material 9th Maths Chapter 1 for 2024-25 – English Medium
• Study Material 9th Maths Chapter 1 for 2024-25 – Hindi Medium
• Class 9 Mathematics Solutions Main Page

The topic Number Systems is the basis of Arithmetic. It is like learning the alphabets of any mathematics. We can say that 9th Maths chapter 1 is the foundation of Maths for secondary classes. CBSE NCERT Solutions for Class 9 mathematics Chapter 1 Number Systems in PDF format. These solutions are available for free download for session 2024-25. These are updated as per latest curriculum. Kindly visit the Discussion Forum and become a partner in knowledge sharing in mathematics. NCERT Solutions Offline Apps 2024-25, work without internet connection. Everything on Tiwari Academy website and Apps are available free of cost. No login or registration is required.

Important Questions on 9th Maths Chapter 1

Is zero a rational number can you write it in the form p/q, where p and q are integers and q≠0.

Yes, zero is a rational number. It can be written in the form of p/q. For example: 0/1, 0/2, 0/5 are rational numbers, where p and q are integers and q≠0.

Simplify each of the following expression: (3 + √3)(2 + √2)

(3 + √3)(2 + √2) = 6 + 3√2 + 2√3 + √6

Find six rational numbers between 3 and 4.

Six rational numbers between 3 and 4 are 3.1, 3.2, 3.3, 3.4, 3.5 and 3.6.

Express 0.99999… in the form of p/q . Are you surprised by your answer?

0.99999… Let x = 0.99999… … (i) Multiplying equation (i) by 10 both sides 10x = 9.99999… ⇒ 10x = 9 + 0.99999…… ⇒ 10x = 9 + x [From equation (i)] ⇒ 10x – x = 9 ⇒ 9x = 9 ⇒ x = 9/9 = 1 The answer makes sense as 0.99999… is very close to 1, that is why we can say that 0.99999=1.

Write three numbers whose decimal expansions are non-terminating non-recurring.

Three non-terminating non-recurring decimals: 0.414114111411114… 2.01001000100001… π=3.1416…

1. Natural numbers are those numbers which are used for counting. 2. Whole numbers are the collection of all natural numbers together with zero. 3. Integers are the collection of all whole numbers and negative of natural numbers. 4. Rational numbers are those numbers which can be expressed in the form of p/q, where p, q are integers and q is not equal to 0. 5. Irrational numbers are those numbers which cannot be expressed in the form of p/q, where p, q are integers and q is not = 0. 6. Real numbers are the collection of all rational and irrational numbers.

Two numbers are said to be equivalent, if numerators and denominators of both are in proportion or they are reducible to be equal. The decimal expansion of real numbers can be terminating or non-terminating repeating or non-terminating non-repeating. The decimal expansion of rational numbers can either be terminating or non-terminating and vice-versa. The decimal expansion of irrational numbers can either be non-recurring and vice-versa.

If a is a rational and b is an irrational, then a + b and a – b are irrational, and ab and a/b are irrational numbers, where b is not equal to 0. If a and b both are irrational, then a+b, a-b, ab and a/b may be rational or irrational. If a be any real number and n be any positive integer such that a^1/n = n√a is a real number, then ‘n’ is called exponent, a is called radical and √ is called radical sign.

How many questions in each exercise are given in chapter 1 of class 9 Maths?

There are 6 exercises in chapter 1 (Number systems) of class 9 Maths. In the first exercise (Ex 1.1), there are four questions. In the second exercise (Ex 1.2), there are four questions. In the third exercise (Ex 1.3), there are nine questions. In the fifth exercise (Ex 1.4), there are five questions. In the sixth exercise (Ex 1.5), there are three questions. So, there are in all 25 questions in chapter 1 (Number systems) of class 9 Maths. There are in all 20 examples in chapter 1 (Number systems) of class 9 Maths.

What are the core topics to study in chapter 1 Number systems of class 9 Mathematics?

In chapter 1, Number systems of class 9 Maths, students will study: 1. Natural Numbers, Whole Numbers, Integers, Rational Numbers. 2. Irrational Numbers. 3. Real Numbers and their Decimal Expansions. 4. Representing Real Numbers on the Number Line. 5. Operations on Real Numbers. 6. Laws of Exponents for Real Numbers.

Is chapter 1 of class 9th Maths difficult to solve?

Chapter 1 of class 9th Maths is not easy and not difficult. It lies in the middle of easy and difficult because some examples and questions of this chapter are easy, and some are difficult. However, the difficulty level of anything varies from student to student. So, Chapter 1 of class 9th Maths is easy or not depends on students also. Some students find it difficult, some find it easy, and some find it in the middle of easy and difficult.

How long it takes to study chapter 1 of class 9th Maths?

Students need a maximum of eight days to do chapter 1 of class 9th Maths if they give at least 2 hours per day to this chapter. This time also depends on student’s speed, efficiency, capability, and many other factors.

Chapter 2. Polynomials »

Mayank Tiwari

I have completed my M. Tech. in Computer Science and Engineering, Specialization in Artificial Intelligence in Delhi. Since, then I am working for Tiwari Academy as quality manager in Tech and Content formation.

Copyright 2024 by Tiwari Academy | A step towards Free Education

• NCERT Solutions
• NCERT Class 9
• NCERT 9 Maths
• Chapter 1: Number Systems
• Exercise 1.1

NCERT Solutions for class 9 Maths Chapter 1 - Number Systems Exercise 1.1

NCERT Solutions Class 9 Maths Chapter 1 Number Systems Exercise 1.1 are provided here. Our subject experts have prepared the NCERT Maths solutions for Class 9 chapter-wise so that it helps students to solve problems easily while using it as a reference. They also focus on creating solutions for these exercises in such a way that it is easy to understand for the students.

NCERT Solutions for Class 9 Maths Chapter 1- Number Systems Exercise 1.1

carouselExampleControls111

Previous Next

Exercise 1.2 Solutions 4 Questions (3 long and 1 short)

Exercise 1.3 Solutions 9 Questions (9 long)

Exercise 1.4 Solutions 2 Questions (2 long)

Exercise 1.5 Solutions 5 Questions (4 long and 1 short)

Exercise 1.6 Solutions 3 Questions (3 long)

Access Answers to Maths NCERT Class 9 Chapter 1 – Number Systems Exercise 1.1

1. Is zero a rational number? Can you write it in the form p/q where p and q are integers and q ≠ 0?

We know that a number is said to be rational if it can be written in the form p/q , where p and q are integers and q ≠ 0.

Taking the case of ‘0’,

Zero can be written in the form 0/1, 0/2, 0/3 … as well as , 0/1, 0/2, 0/3 ..

Since it satisfies the necessary condition, we can conclude that 0 can be written in the p/q form, where q can either be positive or negative number.

Hence, 0 is a rational number.

2. Find six rational numbers between 3 and 4.

There are infinite rational numbers between 3 and 4.

As we have to find 6 rational numbers between 3 and 4, we will multiply both the numbers, 3 and 4, with 6+1 = 7 (or any number greater than 6)

i.e., 3 × (7/7) = 21/7

and, 4 × (7/7) = 28/7. The numbers between 21/7 and 28/7 will be rational and will fall between 3 and 4.

Hence, 22/7, 23/7, 24/7, 25/7, 26/7, 27/7 are the 6 rational numbers between 3 and 4.

3. Find five rational numbers between 3/5 and 4/5.

There are infinite rational numbers between 3/5 and 4/5.

To find out 5 rational numbers between 3/5 and 4/5, we will multiply both the numbers 3/5 and 4/5

with 5+1=6 (or any number greater than 5)

i.e., (3/5) × (6/6) = 18/30

and, (4/5) × (6/6) = 24/30

The numbers between18/30 and 24/30 will be rational and will fall between 3/5 and 4/5.

Hence, 19/30, 20/30, 21/30, 22/30, 23/30 are the 5 rational numbers between 3/5 and 4/5

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Natural numbers- Numbers starting from 1 to infinity (without fractions or decimals)

i.e., Natural numbers= 1,2,3,4…

Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)

i.e., Whole numbers= 0,1,2,3…

Or, we can say that whole numbers have all the elements of natural numbers and zero.

Every natural number is a whole number; however, every whole number is not a natural number.

(ii) Every integer is a whole number.

Integers- Integers are set of numbers that contain positive, negative and 0; excluding fractional and decimal numbers.

i.e., integers= {…-4,-3,-2,-1,0,1,2,3,4…}

i.e., Whole numbers= 0,1,2,3….

Hence, we can say that integers include whole numbers as well as negative numbers.

Every whole number is an integer; however, every integer is not a whole number.

(iii) Every rational number is a whole number.

Rational numbers- All numbers in the form p/q, where p and q are integers and q≠0.

i.e., Rational numbers = 0, 19/30 , 2, 9/-3, -12/7…

All whole numbers are rational; however, all rational numbers are not whole numbers.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Exercise 1.1 is the first exercise of Chapter 1 of Class 9 Maths. This exercise explains how to find rational numbers between two given numbers.

Key Features of NCERT Solutions for Class 9 Maths Chapter 1 – Number Systems Exercise 1.1

• These NCERT Solutions help you solve and revise all questions of Exercise 1.1.
• After going through the stepwise solutions given by our subject expert teachers, you will be able to score more marks.
• It follows NCERT guidelines which help in preparing the students accordingly.
• It contains all the important questions from the examination point of view.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Talk to our experts

1800-120-456-456

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

• NCERT Solutions
• Chapter 1 Number Systems

NCERT Solutions for Class 9 Maths Chapter 1 Number System - Free PDF 2024-25

Chapter 1 number system class 9 delves into the principles covered under the topic of the number system. Vedantu offers an expert-curated NCERT answer for CBSE Class 9 Chapter 1. To ace your preparations, get the NCERT solution supplied by our professionals. The freely available number system class 9 PDF offers step-by-step solutions to the NCERT practice problems. The NCERT solutions PDF for chapter 1 maths class 9 contains the answers to all the Class 9 maths syllabus questions.

Glance of NCERT Solutions for Class 9 Maths Chapter 1 Number System | Vedantu

Class 9 chapter 1 maths dives into the fundamental building block of mathematics: Numbers! It introduces different types of number systems that we use for counting and calculations.

You will learn about various number systems like natural numbers (whole numbers starting from 1), whole numbers (including 0 with natural numbers), integers (whole numbers and their negatives), rational numbers (numbers expressible as a fraction p/q where q ≠ 0), and irrational numbers (numbers that cannot be expressed as a fraction, like the square root of 2).

The chapter explores properties like closure, commutativity, associativity, and distributivity for different operations (addition, subtraction, multiplication, division) on these number systems.

You will revisit how to represent these numbers on the number line, which is a visual aid to understand their relative positions and comparisons.

This article contains chapter notes, important questions, exemplar solutions and exercises links for Chapter 1 - Number System, which you can download as PDFs.

There are six exercises (27 fully solved questions) in class 10th maths chapter 3 Pair of Linear Equations in Two Variables.

Access Exercise Wise NCERT Solutions for Chapter 1 Maths Class 9

Exercises under ncert solutions for class 9 maths chapter 1 number systems.

Exercise 1.1: This exercise covers basic concepts of the number system, such as natural numbers, whole numbers, integers, rational numbers, irrational numbers, etc. The questions in this exercise aim to familiarise students with these concepts and their properties.

Exercise 1.2: This exercise covers the representation of numbers in decimal form. The questions in this exercise require students to convert fractions into decimals, decimals into fractions, and perform basic operations such as addition, subtraction, multiplication, and division on decimals.

Exercise 1.3: This exercise deals with the representation of rational numbers on a number line. The questions in this exercise require students to mark the position of given rational numbers on a number line and identify the rational number represented by a given point on the number line.

Exercise 1.4: This exercise deals with the conversion of recurring decimals into fractions. The questions in this exercise require students to write recurring decimals as fractions and vice versa.

Exercise 1.5: This exercise covers the comparison of rational numbers. The questions in this exercise require students to compare given rational numbers using the concept of inequality, find rational numbers between two given rational numbers, and represent rational numbers on a number line.

NCERT Solutions Class 9 Maths Chapter 1 Number System - Free PDF Download

Exercise (1.1).

1.  Is zero a rational number? Can you write it in the form  $\dfrac{ {p}}{ {q}}$, where $ {p}$ and $ {q}$ are integers and $ {q}\ne  {0}$? Describe it.

Ans: Remember that, according to the definition of rational number,

a rational number is a number that can be expressed in the form of  $\dfrac{p}{q}$, where $p$ and $q$ are integers and  $q\ne \text{0}$.

Now, notice that zero can be represented as $\dfrac{0}{1},\dfrac{0}{2},\dfrac{0}{3},\dfrac{0}{4},\dfrac{0}{5}.....$

Also, it can be expressed as $\dfrac{0}{-1},\dfrac{0}{-2},\dfrac{0}{-3},\dfrac{0}{-4}.....$

Therefore, it is concluded from here that $0$ can be expressed in the form of $\dfrac{p}{q}$, where $p$ and $q$ are integers.

Hence, zero must be a rational number.

2. Find any six rational numbers between $ {3}$ and $ {4}$. 

Ans: It is known that there are infinitely many rational numbers between any two numbers. Since we need to find $6$ rational numbers between $3$ and $4$, so multiply and divide the numbers by $7$ (or by any number greater than $6$)

Then it gives, 

$ 3=3\times \dfrac{7}{7}=\dfrac{21}{7} $ 

$  4=4\times \dfrac{7}{7}=\dfrac{28}{7} $

Hence, $6$ rational numbers found between $3$ and $4$ are $\dfrac{22}{7},\dfrac{23}{7},\dfrac{24}{7},\dfrac{25}{7},\dfrac{26}{7},\dfrac{27}{7}$.

3. Find any five rational numbers between $\dfrac{ {3}}{ {5}}$ and $\dfrac{ {4}}{ {5}}$.

Ans: It is known that there are infinitely many rational numbers between any two numbers.

Since here we need to find five rational numbers between $\dfrac{3}{5}$ and $\dfrac{4}{5}$,  so multiply and divide by $6$ (or by any number greater than $5$).

Then it gives,

$\dfrac{3}{5}=\dfrac{3}{5}\times \dfrac{6}{6}=\dfrac{18}{30}$,

$\dfrac{4}{5}=\dfrac{4}{5}\times \dfrac{6}{6}=\dfrac{24}{30}$.

Hence, $5$ rational numbers found between $\dfrac{3}{5}$ and $\dfrac{4}{5}$ are

$\dfrac{19}{30},\dfrac{20}{30},\dfrac{21}{30},\dfrac{22}{30},\dfrac{23}{30}$.

4. State whether the following statements are true or false. Give reasons for your answers. 

(i) Every natural number is a whole number. 

Ans: Write the whole numbers and natural numbers in a separate manner.

It is known that the whole number series is $0,1,2,3,4,5.....$. and the natural number series is $1,2,3,4,5...$.

Therefore, it is concluded that all the natural numbers lie in the whole number series as represented in the diagram given below.

Thus, it is concluded that every natural number is a whole number.

Hence, the given statement is true.

(ii) Every integer is a whole number.

Ans: Write the integers and whole numbers in a separate manner.

It is known that integers are those rational numbers that can be expressed in the form of $\dfrac{p}{q}$, where $q=1$.

Now, the series of integers is like $0,\,\pm 1,\,\pm 2,\,\pm 3,\,\pm 4,\,...$.

But the whole numbers are $0,1,2,3,4,...$.

Therefore, it is seen that all the whole numbers lie within the integer numbers, but the negative integers are not included in the whole number series.

Thus, it can be concluded from here that every integer is not a whole number.

Hence, the given statement is false.

(iii) Every rational number is a whole number.

Ans: Write the rational numbers and whole numbers in a separate manner.

It is known that rational numbers are the numbers that can be expressed in the form  $\dfrac{p}{q}$, where $q\ne 0$ and the whole numbers are represented as $0,\,1,\,2,\,3,\,4,\,5,...$

Now, notice that every whole number can be expressed in the form of $\dfrac{p}{q}$

as  \[\dfrac{0}{1},\text{ }\dfrac{1}{1},\text{ }\dfrac{2}{1},\text{ }\dfrac{3}{1},\text{ }\dfrac{4}{1},\text{ }\dfrac{5}{1}\],…

Thus, every whole number is a rational number, but all the rational numbers are not whole numbers. For example,

$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},...$ are not whole numbers.

Therefore, it is concluded from here that every rational number is not a whole number.

Exercise (1.2)

1. State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number. 

Ans: Write the irrational numbers and the real numbers in a separate manner.

The irrational numbers are the numbers that cannot be represented in the form $\dfrac{p}{q},$ where $p$ and $q$ are integers and $q\ne 0.$

For example, $\sqrt{2},3\pi ,\text{ }.011011011...$ are all irrational numbers.

The real number is the collection of both rational numbers and irrational numbers.

For example, $0,\,\pm \dfrac{1}{2},\,\pm \sqrt{2}\,,\pm \pi ,...$ are all real numbers.

Thus, it is concluded that every irrational number is a real number.

(ii) Every point on the number line is of the form $\sqrt{m}$, where m is a natural number. 

Ans: Consider points on a number line to represent negative as well as positive numbers.

Observe that, positive numbers on the number line can be expressed as $\sqrt{1,}\sqrt{1.1,}\sqrt{1.2},\sqrt{1.3},\,...$, but any negative number on the number line cannot be expressed as $\sqrt{-1},\sqrt{-1.1},\sqrt{-1.2},\sqrt{-1.3},...$, because these are not real numbers.

Therefore, it is concluded from here that every number point on the number line is not of the form $\sqrt{m}$, where $m$ is a natural number.

(iii) Every real number is an irrational number. 

Real numbers are the collection of rational numbers (Ex: $\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{5},\dfrac{5}{7},$……) and the irrational numbers (Ex: $\sqrt{2},3\pi ,\text{ }.011011011...$).

Therefore, it can be concluded that every irrational number is a real number, but

every real number cannot be an irrational number.

2. Are the square roots of all positive integer numbers irrational? If not, provide an example of the square root of a number that is not an irrational number.

Ans: Square root of every positive integer does not give an integer.

For example: $\sqrt{2},\sqrt{3,}\sqrt{5},\sqrt{6},...$ are not integers, and hence these are irrational numbers. But $\sqrt{4}$ gives $\pm 2$ , these are integers and so, $\sqrt{4}$ is not an irrational number.

Therefore, it is concluded that the square root of every positive integer is not an irrational number.

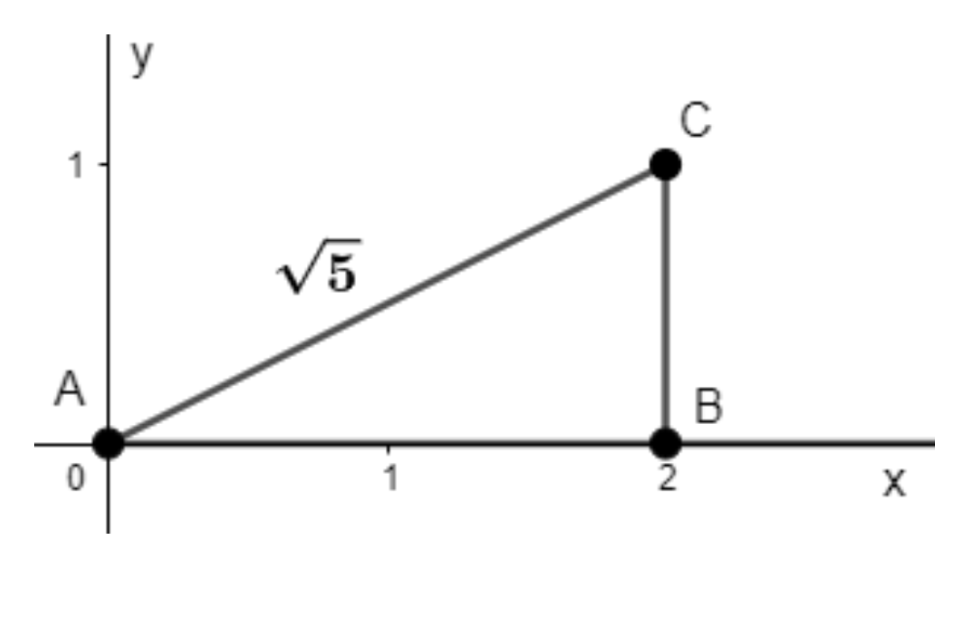
3. Represent $\sqrt{5}$ on the number line.

Ans: Follow the procedures to get $\sqrt{5}$ on the number line.

Firstly, Draw a line segment $AB$ of $2$ unit on the number line.

Secondly, draw a perpendicular line segment $BC$ at $B$ of $1$ units.

Thirdly, join the points $C$ and $A$, to form a line segment $AC$. 

Fourthly, apply the Pythagoras Theorem as 

$ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} $

$  A{{C}^{2}}={{2}^{2}}+{{1}^{2}} $

$ A{{C}^{2}}=4+1=5 $

$ AC=\sqrt{5} $

Finally, draw the arc $ACD$, to find the number $\sqrt{5}$ on the number line as given in the diagram below.

Exercise (1.3)

1. Write the following in decimal form and say what kind of decimal expansion each has:

(i) $\mathbf{\dfrac{ {36}}{ {100}}}$

Ans: Divide $36$ by $100$. 

$\,\,\,\,\,\,\,\,\,\, {0.36}$

$100 {\overline{)\;36\quad}}$

$\underline{\,\,\,\,\,\,\,\,\,-0\quad}$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,360$

$\underline{\,\,\,\,\,\,\,\,\,\,-300\quad}$

$\;\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,600$

$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,-600}$

$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\quad 0 \,\,\,\,\,}$

So, $\dfrac{36}{100}=0.36$ and it is a terminating decimal number.

(ii) $\mathbf{\dfrac{ {1}}{ {11}}}$

Ans: Divide $1$ by $11$.

${\,\,\,\,\,\,\,\,0.0909..}$

$11 \, {\overline{)\;1\quad}}$

$\underline{\,\,\,\,\,\,\,-0\quad}$

$\,\,\,\,\,\,\,\,\,\,10$

$\underline{\,\;\;\,\,-0\quad}$

$\;\;\,\,\,\,100$

$\underline{\,\,\,\,\;-99}$

$\,\,\,\,\,\, \quad 10$

$\quad\underline{\;\;-0\quad}$

$\;\;\,\,\,\,\,\,\,\,100$

$\underline{\,\,\,\,\,\,\,\,\;-99}$

$\quad\,\,\,\,\,\,\,1\quad$

It is noticed that while dividing $1$ by $11$, in the quotient $09$ is repeated.

So, $\dfrac{1}{11}=0.0909.....$ or 

$\dfrac{1}{11}=0.\overline{09}$ 

and it is a non-terminating and recurring decimal number.

(iii)  $ \mathbf{{4}\dfrac{ {1}}{ {8}}}$

Ans: $4\dfrac{1}{8}=4+\dfrac{1}{8}=\dfrac{32+1}{8}=\dfrac{33}{8}$

Divide $33$ by $8$.

$\,\,\,\,\,{4.125}$

$8 {\overline{)\;33\quad}}$

$\underline{\,\,\,\,-32\quad}$

$\,\,\,\,\,\,\,\,\,\,\,\,10$

$\underline{\;\;\,\,\,\,-8\quad}$

$\;\;\,\,\,\,\,\,\,\,\,\,\,20$

$\underline{\,\,\,\,\,\,\,\,\,-16}$

$\;\quad\quad\,\,\,\,40$

$\quad\underline{\quad\,\,-40\quad}$

$\quad\underline{\quad\,\, \,\,\,\,0\quad}$

Notice that, after dividing $33$ by $8$, the remainder is found as $0$.

So, $4\dfrac{1}{8}=4.125$ and it is a terminating decimal number.

(iv)  $\mathbf{\dfrac{ {3}}{ {13}}}$

Ans: Divide $3$ by $13$.

$\quad \,\,{0.230769}$

$13 {\overline{)\;3\quad}}$

$\underline{\quad-0\quad}$

$\quad\quad 30$

$\underline{\;\,\quad-26\quad}$

$\;\quad\quad\,\,\,40$

$\underline{\quad\quad\,\,-39\quad}$

$\;\quad\quad\quad\;10$

$\quad\underline{\quad\quad -0\quad}$

$\quad{\quad\quad \quad 100}$

$\quad\quad\underline{\quad \,\, -91\quad}$

$\quad\quad \quad \,\,\,\quad90$

$\quad\quad\underline{\quad\,\,\,\,\,-78\quad}$

$\quad\quad\quad\quad \quad 120$

$\quad \quad\underline{\quad\quad\,\,-117\quad}$

$\quad\quad\underline{\quad \quad\quad\,\, 3\quad}$

It is observed that while dividing $3$ by $13$, the remainder is found as $3$ and that is repeated after each $6$ continuous divisions.

So, $\dfrac{3}{13}=0.230769.......$ or

$\dfrac{3}{13}=0.\overline{230769}$ 

(v)   $\mathbf{\dfrac{ {2}}{ {11}}}$

Ans: Divide $2$ by $11$.

$\quad \,\,{0.1818}$

$11 {\overline{)\;2\quad}}$

$\quad\quad20$

$\underline{\quad\;-11\quad}$

$\quad\quad \;\,90$

$\underline{\quad\,\,\,\, -88\;}$

$\;\quad\quad\;20$

$\quad\underline{\quad-11\quad}$

$\quad{\quad\quad  90}$

$\quad\underline{\,\,\quad -88}$

$\quad\quad\quad\,\,2\quad$

It can be noticed that while dividing $2$ by $11$, the remainder is obtained as $2$ and then $9$, and these two numbers are repeated infinitely as remainders.

So, $\dfrac{2}{11}=0.1818.....$ or 

$\dfrac{2}{11}=0.\overline{18}$ 

(vi) $\mathbf{\dfrac{ {329}}{ {400}}}$

Ans: Divide $329$ by $400$.

$\quad \quad{0.8225}$

$400 {\overline{)\;329\quad}}$

$\underline{\quad\,\,-0\quad}$

$\quad\quad3290$

$\underline{\quad\;-3200\quad}$

$\quad\quad\quad\;900$

$\underline{\quad\quad\quad-800\;}$

$\quad\quad\quad\quad\;1000$

$\quad\underline{\quad\quad\quad-800\quad}$

$\quad{\quad\quad\quad\quad\,\,2000}$

$\quad\underline{\quad\quad\quad\quad-2000\quad}$

$\quad\underline{\quad\quad\quad\quad\,\,\,\,\,\, 0 \quad}$

It can be seen that while dividing $329$ by $400$, the remainder is obtained as $0$.

So, $\dfrac{329}{400}=0.8225$ and is a terminating decimal number.

2. You know that $\dfrac{ {1}}{ {7}} {=0} {.142857}...$. Can you predict what the decimal expansions of $\dfrac{ {2}}{ {7}} {,}\dfrac{ {3}}{ {7}} {,}\dfrac{ {4}}{ {7}} {,}\dfrac{ {5}}{ {7}} {,}\dfrac{ {6}}{ {7}}$  are, without actually doing the long division? If so, how?

$\text{[}$Hint: Study the remainders while finding the value of $\dfrac{ {1}}{ {7}}$ carefully.$\text{]}$

Ans: Note that,  $\dfrac{2}{7},\dfrac{3}{7},\dfrac{4}{7},\dfrac{5}{7}$ and $\dfrac{6}{7}$ can be rewritten as $2\times \dfrac{1}{7},\text{ 3}\times \dfrac{1}{7},\text{ 4}\times \dfrac{1}{7},\text{ 5}\times \dfrac{1}{7},$ and $6\times \dfrac{1}{7}$

Substituting the value of $\dfrac{1}{7}=0.142857$ , gives 

$2 \times \dfrac{1}{7} = 2\times 0.142857...=0.285714...$

$ 3\times \dfrac{1}{7} = 3\times .428571…= .428571...$

\[4\times \dfrac{1}{7}=4\times 0.142857...\]\[\text{=}\,\text{0}\text{.571428}...\]

$5\times \dfrac{1}{7}=5\times 0.71425...$  \[\text{=}\,\text{0}\text{.714285}...\]

$6\times \dfrac{1}{7}=6\times 0.142857...$\[\text{=}\,\text{0}\text{.857142}...\]

So, the values of $\dfrac{2}{7},\text{ }\dfrac{3}{7},\text{ }\dfrac{4}{7},\text{ }\dfrac{5}{7}$ and $\dfrac{6}{7}$ obtained without performing long division are

\[\dfrac{2}{7}=0.\overline{285714}\]

$\dfrac{3}{7}=0.\overline{428571}$

$\dfrac{4}{7}=0.\overline{571428}$

\[\dfrac{5}{7}=0.\overline{714285}\]

$\dfrac{6}{7}=0.\overline{857142}$

3. Express the following in the form \[\dfrac{ {p}}{ {q}}\], where $ {p}$ and $ {q}$ are integers and $ {q}\ne  {0}$.

(i) $\mathbf{ {0} {.}\overline{ {6}}}$

Ans: Let $x=0.\overline{6}$  

 $\Rightarrow x=0.6666$                                                   ….… (1)

 Multiplying both sides of the equation (1) by $10$, gives

$10x=0.6666\times 10$

$10x=6.6666$…..                 …… (2)

Subtracting the equation $\left( 1 \right)$ from $\left( 2 \right)$, gives

$ 10x=6.6666..... $

$ \underline{-x=0.6666.....} $

$  9x=6 $ 

$  9x=6 $

$  x=\dfrac{6}{9}=\dfrac{2}{3} $ 

So, the decimal number becomes

$0.\overline{6}=\dfrac{2}{3}$  and it is in the required  $\dfrac{p}{q}$ form.

(ii) $\mathbf{ {0} {.}\overline{ {47}}}$

Ans: Let  $x=0.\overline{47}$

$\text{   }\Rightarrow x=0.47777.....$                                             ……(a)

Multiplying both sides of the equation (a) by $10$, gives

$10x=4.7777.....$         ……(b)

Subtracting the equation $\left( a \right)$ from $\left( b \right)$, gives

$ 10x=4.7777..... $

$  \underline{-x=0.4777.....} $

$  9x=4.3 $

$x=\dfrac{4.3}{9}\times \dfrac{10}{10} $ 

$ \Rightarrow x=\dfrac{43}{90} $

So, the decimal number becomes 

$0.\overline{47}=\dfrac{43}{90}$  and it is in the required $\dfrac{p}{q}$ form.

(iii) $ \mathbf{{0} {.}\overline{ {001}}}$

Ans: Let $x=0.\overline{001} $           …… (1)

Since the number of recurring decimal number is $3$, so multiplying both sides of the equation (1) by $1000$, gives

$1000\times x=1000\times 0.001001.....$ …… (2)

Subtracting the equation (1) from (2) gives

$ 1000x=1.001001..... $

$  \underline{\text{    }-x=0.001001.....} $

$  999x=1 $

$\Rightarrow x=\dfrac{1}{999}$

Hence, the decimal number becomes 

$0.\overline{001}=\dfrac{1}{999}$ and it is in the $\dfrac{p}{q}$ form.

4. Express $ {0} {.99999}.....$ in the form of $\dfrac{ {p}}{ {q}}$ . Are you surprised by your answer? With your teacher and classmates, discuss why the answer makes sense.

Let $x=0.99999.....$                                                             ....... (a)

Multiplying by $10$ both sides of the equation (a), gives

$10x=9.9999.....$                                                             …… (b)

Now, subtracting the equation (a) from (b), gives

$ 10x=9.99999..... $

$  \underline{\,-x=0.99999.....} $

$  9x=9 $ 

$\Rightarrow x=\dfrac{9}{9}$

$\Rightarrow x=1$.

$0.99999...=\dfrac{1}{1}$ which is in the $\dfrac{p}{q}$ form.

Yes, for a moment we are amazed by our answer, but when we observe that $0.9999.........$ is extending infinitely, then the answer makes sense.

Therefore, there is no difference between $1$ and $0.9999.........$ and hence these two numbers are equal.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\dfrac{ {1}}{ {17}}$ ? Perform the division to check your answer.

Ans: Here the number of digits in the recurring block of $\dfrac{1}{17}$ is to be determined. So, let us calculate the long division to obtain the recurring block of $\dfrac{1}{17}$. Dividing $1$ by $17$ gives

$\quad\quad {0.0588235294117646}$

$17{\overline{)\quad1\quad\quad\quad\quad\quad\quad\quad\quad}}$

$\underline{\quad\,\,\,\,-0\quad}\qquad\qquad\qquad$

$\quad \quad \,\,\,10\qquad\qquad\quad\quad$

$\underline{\quad \quad -0\quad}\qquad\qquad\quad$

$\quad \quad \,\,\,\,\,\;100\qquad\qquad\qquad$

$\underline{\quad \quad \,\,-85\;}\qquad\qquad\quad$

$\quad\qquad\,\,\;150\qquad\qquad\quad$

$\quad\underline{\qquad-136\;}\qquad\qquad\quad$

$\quad{\quad\quad\quad 140}\qquad\qquad\;\;$

$\quad\underline{\qquad-136\quad}\qquad\quad$

${\quad \qquad \,\,\quad 40 \quad}\quad$

$\underline{\qquad \,\,\,\quad -34\;\;}\quad$

$\;\qquad \qquad\,\,60$

$\underline{\qquad \qquad-51}$

$\quad\quad \qquad \quad 90$

$\quad\;\;\underline{\quad \qquad-85}$

$\qquad\quad\;\quad\,\,\,\, 50$

$\quad\quad\;\;\underline{\,\,\quad\,\, -34}$

$\quad\quad\qquad \quad 160$

$\qquad\quad\;\underline{\quad-153}$

$\qquad\qquad\quad\;70$

$\qquad\quad\quad\;\;\underline{-68}$

$\quad\,\,\qquad\qquad 20$

$\qquad\qquad\quad\underline{-17}$

$\qquad\qquad\quad\quad\; 130$

$\qquad\qquad\quad\;\;\underline{-119}$

$\qquad\qquad\qquad\quad 110$

$\qquad\qquad\qquad\;\;\underline{-102}$

$\qquad\qquad\qquad\quad\quad\quad 80$

$\qquad\qquad\qquad\qquad\;\underline{-68}$

$\qquad\qquad\qquad\quad\quad\quad\; 120$

$\qquad\qquad\qquad\qquad\;\;\underline{-119}$

$\qquad\qquad\qquad\quad\quad\quad\; 1$

Thus, it is noticed that while dividing $1$ by $17$, we found $16$ number of digits in the

repeating block of decimal expansion that will continue to be $1$ after going through $16$ continuous divisions.

Hence, it is concluded that $\dfrac{1}{17}=0.0588235294117647.....$ or 

 $\dfrac{1}{17}=0.\overline{0588235294117647}$ and it is a recurring and non-terminating decimal number.

6. Look at several examples of rational numbers in the form $\dfrac{ {p}}{ {q}}\left(  {q}\ne  {0} \right)$, where $ {p}$ and $ {q}$ are integers with no common factors other than $ {1}$ and having terminating decimal representations (expansions). Can you guess what property $ {q}$ must satisfy?

Ans: Let us consider the examples of such rational numbers $\dfrac{5}{2},\dfrac{5}{4},\dfrac{2}{5},\dfrac{2}{10},\dfrac{5}{16}$ of the form $\dfrac{p}{q}$ which have terminating decimal representations.

$ \dfrac{5}{2}=2.5 $

$ \dfrac{5}{4}=1.25 $ 

$ \dfrac{2}{5}=0.4 $

$ \dfrac{2}{10}=0.2 $

$ \dfrac{5}{16}=0.3125 $

In each of the above examples, it can be noticed that the denominators of the rational numbers have powers of $2,5$ or both.

So, $q$ must satisfy the form either ${{2}^{m}}$, or ${{5}^{n}}$, or  both ${{2}^{m}}\times {{5}^{n}}$ (where $m=0,1,2,3.....$ and $n=0,1,2,3.....$) in the form of $\dfrac{p}{q}$.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Ans: All the irrational numbers are non-terminating and non-recurring, because irrational numbers do not have any representations of the form of $\dfrac{p}{q}$ $\left( q\ne 0 \right)$, where $p$ and $q$are integers. For example: 

$\sqrt{2}=1.41421.....$,

$\sqrt{3}=1.73205...$

$\sqrt{7}=2.645751....$

are the numbers whose decimal representations are non-terminating and non-recurring.

8. Find any three irrational numbers between the rational numbers $\dfrac{ {5}}{ {7}}$ and $\dfrac{ {9}}{ {11}}$.

Ans: Converting  $\dfrac{5}{7}$and $\dfrac{9}{11}$ into the decimal form gives

$\dfrac{5}{7}=0.714285.....$ and 

$\dfrac{9}{11}=0.818181.....$

Therefore, $3$ irrational numbers that are contained between $0.714285......$ and $0.818181.....$

$ 0.73073007300073...... $ 

$  0.74074007400074...... $ 

$ 0.76076007600076...... $

Hence, three irrational numbers between the rational numbers $\dfrac{5}{7}$ and $\dfrac{9}{11}$ are

9. Classify the following numbers as rational or irrational:

(i) $\mathbf{\sqrt{ {23}}}$

Ans: The following diagram reminds us of the distinctions among the types of rational and irrational numbers.

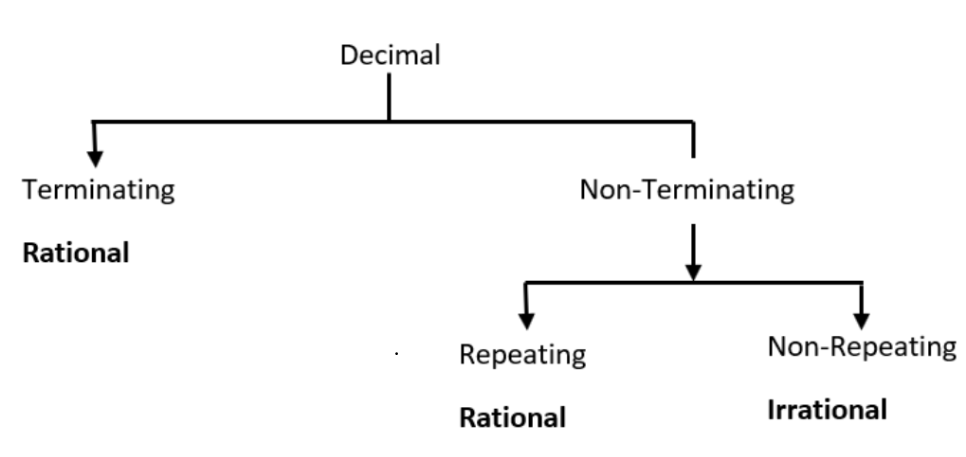
After evaluating the square root gives

$\sqrt{23}=4.795831.....$ , which is an irrational number.

(ii) $\mathbf{\sqrt{ {225}}}$

Ans: After evaluating the square root gives

$\sqrt{225}=15$, which is a rational number.

That is, $\sqrt{225}$ is a rational number.

(iii) $ \mathbf{{0} {.3796}}$

Ans: The given number is $0.3796$. It is terminating decimal. 

So, $0.3796$ is a rational number.

(iv) $ \mathbf{{7} {.478478}}$

Ans: The given number is \[7.478478\ldots .\] 

It is a non-terminating and recurring decimal that can be written in the $\dfrac{p}{q}$ form.

Let      $x=7.478478\ldots .$                                   ……(a)

Multiplying the equation (a) both sides by $100$ gives

$\Rightarrow 1000x=7478.478478.....$                                               ……(b)

Subtracting the equation (a) from (b), gives

$ 1000x=7478.478478.... $

$  \underline{\text{    }-x=\text{     }7.478478\ldots .} $

$ 999x=7471 $

$  \text{      }x=\dfrac{7471}{999} $

Therefore, $7.478478.....=\dfrac{7471}{999}$, which is in the form of $\dfrac{p}{q}$

So, $7.478478...$ is a rational number.

(v) $ \mathbf{{1} {.101001000100001}.....}$

Ans: The given number is \[1.101001000100001....\]

It can be clearly seen that the number \[1.101001000100001....\] is a non-terminating and non-recurring decimal and it is known that non-terminating non-recurring decimals cannot be written in the form of $\dfrac{p}{q}$.

Hence, the number \[1.101001000100001....\] is an irrational number.

Exercise (1.4)

1.  Classify the following numbers as rational or irrational:

(i) $ \mathbf{{2-}\sqrt{ {5}}}$

Ans: The given number is $2-\sqrt{5}$.

Here, $\sqrt{5}=2.236.....$ and it is a non-repeating and non-terminating irrational number.

Therefore, substituting the value of $\sqrt{5}$ gives

$2-\sqrt{5}=2-2.236.....$

$=-0.236.....$, which is an irrational number.

So, $2-\sqrt{5}$ is an irrational number.

(ii) $\mathbf{\left(  {3+}\sqrt{ {23}} \right) {-}\left( \sqrt{ {23}} \right)}$

Ans: The given number is $\left( 3+\sqrt{23} \right)-\left( \sqrt{23} \right)$.

The number can be written as

$\left( 3+\sqrt{23} \right)-\sqrt{23}=3+\sqrt{23}-\sqrt{23} $ 

$  =3 $

$=\dfrac{3}{1}$, which is in the $\dfrac{p}{q}$ form and so, it is a rational number.

Hence, the number $\left( 3+\sqrt{23} \right)-\sqrt{23}$ is a rational number.

(iii) $\mathbf{\dfrac{ {2}\sqrt{ {7}}}{ {7}\sqrt{ {7}}}}$

Ans: The given number is $\dfrac{2\sqrt{7}}{7\sqrt{7}}$.

$\dfrac{2\sqrt{7}}{7\sqrt{7}}=\dfrac{2}{7}$, which is in the $\dfrac{p}{q}$  form and so, it is a rational number.

Hence, the number  $\dfrac{2\sqrt{7}}{7\sqrt{7}}$ is a rational number.

(iv) $\mathbf{\dfrac{ {1}}{\sqrt{ {2}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{2}}$.

It is known that, $\sqrt{2}=1.414.....$ and it is a non-repeating and non-terminating irrational number.

Hence, the number $\dfrac{1}{\sqrt{2}}$ is an irrational number.

(v) $ \mathbf{{2\pi }}$

Ans: The given number is $2\pi $.

It is known that, $\pi =3.1415$ and it is an irrational number.

Now remember that, Rational $\times $ Irrational = Irrational.

Hence, $2\pi $ is also an irrational number.

2. Simplify each of the of the following expressions:

(i) $\mathbf{\left(  {3+}\sqrt{ {3}} \right)\left(  {2+}\sqrt{ {2}} \right)}$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)$.

By calculating the multiplication, it can be written as

$\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)=3\left( 2+\sqrt{2} \right)+\sqrt{3}\left( 2+\sqrt{2} \right)$.

\[= 6 + 4 \sqrt{2} + 2 \sqrt{3}+ \sqrt{6}\]

(ii) $\mathbf{\left(  {3+}\sqrt{ {3}} \right)\left(  {3-}\sqrt{ {3}} \right)}$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)$.

By applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be written as

$\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)={{3}^{2}}-{{\left( \sqrt{3} \right)}^{2}}=9-3=6$.

(iii)  $\mathbf{{{\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)}^{ {2}}}}$

Ans: The given number is ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$.

Applying the formula ${{\left( a+b \right)}^{2}}={{a}^{2+}}2ab+{{b}^{2}}$, the number can be written as

${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+2\sqrt{5}\sqrt{2}+{{\left( \sqrt{2} \right)}^{2}}$

 $=5+2\sqrt{10}+2$

 $=7+2\sqrt{10}$.

(iv)  $\mathbf{\left( \sqrt{ {5}}-\sqrt{ {2}} \right)\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)}$

Ans: The given number is $\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)$.

Applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be expressed as

$\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)={{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}$

$ =3. $ 

3. Recall that, $ {\pi }$ is defined as the ratio of the circumference (say $ {c}$) of a circle to its diameter (say $ {d}$). That is, $ {\pi =}\dfrac{ {c}}{ {d}}$ .This seems to contradict the fact that $ {\pi }$ is irrational. How will you resolve this contradiction?

Ans: It is known that, $\pi =\dfrac{22}{7}$, which is a rational number. But, note that this value of $\pi $ is an approximation.

On dividing $22$ by $7$, the quotient $3.14...$ is a non-recurring and non-terminating number. Therefore, it is an irrational number.

In order of increasing accuracy, approximate fractions are

$\dfrac{22}{7}$, $\dfrac{333}{106}$, $\dfrac{355}{113}$, $\dfrac{52163}{16604}$, $\dfrac{103993}{33102}$, and \[\dfrac{245850922}{78256779}\].

Each of the above quotients has the value $3.14...$, which is a non-recurring and non-terminating number.

Thus, $\pi $ is irrational.

So, either circumference $\left( c \right)$ or diameter $\left( d \right)$ or both should be irrational numbers.

Hence, it is concluded that there is no contradiction regarding the value of $\pi $ and it is made out that the value of $\pi $ is irrational.

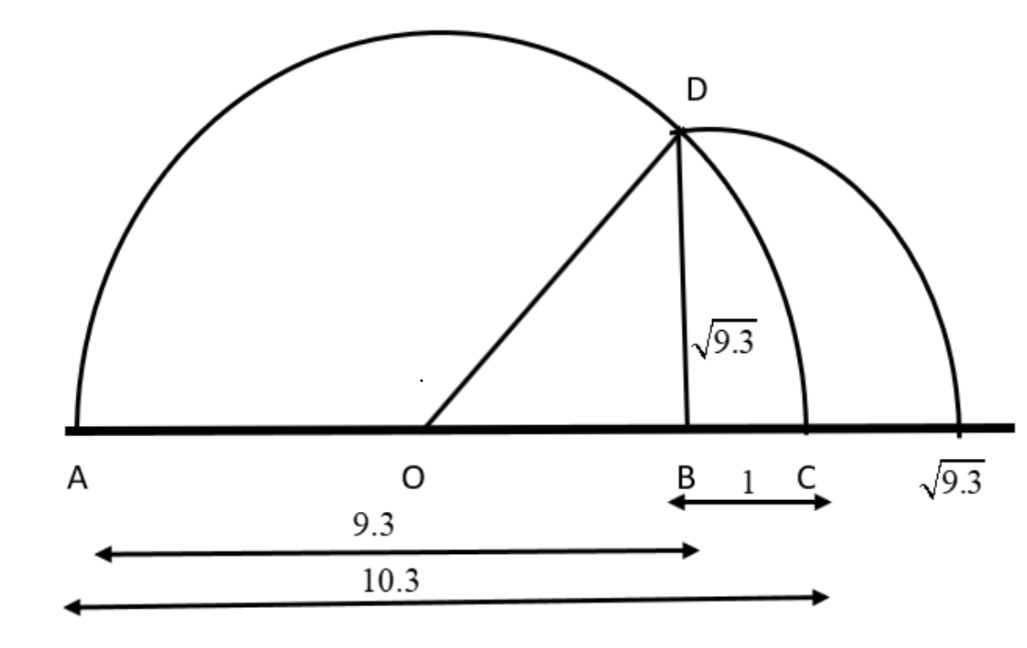
4. Represent $\sqrt{ {9} {.3}}$ on the number line.

Ans: Follow the procedure given below to represent the number $\sqrt{9.3}$.

First, mark the distance $9.3$ units from a fixed-point $A$ on the number line to get a point $B$. Then $AB=9.3$ units.

Secondly, from the point $B$ mark a distance of $1$ unit and denote the ending point as $C$.

Thirdly, locate the midpoint of $AC$ and denote it as $O$.

Fourthly, draw a semi-circle to the centre $O$ with the radius $OC=5.15$ units. Then 

$ AC=AB+BC $ 

$  =9.3+1 $ 

$  =10.3 $

So, $OC=\dfrac{AC}{2}=\dfrac{10.3}{2}=5.15$.

Finally, draw a perpendicular line at $B$ and draw an arc to the centre $B$ and then let it meet at the semicircle $AC$ at $D$ as given in the diagram below.

5. Rationalize the denominators of the following:

(i) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}}$.

Multiplying and dividing by $\sqrt{7}$ to the number gives

$\dfrac{1}{\sqrt{7}}\times \dfrac{\sqrt{7}}{\sqrt{7}}=\dfrac{\sqrt{7}}{7}$.

(ii) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}} {-}\sqrt{ {6}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-\sqrt{6}}$.

Multiplying and dividing by $\sqrt{7}+\sqrt{6}$ to the number gives

$\dfrac{1}{\sqrt{7}-\sqrt{6}}\times \dfrac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{\left( \sqrt{7}-\sqrt{6} \right)\left( \sqrt{7}+\sqrt{6} \right)}$

Now, applying the formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$ \dfrac{1}{\sqrt{7}-\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( \sqrt{6} \right)}^{2}}} $ 

$ =\dfrac{\sqrt{7}+\sqrt{6}}{7-6} $ 

$  =\dfrac{\sqrt{7}+\sqrt{6}}{1}. $

(iii) $\mathbf{\dfrac{ {1}}{\sqrt{ {5}} {+}\sqrt{ {2}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{5}+\sqrt{2}}$.

Multiplying and dividing by $\sqrt{5}-\sqrt{2}$ to the number gives

$\dfrac{1}{\sqrt{5}+\sqrt{2}}\times \dfrac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)}$

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$  to the denominator gives

$ \dfrac{1}{\sqrt{5}+\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}} $ 

$ =\dfrac{\sqrt{5}-\sqrt{2}}{5-2} $

$ =\dfrac{\sqrt{5}-\sqrt{2}}{3}. $ 

(iv) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}} {-2}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-2}$.

Multiplying and dividing by $\sqrt{7}+2$ to the number gives

$\dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{\left( \sqrt{7}-2 \right)\left( \sqrt{7}+2 \right)}\\$.

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$ \dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( 2 \right)}^{2}}} $

$ =\dfrac{\sqrt{7}+2}{7-4} $ 

$  =\dfrac{\sqrt{7}+2}{3}. $

Exercise (1.5)

1. Compute the value of each of the following expressions:

(i) $\mathbf{ {6}{{ {4}}^{\dfrac{ {1}}{ {2}}}}}$

Ans: The given number is \[{{64}^{\dfrac{1}{2}}}\].

By the laws of indices,

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$, where$a>0$.

$ {{64}^{\dfrac{1}{2}}}=\sqrt[2]{64} $

$  =\sqrt[2]{8\times \text{8}} $

$  =8. $

Hence, the value of ${{64}^{\dfrac{1}{2}}}$ is $8$.

(ii) $ \mathbf{{3}{{ {2}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given number is ${{32}^{\dfrac{1}{5}}}$.

${{a}^{\dfrac{m}{n}}}=\sqrt[m]{{{a}^{m}}}$, where $a>0$

$ {{32}^{\dfrac{1}{5}}}=\sqrt[5]{32}$

$ =\sqrt[5]{2\times 2\times 2\times 2\times 2} $ 

$ =\sqrt[5]{{{2}^{5}}} $

Alternative Method:

By the law of indices ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$, then it gives

$ {{32}^{\dfrac{1}{5}}}={{(2\times 2\times 2\times 2\times 2)}^{\dfrac{1}{5}}}$ 

$ ={{\left( {{2}^{5}} \right)}^{\dfrac{1}{5}}} $

$ ={{2}^{\dfrac{5}{5}}} $

Hence, the value of the expression ${{32}^{\dfrac{1}{5}}}$ is $2$.

(iii) $\mathbf{{12}{{ {5}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given number is ${{125}^{\dfrac{1}{3}}}$.

By the laws of indices

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where$a>0$.

$ {{125}^{\dfrac{1}{3}}}=\sqrt[3]{125} $

$  =\sqrt[3]{5\times 5\times 5} $

$  =5. $

Hence, the value of the expression ${{125}^{\dfrac{1}{3}}}$ is $5$.

2. Compute the value of each of the following expressions:

(i) $\mathbf{{{ {9}}^{\dfrac{ {3}}{ {2}}}}}$

Ans: The given number is ${{9}^{\dfrac{3}{2}}}$.

 ${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where $a>0$.

$ {{9}^{\dfrac{3}{2}}}=\sqrt[2]{{{\left( 9 \right)}^{3}}} $

$  =\sqrt[2]{9\times 9\times 9} $

$ =\sqrt[2]{3\times 3\times 3\times 3\times 3\times 3} $

$=3\times 3\times 3 $

By the laws of indices, ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$, then it gives

$ {{9}^{\dfrac{3}{2}}}={{\left( 3\times 3 \right)}^{\dfrac{3}{2}}}$

$  ={{\left( {{3}^{2}} \right)}^{\dfrac{3}{2}}} $

$  ={{3}^{2\times \dfrac{3}{2}}} $

$ ={{3}^{3}} $

${{9}^{\dfrac{3}{2}}}=27.$

Hence, the value of the expression ${{9}^{\dfrac{3}{2}}}$ is $27$.

(ii) $\mathbf{{3}{{ {2}}^{\dfrac{ {2}}{ {5}}}}}$

Ans: We know that ${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where $a>0$.

We conclude that ${{32}^{\dfrac{2}{5}}}$ can also be written as

$ \sqrt[5]{{{\left( 32 \right)}^{2}}}=\sqrt[5]{\left( 2\times 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2\times 2 \right)} $ 

$  =2\times 2 $

$ =4 $ 

Therefore, the value of ${{32}^{\dfrac{2}{5}}}$ is $4$.

(iii) $\mathbf{{1}{{ {6}}^{\dfrac{ {3}}{ {4}}}}}$

Ans: The given number is ${{16}^{\dfrac{3}{4}}}$.

By the laws of indices, 

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$, where $a>0$.

$ {{16}^{\dfrac{3}{4}}}=\sqrt[4]{{{\left( 16 \right)}^{3}}} $

$  =\sqrt[4]{\left( 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2 \right)} $

$  =2\times 2\times 2 $

Hence, the value of the expression ${{16}^{\dfrac{3}{4}}}$ is $8$.

${{({{a}^{m}})}^{n}}={{a}^{mn}}$, where $a>0$.

$ {{16}^{\dfrac{3}{4}}}={{(4\times 4)}^{\dfrac{3}{4}}} $

$  ={{({{4}^{2}})}^{\dfrac{3}{4}}} $ 

$ ={{(4)}^{2\times \dfrac{3}{4}}} $

$ ={{({{2}^{2}})}^{2\times \dfrac{3}{4}}} $ 

$ ={{2}^{2\times 2\times \dfrac{3}{4}}} $

$ ={{2}^{3}} $

Hence, the value of the expression is ${{16}^{\dfrac{3}{4}}}=8$.

(iv) $\mathbf{{12}{{ {5}}^{ {-}\dfrac{ {1}}{ {3}}}}}$

Ans: The given number is ${{125}^{-\dfrac{1}{3}}}$.

By the laws of indices, it is known that 

${{a}^{-n}}=\dfrac{1}{{{a}^{^{n}}}}$, where $a>0$.

Therefore, 

$ {{125}^{-\dfrac{1}{3}}}=\dfrac{1}{{{125}^{\dfrac{1}{3}}}} $

$  ={{\left( \dfrac{1}{125} \right)}^{\dfrac{1}{3}}} $

$ =\sqrt[3]{\left( \dfrac{1}{125} \right)} $

$ =\sqrt[3]{\left( \dfrac{1}{5}\times \dfrac{1}{5}\times \dfrac{1}{5} \right)} $

$ =\dfrac{1}{5}. $

Hence, the value of the expression ${{125}^{-\dfrac{1}{3}}}$ is  $\dfrac{1}{5}$.

3. Simplify and evaluate each of the expressions:

(i)$\mathbf{{{ {2}}^{\dfrac{ {2}}{ {3}}}} {.}{{ {2}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given expression is ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}$.

By the laws of indices, it is known that

${{a}^{m}}\cdot {{a}^{n}}={{a}^{m+n}}$, where $a>0$.

 ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}={{(2)}^{\dfrac{2}{3}+\dfrac{1}{5}}}$

 $ ={{(2)}^{\dfrac{10+3}{15}}} $

 $ ={{2}^{\dfrac{13}{15}}}. $

Hence, the value of the expression ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}$ is ${{2}^{\dfrac{13}{15}}}$.

(ii) ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$

Ans: The given expression is  ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$.

It is known by the laws of indices that,

 ${{({{a}^{m}})}^{n}}={{a}^{mn}}$, where $a>0$.

 ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}} =\left ( \dfrac{1}{3^{21}} \right )$

Hence, the value of the expression  ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$ is  $\left ( \dfrac{1}{3^{21}} \right )$

(iii) $\dfrac{ {1}{{ {1}}^{\dfrac{ {1}}{ {2}}}}}{ {1}{{ {1}}^{\dfrac{ {1}}{ {4}}}}}$

Ans: The given number is $\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}$.

It is known by the Laws of Indices that

 $\dfrac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}}$, where $a>0$.

$\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}={{11}^{\dfrac{1}{2}-\dfrac{1}{4}}} $

$ ={{11}^{\dfrac{2-1}{4}}} $ 

$  ={{11}^{\dfrac{1}{4}}}. $

Hence, the value of the expression $\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}$ is  ${{11}^{\dfrac{1}{4}}}$.

(iv) $\mathbf{{{ {7}}^{\dfrac{ {1}}{ {2}}}} {.}{{ {8}}^{\dfrac{ {1}}{ {2}}}}}$

Ans: The given expression is ${{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}$.

${{a}^{m}}\cdot {{b}^{m}}={{(a\cdot b)}^{m}}$, where $a>0$.

$ {{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}={{(7\times 8)}^{\dfrac{1}{2}}} $  $={{(56)}^{\dfrac{1}{2}}}. $

Hence, the value of the expression ${{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}$ is ${{(56)}^{\dfrac{1}{2}}}$.

Class 9 Maths Chapter 1 Solutions - Free PDF Download

The NCERT Solutions for Class 9 Maths Chapter 1, "Number Systems," serve as the first chapter of the Class 9 Maths curriculum. This chapter provides an in-depth discussion on Number Systems and their applications, starting with an introduction to whole numbers, integers, and rational numbers.

The chapter begins with an overview of Number Systems in section 1.1, followed by two crucial topics in sections 1.2 and 1.3:

Irrational Numbers : These are numbers that cannot be expressed in the form p/q.

Real Numbers and their Decimal Expansions : This section examines the decimal expansions of real numbers to differentiate between rational and irrational numbers.

Further, the chapter covers:

Representing Real Numbers on the Number Line: Solutions for two problems in Exercise 1.4 are provided.

Operations on Real Numbers: This section explores operations such as addition, subtraction, multiplication, and division involving irrational numbers.

Laws of Exponents for Real Numbers: These laws are used to solve various questions.

NCERT Solutions for Class 9 Maths Chapter 1 All Exercise

The class 9 maths chapter 1 PDF solutions by Vedantu provide a detailed and clear explanation of the concepts in the chapter. This chapter covers important topics like rational and irrational numbers, real numbers, and their decimal expansions. Understanding these foundational concepts is crucial for success in higher-level maths. When studying, focus on grasping the properties of different types of numbers and practising their operations. The solutions by Vedantu simplify these concepts with step-by-step explanations, making them easier to understand. In previous year question papers, typically 3 to 5 questions from this chapter are asked. These questions often test your understanding of number classification, representation of numbers on the number line, and converting between different forms of numbers. Therefore, practice is key to mastering this chapter and performing well in exams.

Other Related Links for CBSE Class 9 Maths Chapter 1

Chapter-specific ncert solutions for class 9 maths.

Given below are the chapter-wise NCERT Solutions for Class 9 Maths . Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Study Materials for CBSE Class 9 Maths

Faqs on ncert solutions for class 9 maths chapter 1 number systems.

1. What all Comes Under the Purview of NCERT Maths Class 9 Chapter 1 Number Systems?

The subjects covered in NCERT mathematics class 9 chapter 1 Number Systems include a brief introduction to number systems using number lines, defining rational and irrational numbers using fractions, defining real numbers and declaring their decimal expansions. The chapter then returns to the number line to teach pupils how to express real numbers on it. In addition, the chapter teaches pupils how to add, subtract, multiply, and divide real numbers, or how to perform operations on real numbers. The rules of exponents for real numbers are a part of operations and are the final topic in class 9 mathematics chapter 1.

2. What are the Weightage Marks for Mathematics in Class 9?

The total mathematics paper in class 9 is 100 marks, like any other subject. Out of these 100 marks, 20 marks goes from internal assessments (pen and paper tests, multiple assessments, portfolios/project work and lab practicals for 5 marks each), and the remaining 80 marks are from the written test at the end of the school year. Out of these 80 marks, the chapter Number Systems comes for 8 marks, Algebra for 17 marks,  Coordinate Geometry for 4 marks, Geometry for 28 marks, Mensuration for 13 marks, and Statistics and Probability for 10 marks. All of these chapters’ respective marks total up to a cumulative 80 marks for the written paper.

3. How many sums are there in the NCERT Class 9 Chapter 1 Number System?

There are six exercises in the NCERT Class 9 Chapter 1 Number System. In the first exercise, Ex-1.1, there are 4 sums and in the second exercise, Ex-1.2, there are 3 sums. These first two exercises deal with the basic concepts of the number system, such as identifying the features of a rational number or an irrational number and locating them on the number line. In the third exercise, Ex-1.3, there are 9 sums, and most of them have sub-questions. The fourth exercise, Ex-1.4, comprises 2 sums, that deal with successive magnification for locating a decimal number on the number line. The fifth exercise, Ex-1.5, consists of 5 sums, on the concept of rationalization. The sixth exercise, Ex-1.6, consists of 3 sums, that have sub-questions. The sums in this exercise will require you to find the various roots of numbers.

4. Why should we download NCERT Solutions for Class 9 Maths Chapter 1?

Students should download NCERT Solutions for Class 9 Maths Chapter 1 from Vedantu (vedantu.com) to understand and learn the concepts of the Number System easily. These solutions are available free of cost on Vedantu (vedantu.com). Students must have a solid base of all concepts of Class 9 Maths if they want to score well in their exams. They can download the NCERT Solutions and other study materials such as important questions and revision notes for all subjects of Class 9. You can download these from Vedantu mobile app also.

5. Why are Class 9 Maths NCERT Solutions Chapter 1 important?

Some students find it difficult to study and score good marks in their Maths exam. They get nervous while preparing for it and goof up in their exams. However, if they utilise the best resources for studying, they can do well. This is why the Class 9 Maths NCERT Solutions Chapter 1 is important. The answers to all the questions from the back of each chapter are provided for the reference of students. 

6. Give an overview of concepts present in NCERT Solutions for Class 9 Maths Chapter 1?

The concepts in the NCERT Solutions for Class 9 Maths Chapter 1 include the introduction of number systems, rational and irrational numbers using fractions, defining real numbers, decimal expansions of real numbers, number line, representing real numbers on a number line, addition, subtraction, multiplication and division of real numbers and laws of exponents for real numbers. Chapter 1 of Class 9 Maths has a weightage of 8 marks in the final exam. 

7. Do I Need to Practice all Questions Provided in NCERT Solutions Class 9 Maths Number Systems?

Yes. Students should practice all the questions provided in the NCERT Solutions of the Number Systems chapter of Class 9 Maths, as they have been created with precision and accuracy, by expert faculty, for the students. Students can access them for free and also download them for offline use to reduce their screen time. The solutions are beneficial not only for exams but also for school homework.

8. Where can I get the NCERT Solutions for Class 9 Maths Chapter 1?

Students can download the NCERT Solutions for Class 9 Maths Chapter 1 from NCERT Solutions for Class 9 Maths Chapter 1. These are available free of cost on Vedantu (vedantu.com). These can be downloaded from the Vedantu app as well. The answers to all the questions from the 6 exercises of Chapter 1 Number Systems are provided in the NCERT Solutions. Students would also learn how to solve one question with different techniques if available. This will help them learn how to structure their answers in their Class 9 Maths exam.