- Notifications 0

- Add Friend ($5)

As a registered member you can:
- View all solutions for free
- Request more in-depth explanations for free
- Ask our tutors any math-related question for free
- Email your homework to your parent or tutor for free
- Grade 5 Eureka - Answer Keys Module 2
Thank you for doing your homework!

Submit Your Question
- Texas Go Math
- Big Ideas Math
- enVision Math
- EngageNY Math
- McGraw Hill My Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy

Texas Go Math Grade 5 Lesson 5.2 Answer Key Subtraction with Unequal Denominators
Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 5.2 Answer Key Subtraction with Unequal Denominators.
Investigate
Mario fills a hummingbird feeder with \(\frac{3}{4}\) cup of sugar water on Friday. On Monday, Mario sees that \(\frac{1}{8}\) cup of sugar water is left. How much sugar water did the hummingbirds drink?
Materials: fraction strips; MathBoard

C. Record the difference, \(\frac{3}{4}\) – \(\frac{1}{8}\) = ___________
So, the hummingbirds drank _________ cup of sugar water. Answer:
C. Record the difference, \(\frac{3}{4}\) – \(\frac{1}{8}\) = \(\frac{6}{8}\) – \(\frac{1}{8}\) = \(\frac{5}{8}\)
So, the hummingbirds drank \(\frac{5}{8}\) cup of sugar water.
Math Talk Mathematical Processes

Draw Conclusions

Lesson 5.2 Answer Key 5th Grade Go Math Question 2. H.O.T. Explain whether you could have used fraction strips with any other denominator to find the difference. If so, what is the denominator? Answer: Unequal denominator Explanation: used fraction strips with any other denominator to find the difference. If so, that is called unequal denominator
Make Connections
Sometimes you can use different sets of same-denominator fraction strips to find the difference. All of the answers will be correct.
Solve. \(\frac{2}{3}\) – \(\frac{1}{6}\)

C. Find other fraction strips, all with the same denominator, that fit exactly under the difference \(\frac{2}{3}\) – \(\frac{1}{6}\). Draw the fraction strips you used. \(\frac{2}{3}\) – \(\frac{1}{6}\) = ____________
While each answer appears different, all of the answers can be simplified to _________. Answer:

While each answer appears different, all of the answers can be simplified to equal denominators
Which other fraction strips with the same denominator could fit exactly in the difference of \(\frac{2}{3}\) – \(\frac{1}{6}\)? Answer: \(\frac{3}{6}\) Explanation: fraction strips with the same denominator could fit exactly in the difference of \(\frac{2}{3}\) – \(\frac{1}{6}\) is \(\frac{3}{6}\)
Share and Show
Use fraction strips to find the difference. Write your answer in the simplest form.
Use fraction strips to find the difference. Write your answer in simplest form.
Question 3. \(\frac{3}{4}\) – \(\frac{1}{3}\) = _____________ Answer: \(\frac{3}{4}\) – \(\frac{1}{3}\) =\(\frac{9}{12}\) – \(\frac{4}{12}\) = \(\frac{5}{12}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 4. \(\frac{5}{6}\) – \(\frac{1}{2}\) = ______________ Answer: \(\frac{5}{6}\) – \(\frac{1}{2}\) = \(\frac{5}{6}\) – \(\frac{3}{6}\)= \(\frac{2}{6}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 5. \(\frac{3}{4}\) – \(\frac{7}{12}\) = ______________ Answer: \(\frac{3}{4}\) – \(\frac{7}{12}\) = \(\frac{9}{12}\) – \(\frac{7}{12}\) = \(\frac{2}{12}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Unlock the Problem

a. What problem are you being asked to solve? Answer: fractions with unequal denominators
b. How will you use the diagram to solve the problem? Answer: By calculating, Number of slices ate by number of slices are not eaten
c. Jason eats 1 of the whole pizza. How many slices does he eat? Answer: \(\frac{1}{8}\)

e. Write a fraction to represent the amount of pizza that is remaining. Answer: \(\frac{5}{8}\)
f. Fill in the bubble for the correct answer choice above. Answer: B
Lesson 5.2 Homework Answer Key 5th Grade Go Math Question 7. H.O.T. Explain how a model for \(\frac{3}{5}\) – \(\frac{1}{2}\) is different from a model for \(\frac{3}{5}\) – \(\frac{3}{10}\). Answer: \(\frac{3}{5}\) – \(\frac{1}{2}\) = \(\frac{6}{10}\) – \(\frac{5}{10}\) = \(\frac{1}{10}\) \(\frac{3}{5}\) – \(\frac{3}{10}\) = \(\frac{6}{10}\) – \(\frac{3}{10}\) = \(\frac{3}{10}\) They both are same subtraction with unequal denominator both get the denominator same with numerator change
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 8. You are making cranberry lemonade for the Tastiest Beverage contest. You use \(\frac{3}{10}\) liter cranberry juice and \(\frac{1}{2}\) liter lemonade. You drink \(\frac{1}{10}\) liter, just to be sure that it tastes delicious! How much cranberry lemonade do you have left? (A) \(\frac{7}{10}\) liter (B) \(\frac{9}{10}\) liter (C) \(\frac{3}{11}\) liter (D) \(\frac{3}{10}\) liter Answer: A \(\frac{3}{10}\) + \(\frac{1}{2}\) = \(\frac{3}{10}\) + \(\frac{5}{10}\) = \(\frac{8}{10}\) \(\frac{8}{10}\) – \(\frac{1}{10}\) =\(\frac{7}{10}\)
Question 9. Use Diagrams Calvin used fraction strips correctly to model the difference of \(\frac{7}{12}\) – \(\frac{1}{3}\). Which of these describes his model? (A) seven \(\frac{1}{12}\) strips, one \(\frac{1}{3}\) strip, two \(\frac{1}{4}\) strips (B) seven \(\frac{1}{12}\) strips, one \(\frac{1}{3}\) strip, one \(\frac{1}{2}\) strip (C) seven \(\frac{1}{12}\) strips, two \(\frac{1}{6}\) strips, one \(\frac{1}{8}\) strip (D) seven \(\frac{1}{12}\) strips, one \(\frac{1}{3}\) strip, one \(\frac{1}{4}\) strip Answer:
Question 10. Multi-Step Bethany made her Apple Surprise drink by mixing \(\frac{1}{8}\) pint lemon juice, \(\frac{1}{8}\) pint grape juice, and \(\frac{4}{8}\) pint apple juice. She then drank \(\frac{1}{4}\) pint of the mixture. How much Apple Surprise was left? (A) \(\frac{1}{2}\) pint (B) \(\frac{1}{8}\) pint (C) \(\frac{1}{4}\) pint (D) \(\frac{3}{8}\) pint Answer: A \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{4}{8}\) = \(\frac{6}{8}\) \(\frac{6}{8}\) – \(\frac{1}{4}\) = \(\frac{6}{8}\) – \(\frac{2}{8}\) = \(\frac{1}{2}\)
Texas Test Prep
Texas Go Math Grade 5 Lesson 5.2 Homework and Practice Answer Key

Question 3. \(\frac{1}{2}\) – \(\frac{1}{3}\) = _____________ Answer: \(\frac{1}{2}\) – \(\frac{1}{3}\) = \(\frac{3}{6}\) – \(\frac{2}{6}\) = \(\frac{1}{6}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 4. \(\frac{9}{10}\) – \(\frac{2}{5}\) = _____________ Answer: \(\frac{9}{10}\) – \(\frac{2}{5}\) = \(\frac{9}{10}\) – \(\frac{4}{10}\) = \(\frac{5}{10}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 5. \(\frac{11}{12}\) – \(\frac{3}{4}\) = _____________ Answer: \(\frac{11}{12}\) – \(\frac{3}{4}\) = \(\frac{11}{12}\) – \(\frac{9}{12}\) =\(\frac{1}{6}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 6. \(\frac{5}{6}\) – \(\frac{1}{3}\) = _____________ Answer: Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 7. \(\frac{2}{3}\) – \(\frac{1}{12}\) = _____________ Answer: Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Go Math Lesson 5.2 Homework Answer Key Grade 5 Question 8. \(\frac{3}{4}\) – \(\frac{5}{12}\) = _____________ Answer: Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 9. \(\frac{9}{10}\) – \(\frac{1}{2}\) = _____________ Answer: Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 10. \(\frac{5}{8}\) – \(\frac{1}{2}\) = _____________ Answer: \(\frac{5}{8}\) – \(\frac{1}{2}\) = \(\frac{5}{8}\) – \(\frac{4}{8}\) = \(\frac{1}{8}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 11. \(\frac{3}{4}\) – \(\frac{2}{3}\) = _____________ Answer: \(\frac{3}{4}\) – \(\frac{2}{3}\) = \(\frac{9}{12}\) – \(\frac{8}{12}\) = \(\frac{1}{12}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Problem Solving
Question 12. Annette is making a fruit drink that calls for \(\frac{3}{4}\) cup of fresh lemon juice. She has \(\frac{1}{2}\) cup of lemon juice. How much more lemon juice does Annette need? Answer: \(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{3}{4}\)–\(\frac{2}{4}\) = \(\frac{1}{4}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Question 13. Ramon needs to walk \(\frac{3}{4}\) mile to the bus stop. He has walked \(\frac{3}{8}\) mile so far. How much farther does Ramon need to walk to get to the bus stop? Answer: \(\frac{3}{4}\) – \(\frac{3}{8}\) = \(\frac{6}{8}\) – \(\frac{3}{8}\) =\(\frac{3}{8}\) Explanation: The fraction with unequal denominators are subtracted to get the sum By doing them to equal denominators
Lesson Check
Fill In the bubble completely to show your answer.
Question 14. Matt spent \(\frac{1}{3}\) of the money in his pocket on a movie ticket. He spent \(\frac{1}{4}\) of the money on a snack. What fraction of his money is left? (A) \(\frac{7}{12}\) (B) \(\frac{5}{12}\) (C) \(\frac{1}{12}\) (D) \(\frac{1}{6}\) Answer: B Explanation: \(\frac{1}{3}\) + \(\frac{1}{4}\) = \(\frac{4}{12}\) + \(\frac{3}{12}\) = \(\frac{7}{12}\) 1 – \(\frac{7}{12}\) = \(\frac{5}{12}\) Matt spent \(\frac{1}{3}\) of the money in his pocket on a movie ticket. He spent \(\frac{1}{4}\) of the money on a snack. \(\frac{5}{12}\) fraction of his money is left.
Go Math Grade 5 Lesson 5.2 Homework Answer Key Question 15. Jabar used fraction strips to model the difference of \(\frac{7}{12}\) –\(\frac{1}{6}\) Which represents the difference? (A) seven \(\frac{1}{12}\) strips (B) one \(\frac{1}{12}\) strip (C) two \(\frac{1}{12}\) strips (D) five \(\frac{1}{12}\) strips Answer: D \(\frac{7}{12}\) – \(\frac{1}{6}\) = \(\frac{7}{12}\) – \(\frac{2}{12}\) = \(\frac{5}{12}\) Explanation: Jabar used fraction strips to model the difference of \(\frac{7}{12}\) –\(\frac{1}{6}\) represents the difference is five \(\frac{1}{12}\) strips
Question 16. Which fraction correctly completes the equation? \(\frac{3}{4}\) – _________ = \(\frac{1}{8}\) (A) \(\frac{7}{8}\) (B) \(\frac{1}{2}\) (C) \(\frac{5}{8}\) (D) \(\frac{1}{4}\) Answer: C Explanation: \(\frac{3}{4}\) – \(\frac{5}{8}\) = \(\frac{1}{8}\)
Question 17. Three friends share a pizza divided into eighths. If each person eats one slice, how many more slices must be eaten so that \(\frac{1}{2}\) of the pizza remains? (A) 1 (B) 2 (C) 3 (D) 4 Answer: A Explanation: Three friends share a pizza divided into eighths.\(\frac{3}{8}\) half of the pizza means 4 pieces If each person eats one slice, 1 more slices must be eaten so that \(\frac{1}{2}\) of the pizza remains
Question 18. Multi-Step Sara and Jon each ordered a medium pizza. Sara ate \(\frac{3}{8}\) of her pizza for lunch and \(\frac{1}{4}\) for a snack. Jon ate \(\frac{1}{2}\) of his pizza for lunch and \(\frac{1}{4}\) for a snack. How much more pizza did Jon eat? (A) \(\frac{1}{8}\) (B) \(\frac{1}{4}\) (C) \(\frac{1}{2}\) (D) \(\frac{1}{3}\) Answer: A Explanation: Sara and Jon each ordered a medium pizza. Sara ate \(\frac{3}{8}\) of her pizza for lunch and \(\frac{1}{4}\) for a snack. \(\frac{3}{8}\) + \(\frac{1}{4}\) = \(\frac{5}{8}\) Jon ate \(\frac{1}{2}\) of his pizza for lunch and \(\frac{1}{4}\) for a snack. \(\frac{1}{2}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\) \(\frac{5}{8}\) – \(\frac{3}{4}\) = \(\frac{1}{8}\) Jon eat \(\frac{1}{8}\)
Question 19. Multi-Step On field day, \(\frac{1}{10}\) of the students in Mrs. Brown’s class competed in jumping events, \(\frac{3}{5}\) of the students competed in running events, and \(\frac{1}{10}\) competed in throwing events. What part of Mrs. Brown’s class did not compete in jumping, running, or throwing events? (A) \(\frac{1}{5}\) (B) \(\frac{7}{10}\) (C) \(\frac{2}{5}\) (D) \(\frac{4}{5}\) Answer: A Explanation: On field day, \(\frac{1}{10}\) of the students in Mrs. Brown’s class competed in jumping events, \(\frac{3}{5}\) of the students competed in running events, and \(\frac{1}{10}\) competed in throwing events. \(\frac{1}{10}\) + \(\frac{3}{5}\) + \(\frac{1}{10}\) = \(\frac{1}{10}\) + \(\frac{6}{10}\) + \(\frac{1}{10}\) = \(\frac{8}{10}\) – 1= \(\frac{1}{5}\)
Share this:
Leave a comment cancel reply.
You must be logged in to post a comment.
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy

Eureka Math Grade 5 Module 2 Lesson 3 Answer Key
Engage ny eureka math 5th grade module 2 lesson 3 answer key, eureka math grade 5 module 2 lesson 3 problem set answer key.
Question 1. Draw a model. Then, write the numerical expressions. a. The sum of 8 and 7, doubled
Answer: The sum of 8 and 7, doubled = 30.

b. 4 times the sum of 14 and 26
Answer: The sum of 14 and 26, 4 times = 160.

c. 3 times the difference between 37.5 and 24.5
Answer: The difference of 37.5 and 24.5, 3 times = 13.0.

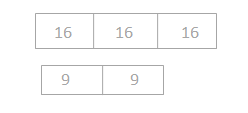
d. The sum of 3 sixteens and 2 nines
Answer: The sum of 3 sixteens and 2 nines = 30.
e. The difference between 4 twenty-fives and 3 twenty-fives
Answer: The difference between 4 25 and 3 25 = 25.
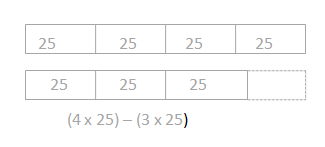
f. Triple the sum of 33 and 27
Answer: The sum of 33 and 27, 3 times = 180.

Question 2. Write the numerical expressions in words. Then, solve.
| Expression | Words | The Value of the Expression |
| a. 12 × (5 + 25) | 12 times the sum of 5 and 25 | 12 x ( 30) = 360 |
| b. (62 – 12) × 11 | 11 times the difference of 62 and 12 | (50) x 11 = 550 |
| c. (45 + 55) × 23 | 23 times the sum of 45 and 55 | (100) x 23 = 2300 |
| d. (30 × 2) + (8 × 2) | product of 30,2 and product of 8,2 | (60) + (16) = 76 |
Answer: 360.
Explanation: In the above-given question, given that, 12 x ( 5 + 25). 12 x (30). 360.
Answer: 550.
Explanation: In the above-given question, given that, (62 – 12) × 11 50 x 11 = 550.
Answer: 2300.
Explanation: In the above-given question, given that, (45 + 55) × 23. 100 x 23. 2300.
Answer: 76.
Explanation: In the above-given question, given that, (30 × 2) + (8 × 2) 60 + 16. 76.
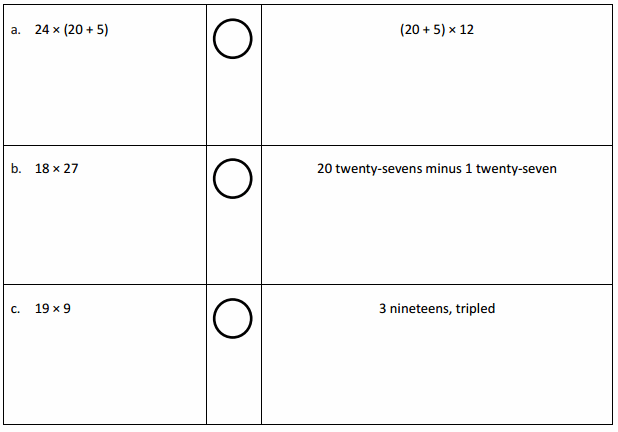
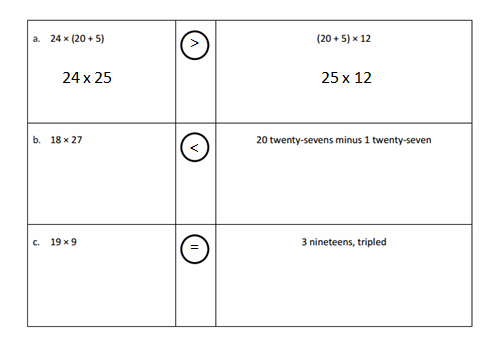
Answer: 600 > 360.
Explanation: In the above-given question, given that, 24 x (20 + 5). 24 x 25. 600. (20 + 5) x 12. 30 x 12. 360. 600 > 360.
Answer: 487 > 513.
Explanation: In the above-given question, given that, 18 x 27. 487. 20 twenty-seven – 1 27. 540 – 27. 513. 487 < 513.
Answer: 171 = 171.
Question 4. Mr. Huynh wrote the sum of 7 fifteens and 38 fifteens on the board. Draw a model, and write the correct expression.
Answer: The sum of 7 fifteens and 38 fifteens = 675.
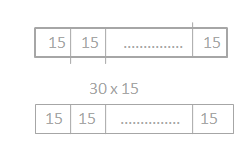
Question 5. Two students wrote the following numerical expressions. Angeline: (7 + 15) × (38 + 15) MeiLing: 15 × (7 + 38) Are the students’ expressions equivalent to your answer in Problem 4? Explain your answer.
Answer: Yes, the student’s expressions equivalent.
Explanation: In the above-given question, given that, Angeline: (7 + 15) × (38 + 15) Meiling: 15 × (7 + 38) 105 + 570 = 675.
Question 6. A box contains 24 oranges. Mr. Lee ordered 8 boxes for his store and 12 boxes for his restaurant. a. Write an expression to show how to find the total number of oranges ordered.
Answer: The total number of oranges ordered= 480.
Explanation: In the above-given question, given that, A box contains 24 oranges. Mr. Lee ordered 8 boxes for his store and 12 boxes for his restaurant. ( 24 x 8 ) + ( 24 x 12) 192 + 288 480
b. Next week, Mr. Lee will double the number of boxes he orders. Write a new expression to represent the number of oranges in next week’s order.
Answer: The total number of oranges ordered= 960.
Explanation: In the above-given question, given that, A box contains 24 oranges. Mr. Lee ordered 8 boxes for his store and 12 boxes for his restaurant. ( 24 x 8 ) + ( 24 x 12) 192 + 288 480 + 480 = 960
c. Evaluate your expression from Part (b) to find the total number of oranges ordered in both weeks.
Answer: The total number of oranges ordered in both weeks = 1440.
Explanation: In the above-given question, given that, 960 + 480 = 1440.
Eureka Math Grade 5 Module 2 Lesson 3 Exit Ticket Answer Key
Question 1. Draw a model. Then, write the numerical expressions. a. The difference between 8 forty-sevens and 7 forty-sevens
Answer: The difference of 8 forty-sevens and 7 forty-sevens = 47.
Explanation: In the above-given question, given that, the difference of 8 forty sevens and 7 forty-sevens. 8 x 47 – 7 x 47. 376 – 329. 47
b. 6 times the sum of 12 and 8
Answer: The sum of 12 and 8, 6 times = 120.
Explanation: In the above-given question, given that, the sum of 12 and 8 is 120. 20 + 20 + 20 + 20 + 20 + 20 = 120. 12 + 8 = 20.

Answer: 4836 > 2028.

Eureka Math Grade 5 Module 2 Lesson 3 Homework Answer Key
Question 1. Draw a model. Then, write the numerical expressions. a. The sum of 21 and 4, doubled b. 5 times the sum of 7 and 23 c. 2 times the difference between 49.5 and 37.5 d. The sum of 3 fifteens and 4 twos e. The difference between 9 thirty-sevens and 8 thirty-sevens f. Triple the sum of 45 and 55
Answer: The sum of 21 and 4, 2 times = 50.

Answer: The sum of 7 and 23, 5 times = 150.

Answer: 2 times the difference between 49.5 and 37.5 = 24.

Answer: The sum of 3 fifteens and 4 twos = 53.
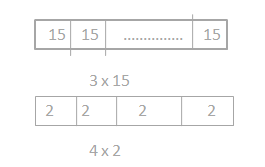
Answer: The difference between 9 thirty-sevens and 8 thirty-sevens = 37.
Explanation: In the above-given question, given that, The difference between 9 thirty-sevens and 8 thirty-sevens 9 x 37 – 8 x 37. 333 – 296. 37.
Triple the sum of 45 and 55 = 300.
Explanation: In the above-given question, given that, Triple the sum of 45 and 55 45 + 55 = 100. 100 + 100 + 100 = 300.
| Expression | Words | The Value of the Expression |
| a. 10 × (2.5 + 13.5) | one hundred and sixty | 10 x (16) = 160 |
| b. (98 – 78) × 11 | two hundred and twenty | (20) x 11 = 220 |
| c. (71 + 29) × 26 | two thousand six hundred | (100) x 26 = 2600 |
| d. (50 × 2) + (15 × 2) | one hundred and thirty | (100) + 30 = 130 |
Answer: 160.
Explanation: In the above-given question, given that, 10 x ( 2.5 + 13.5). 10 x (16). 160.
Answer: 220.
Explanation: In the above-given question, given that, 11 x ( 98 – 78). 11 x (20). 220.
Answer: 2600.
Explanation: In the above-given question, given that, 26 x ( 71 + 29). 26 x (30). 2600.
Answer: 3000.
Explanation: In the above-given question, given that, (50 x 2) + ( 15 + 2). 100 x (30). 3000.
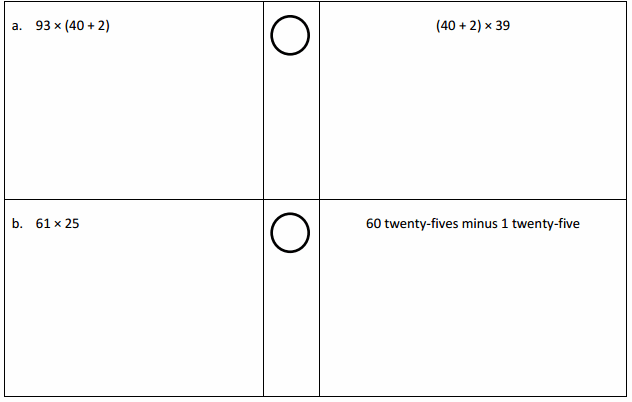
Answer: 3906 > 1438.
Explanation: In the above-given question, given that, 93 x ( 40 + 2). 93 x (42). 3906. (40 + 2) x 36 42 x 36. 1438. 3906 > 1438.
Answer: 1525 > 1475.
Explanation: In the above-given question, given that, 61 x ( 25). 1525. 60 twenty fives minus one twenty-five. 60 x 25 – 25. 1500 – 25. 1475. 1525 > 1475.
Question 4. Larry claims that (14 + 12) × (8 + 12) and (14 × 12) + (8 × 12) are equivalent because they have the same digits and the same operations. a. Is Larry correct? Explain your thinking.
Answer: Yes, Larry was not correct.
Explanation: In the above-given question, given that, Larry claims that (14 + 12) x (8 + 12) and (14 x 12) + (8 x 12). 42 + 12 = 26. 8 + 12 = 20. 26 x 20 = 520. (14 x 12) + (8 x 12). 168 + 96. 264. 520 is not equal to 264.
b. Which expression is greater? How much greater?
Answer: (14 + 12) x (8 + 12) is greater. 256 is greater.
Explanation: In the above-given question, given that, 42 + 12 = 26. 8 + 12 = 20. 26 x 20 = 520. (14 x 12) + (8 x 12). 168 + 96. 264. 520 is not equal to 264.
Leave a Comment Cancel Reply
You must be logged in to post a comment.

IMAGES
VIDEO
COMMENTS
Answer: 3/4 units long 1/2 units wide. Area = 3/8 units 2. Question 5. Colleen and Caroline each built a rectangle out of square tiles placed in 3 rows of 5. Colleen used tiles that measured 1 23 cm in length. Caroline used tiles that measured 3 13 cm in length. a.
2. Solve by drawing the area model and using the standard algorithm. 2,451 × 107 = 262, 257. 3. Solve using the standard algorithm. 7,302 × 408 = 2, 979, 216. 126. Lesson 11: Connect area models and the distributive property to partial products of the standard algorithm with renaming.
0.5 × 5 = 2.5. Answer: 3 x 3 = 9. Explanation: In the above-given question, given that, multiply. 3 x 3 = 9. Question 18. 0.05 × 5 = 025. Answer: 0.05 x 5 = 0.25. ... Eureka Math Grade 5 Module 2 Lesson 11 Homework Answer Key. Question 1. Estimate the product. Solve using the standard algorithm. Use the thought bubbles to show your thinking.
11. 70,000 22. 84,000 33. 867,000 44. 129,000 Side B 1. 80 12. 600,000 23. 37,000 34. ... Lesson 4 Answer Key 5 •2 Lesson 4 Problem Set 1. a. (15 - 1) 29 and (10 29) - (6 29) 4. ... Lesson 4 Answer Key 5 •2 Homework 1. a. (30 19) - (7 29) and (40 - 2) 19 3.
Engage NY // Eureka Math Grade 5 Module 2 Lesson 11 Homework
Multiply decimal fractions by multi digit whole numbers through conversion to a whole number problem and reasoning about the placement of the decimal point, ...
Eureka Math Grade 5 Module 1 Lesson 11 Exit Ticket Answer Key. Question 1. Solve by drawing disks on a place value chart. Write an equation, and express the product in standard form. 4 copies of 3 tenths. Answer:- 4 x 0.3 = 1.2. Question 2. Complete the area model, and then find the product. Answer:- 3 x 9.63 = 28.89.
Special thanks go to the Gordon A. Cain Center and to the Department of Mathematics at Louisiana State University for their support in the development of
Eureka Math Grade 5. Please share this page with your friends on FaceBook. Lesson 1: Homework Answer Keys. Lesson 2: Homework Answer Keys. Lesson 3: Homework Answer Keys. Lesson 4: Homework Answer Keys. Lesson 5: Homework Answer Keys. Lesson 6:Homework Answer Keys. Lesson 7: Homework Answer Keys.
Go Math! Practice Book (TE), G5. Name Divide Decimals bg Whole Numbers use the model to complete the number sentence. 1. 1.2 Divide. use base-ten blocks. 2. Lesson 5.2 COMMON CORE STANDARD CC.5.NBT.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. 1. 3.69 - 3 = lìììììììììì 23.
Lesson 5.2 (Solving Systems of Linear Equations by Substitution) Flashcards; Learn; Test; Match; Q-Chat; Get a hint. solve by substitution: y = 4x and x + y = 5 (1, 4) 1 / 12. 1 / 12. Flashcards; Learn; Test; Match; Q-Chat; Created by. oconnormath Teacher. Share. Find the solution to the system by using substitution.
Exercise 31. Exercise 32. Exercise 33. Exercise 34. At Quizlet, we're giving you the tools you need to take on any subject without having to carry around solutions manuals or printing out PDFs! Now, with expert-verified solutions from Big Ideas Geometry 1st Edition, you'll learn how to solve your toughest homework problems.
Math Expressions Answer Key. Eureka Math Answers. So 1 is carried to the tens place and added to the tens place values. ten place : 1 + 6 + 1 = 8 hundreds place = 3+ 2 = 5 thousands place = 6 + 1 = 7 Sum = 7,582. d. Answer: Explanation: While adding two numbers we add the numbers according to...
Find step-by-step solutions and answers to Precalculus - 9780321900517, as well as thousands of textbooks so you can move forward with confidence. ... Exercise 11. Exercise 12. Exercise 13. Exercise 14. Exercise 15. Exercise 16. Exercise 17. Exercise 18. Exercise 19.
Eureka Math Grade 5 Module 2 Lesson 1 Problem Set Answer Key. Question 1. Fill in the blanks using your knowledge of place value units and basic facts. 23 x 20 = 460. 23 ones x 2 tens = 46 tens. 23 x 20 = 460. 230 x 20 = 4600. 23 tens x 2 tens = 46 tens. 230 x 20 = 4600.
The source for the homework pages is the "full module" PDF, available here for free:https://www.engageny.org/resource/grade-2-mathematics-module-5
McGraw Hill Math Grade 4 Chapter 6 Lesson 7 Answer Key Problem Solving: Extra or Missing Information; McGraw Hill Math Grade 4 Chapter 6 Lesson 6 Answer Key Estimating Quotients; McGraw Hill Math Grade 4 Chapter 6 Lesson 5 Answer Key Using Mental Math to Divide; McGraw Hill Math Grade 4 Chapter 6 Lesson 4 Answer Key Dividing a Four-Digit Number
Engage NY Eureka Math 5th Grade Module 2 Lesson 4 Answer Key Eureka Math Grade 5 Module 2 Lesson 4 Problem Set Answer Key. Question 1. Circle each expression that is not equivalent to the expression in bold. a. 16 × 29. Answer: 16 x 29 = 464. Explanation: In the above-given question, given that, 29 sixteens = 29 x 16. 16 x (30 - 1). 16 x 29 ...
11. 70,000 22. 84,000 33. 867,000 44. 129,000 Side B 1. 80 12. 600,000 23. ... NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 4 Answer Key 5•2 Lesson 4 Problem Set 1. a. (15 - 1) 29 and (10 29) - (6 29) 4. ... NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 4 Answer Key 5•2 Homework 1. a. (30 19) - (7 29) and (40 - 2) 19 3. a. ...
Engage NY Eureka Math 5th Grade Module 6 Lesson 11 Answer Key Eureka Math Grade 5 Module 6 Lesson 11 Sprint Answer Key A Round to the Nearest One Question 1. 3.1 ≈ Answer: 3.1 ... 5 (2, 5) 3: 7 (3, 7) ... Eureka Math Grade 5 Module 6 Lesson 11 Homework Answer Key. Question 1. Complete the tables for the given rules. Line l Rule: Double x. x ...
Exercise 27. Exercise 28. At Quizlet, we're giving you the tools you need to take on any subject without having to carry around solutions manuals or printing out PDFs! Now, with expert-verified solutions from Finite Mathematics 11th Edition, you'll learn how to solve your toughest homework problems. Our resource for Finite Mathematics ...
Eureka Math Grade 5 Module 2 Lesson 3 Homework Answer Key. Question 1. Draw a model. Then, write the numerical expressions. a. The sum of 21 and 4, doubled. b. 5 times the sum of 7 and 23. c. 2 times the difference between 49.5 and 37.5. d.