fractions and decimals problem solving

Solving Problems that Include Fractions and Decimals

Introduction.

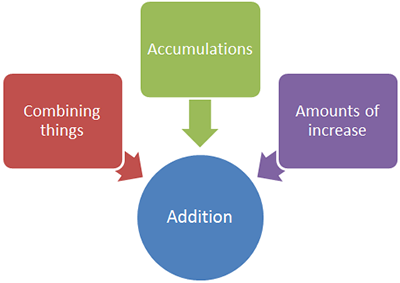
There are four important operations that you will encounter when solving problems in mathematics. The figures below indicate some of the actions in a problem that lead to different operations.

Addition and subtraction are related operations. Addition typically means to combine two or more numbers, and subtraction involves the difference , or removal, of one number from another.

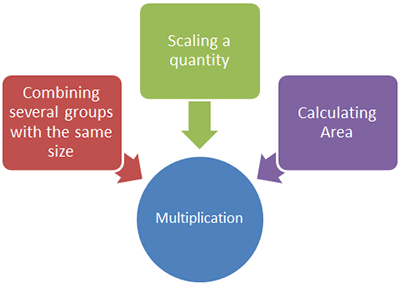
Multiplication and division are also related operations. Both operations involve grouping and rates.

You have explored how to tell when to use which operation. Now, you will focus on identifying the operation from a word problem, and then use procedures to actually perform the operation and determine a solution to the problem.

Working with Signed Numbers

Signed numbers include integers and other rational numbers that have either a positive or a negative sign.

Source: Badwater Elevation Sign, Complex01 and Elevation Benchmark, Jeff Kramer, Wikimedia Commons

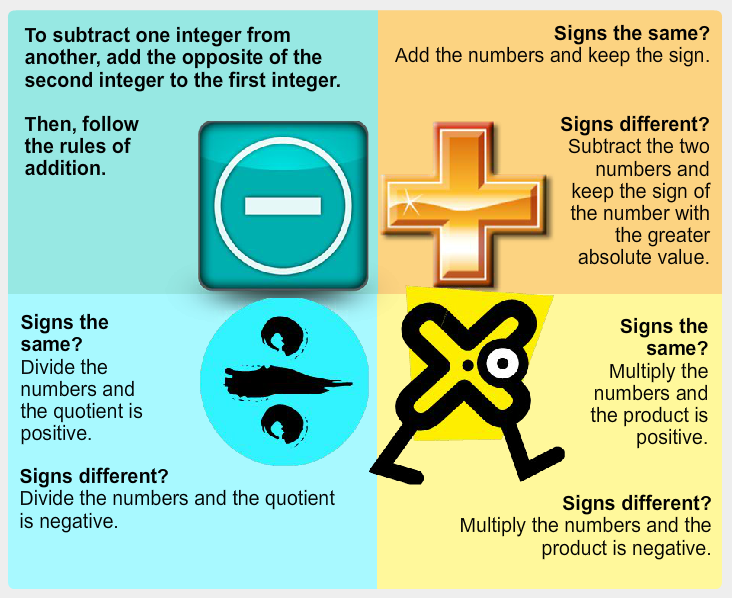
Use the diagram below to review standard procedures for adding, subtracting, multiplying, and dividing integers.

Adding and Subtracting Decimals

You have applied the rules of integers to solve word problems. Now, you will review ways to add and subtract decimals, and then use what you learn to solve problems relating to addition and subtraction of positive and negative decimals.

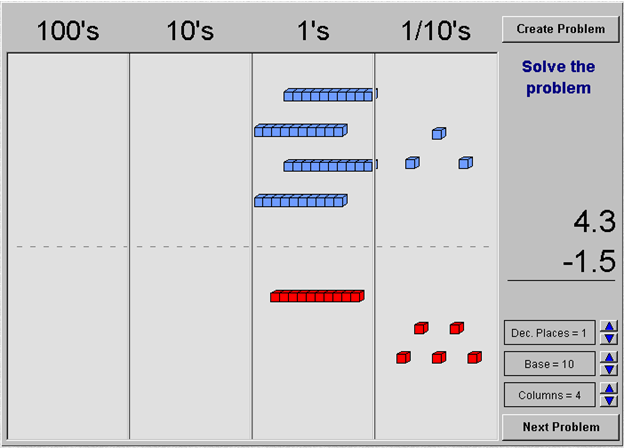
Click on the image below to open a base-ten model interactive in a new web browser tab or window. The interactive represents the two addends in an addition problem, or the minuend  and subtrahend in a subtraction problem. Use the manipulative to work through at least 3 problems.

• Click on a block and drag it on top of its opposite block to remove zero pairs.
• Click on a block and drag it to the next column to regroup.
• Click “Next Problem” to move to the next problem when you are ready.

Need additional help for addition?

Need additional help for subtraction?

Use what you noticed in the interactive to answer the following questions.

In the original problem, 4.3 – 1.5, when you dragged a ones rod into the tenths column, it split into 10 tenths. How does that relate to the regrouping that was recorded symbolically in the image shown below?

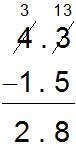
In an addition problem, such as 6.4 + 4.8, when you regroup 10 tenths into 1 one and drag the ones rod into the ones place, how did that action appear in the regrouping that was recorded symbolically such as the regrouping shown in the image below?

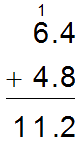
Pause and Reflect

1. Why is it important to line up the decimal point when adding or subtracting decimal numbers?

2. When regrouping 1 one and 3 tenths into 13 tenths, why do you cross out the original 3 in the tenths place and replace it with 13? 

Adding and Subtracting Fractions

You have used models and algorithms to add and subtract decimals, paying special attention to the regrouping that was necessary to perform the computations. Now, you will extend the idea of regrouping to models and procedures used to add and subtract fractions, including mixed numbers.

Consider the following problem.

The example below shows how Marley used fraction strips to solve this problem.

Click the image below to view additional examples, including a video with a worked-out example for you to follow.

1. How is regrouping when subtracting mixed numbers similar to regrouping when subtracting decimals?

2. When adding decimals, you regroup when the sum of the two digits in a place value that is greater than 10. When would you need to regroup as you add mixed numbers?

Multiplying and Dividing Decimals

Now that you’ve investigated addition and subtraction with decimals and fractions, let’s take a closer look at multiplication and division. You will start in this section with decimals, and then use a similar model to multiply and divide fractions and mixed numbers in the next section.

• Write an expression that you can use to determine the amount of oil that Rachel started with.
• How would you represent 2.2 and 2.5 as improper fractions with denominators of 10?

The interactive below uses blocks to multiply decimals. When the blocks are combined, they will form a rectangle; the area of the rectangle is the product of the two decimals or the answer to Rachel’s problem.

• In the first activity, the first decimal is the length of the rectangle, and the second decimal is the width. Represent each decimal by dragging the appropriate blocks and moving them to the area for each decimal.
• In the second activity, use the information from the decimals and drag the blocks to the open area to create a rectangle. You will use the green blocks to fill in the missing pieces of the rectangle.
• Is the answer the same as what we found earlier in Anu's solution?
• Adjust the numerators to create and represent two more multiplication problems. Record those problems on a piece of paper.

Based on what you saw in the interactive, why do you think that the product has the same number of digits to the right of the decimal as the total number of digits to the right of the decimal in the two factors ?

Multiplying and Dividing Fractions

In this section, you will look at models to represent multiplying and dividing fractions.

Multiplying Fractions

Use the interactive below to represent the problem and graphically illustrate the product. Use the Numerator and Denominator sliders to create each fraction or mixed number. You may also need to use the Zoom in/out sliders to see the entire model.

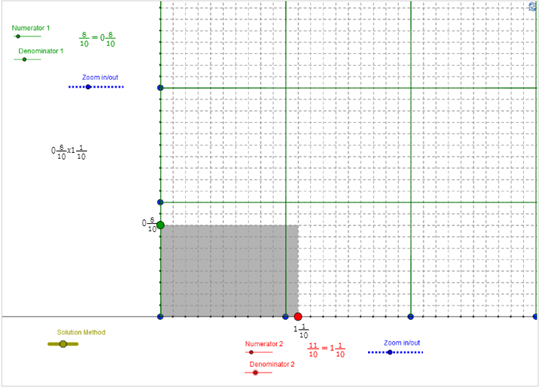
Need additional directions?

Use the interactive to answer the following questions:

• What are the dimensions of the shaded rectangle in the solution? Check Your Answer
• The solid lines represent the boundaries of a rectangle with an area of 1 square unit. The dashed lines represent the boundaries of a number of equal-sized regions within this area. What fraction of 1 does each smaller rectangle represent? Check Your Answer

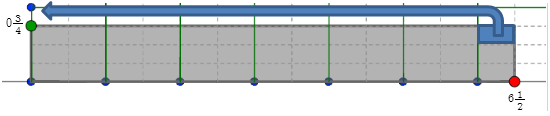
• What mixed number does this rearranged figure represent? How does this compare with the product of 3 4 and 6 1 2 ? Check Your Answer

Dividing Fractions

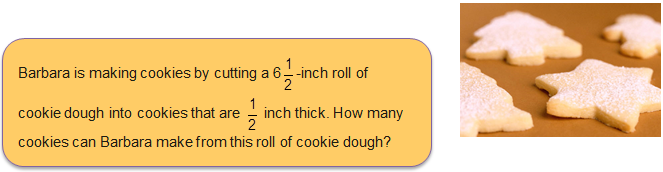
To solve this problem, Barbara used a fraction strip generator, which gave her the following diagram.

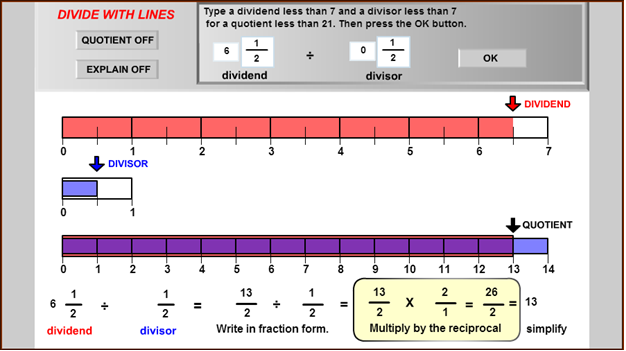
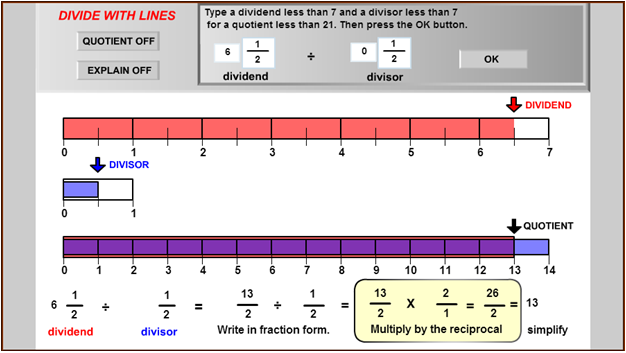
• Barbara knew this was a division problem, not a multiplication problem. How did she know that? Check Your Answer
• Use the diagram to explain why the quotient of 6 1 2 ÷ 1 2 is 13. Check Your Answer

Use the same fraction strip generator that Barbara used to solve the problem below.

Click the image below to open the fraction strip generator in a new web browser tab or window. Enter the key information from the problem, including the dividend and the divisor , and then use the results to answer the questions that follow.

In the fraction diagrams, both 5 3 4 and 3 8 are marked off into eighths. Why do you think that is the case? Check Your Answer

To divide 5 3 4 by 3 8 , the number sentence beneath the diagrams shows multiplication of 5 3 4 by 8 3 , which is the reciprocal of 3 8 . Multiplying by 8 3 is the same as multiplying by 8 , and then dividing by 3 . Why do you need to multiply 5 3 4 by 8 , which is the numerator of the reciprocal? Check Your Answer

The next step in the number sentence divides the product of 5 3 4 and 8 by 3 (multiplies 5 3 4 by the fraction 8 3 ) . Why do you need to divide by 3 at this point? Check Your Answer

See the completed fraction diagram for Patrice's ornament problem.

Completed fraction diagram

1. How does the multiplication algorithm connect to the area model that you used in the first interactive?

2. How does the division algorithm connect to the fraction strip model that you used in the interactive?

You studied models that represent operations on rational numbers (fractions and decimals). You also connected those models to the standard algorithms for performing the operations.

The graphic below summarizes procedures to add, subtract, multiply, and divide decimals.

The graphic below summarizes procedures to add, subtract, multiply, or divide fractions, including mixed numbers.

Copy and paste the link code above.

Related Items

• Unit Conversions
• Sets and Types of Numbers
• Common Multiple and Divisor
• Fractions and Decimals
• Algebraic Expressions and Polynomials
• Equations and Inequalities
• Sequences and Series
• Combinatorics
• Probability and Statistics
• Stereometry
• Analytical Geometry
• Limits, Derivatives, Integrals
• Analysis of Functions
• Trig table and chart

• Link Partners
• Privacy Policy

Copyright © 2015-2023 math-exercises.com - All rights reserved. Any use of website content without written permission is prohibited.

WORD PROBLEMS ON FRACTIONS AND DECIMALS

Problem 1 : 

Each part of a multipart question on a test is worth the same number of points. The whole question is worth 37.5 points. Daniel got 1/2 of the parts of a question correct. How many points did Daniel receive ?

To find the total points received by Daniel, we have to multiply 1/2 and 37.5 

We can solve this word problem using the two methods explained below. 

Method 1 : 

Convert the decimal 3.75 as the fraction 75/2

(1/2) x 37.5  =  (1/2) x (75/2) 

Multiply. Write the product in simplest form.

(1/2) x (75/2)  =  75/4  =  18 ¾

So, Daniel received 18 ¾  points. 

Method 2 : 

Convert the fraction 1/2 as the decimal 0.5

(1/2) x 37.5  =  0.5 x 37.5

Multiply. 

0.5 x 37.5  =  18.75

So, Daniel received 18.75 points. 

Problem 2 : 

The bill for a pizza was $14.50. Charles paid for 3/5 of the bill. How much did he pay ?

To find the amount paid by Charles, we have to multiply 3/5 and 14.50 

Convert the decimal 14.50 as the fraction 29/2

(3/5) x 14.50  =  (3/5) x (29/2) 

(3/5) x (29/2)  =  87/10  =   8 ⁷⁄₁₀

So, Charles paid $ 8 ⁷⁄₁₀ . 

Convert the fraction 3/5 as the decimal 0.6

(3/5) x 14.50  =  0.6 x 14.50

0.6 x 14.50  =  8.7

So, Charles paid $8.7

Problem 3 :

The inner radius of a pipe is 12.625 mm and the outer radius is 18.025 mm. Find the thickness of the pipe.

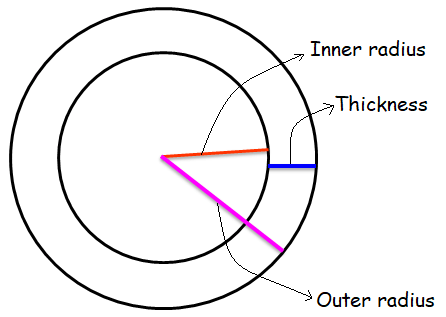
Thickness of the pipe is 

=  Outer radius - Inner radius

=  18.025 - 12.625

=  5.40 mm

Problem 4 :

Jennifer bought 6.5 kg of sugar. she used 3750 grams. How many kilograms of sugar were left ?

3750 grams  =  3750/1000 kg

3750 grams  =  3.75 grams

Amount of sugar left (in kilograms) is 

=  6.5 - 3.75

Problem 5 :

Of the students in the band, 1/4 play the flute and another 1/10 play the clarinet. What fraction of the students in the band play either the flute or the clarinet ?

Fraction of the students in the band play either the flute or the clarinet is 

=  1/4 + 1/10

LCM of (4, 10) is 20. 

So, make each denominator as 20 by multiplying the numerator and denominator of the first fraction by 5 and the second fraction by 2. 

Then we have, 

=  (1 ⋅ 5) / (4 ⋅ 5)  +  (1 ⋅ 2) / (10 ⋅ 2)

=  5/20 + 2/20

=  (5 + 2)/20

=  7/20

So, the fraction of the students who play either the flute or the clarinet is 7/20.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Dec 17, 24 10:13 AM

Digital SAT Math Problems and Solutions (Part - 88)

Dec 17, 24 10:07 AM

Logarithmic Equations Problems and Solutions

Dec 15, 24 08:14 AM

Fractions, Decimals and Percentages Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2025

Advent Calendars 2024 Primary | Secondary

Or search by topic

Number and algebra.

• Properties of numbers
• Place value and the number system
• Calculations and numerical methods
• Fractions, decimals, percentages, ratio and proportion
• Patterns, sequences and structure
• Coordinates, functions and graphs
• Algebraic expressions, equations and formulae

Geometry and measure

• Measuring and calculating with units
• Angles, polygons, and geometrical proof
• 3D geometry, shape and space
• Transformations and constructions
• Pythagoras and trigonometry
• Vectors and matrices

Probability and statistics

• Handling, processing and representing data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets

Advanced mathematics

• Decision mathematics and combinatorics
• Advanced probability and statistics

For younger learners

• Early years foundation stage

Fractions, Decimals and Percentages - Short Problems

This is part of our collection of Short Problems . You may also be interested in our longer problems on Fractions, Decimals and Percentages . Printable worksheets containing selections of these problems are available here .

Ordering fractions

Multiplication magic square

Farthest fraction

Tommy's tankard

Smashing time

Talulah's tulips

Percentage mad

Jacob's flock

Bouncing ball

Information display

Mean sequence

Better spelling

Valuable percentages

Magical products

Three blind mice

Second half score

Smallest fraction

Charlie's money.

Pride of place

Between a sixth and a twelfth.

Too close to call

Peanut harvest

Tricky fractions

Slightly outnumbered

A drink of water

Test scores

Tennis club

The Grand Old Duke of York

What percentage of his 10,000 men did the Grand Old Duke of York have left when he arrived back at the bottom of the hill?

How many rats did the Pied Piper catch?

Entrance exam

Meeting point

Petrol station

2011 digits

Percentage unchanged

Breakfast time

Itchy's fleas

Percentage of a quarter

Percentage swap

Recurring mean

Pineapple juice.

Fractions of 1000

Producing an integer

Squeezed in

Antiques roadshow

Elephants and geese

The property market

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

Common Core - State Standards Initiative

Being able to round and estimate numbers enables people to perform calculations in their head quickly and without using a calculator. Math Games motivates students to practice and hone this important skill by blending learning with play in its appealing online games!

Pupils can use our resources to practice:

• Understanding, identifying and comparing fractions of numbers and shapes
• Making equivalent fractions and reducing fractions
• Performing calculations with fractions and mixed numbers
• Converting between fractions, percents, decimals and mixed numbers

Other resources for teachers and parents include downloadable worksheets and apps, and a digital textbook. We have activities for every grade and ability level, and all of them are aligned with the Common Core State Standards for Mathematics. Choose a skill to start playing!

Home / United States / Math Classes / Worksheets / 6th Grade Fractions, Decimals and Percent Worksheets

6th Grade Fractions, Decimals and Percent Worksheets

The 6th grade fractions, decimals and percent worksheets focus on building up a student’s understanding of writing per cent as fraction and decimal. The problems in these worksheets will enable students to build up their understanding of percentages. ...Read More Read Less

• Interactive Worksheets

Choose Math Worksheets by Grade

Choose math worksheets by topic, 6th grade fractions, decimals and percent worksheets explained.

Percent expresses a number as a part of the number 100 or a part to whole ratio, where the whole is 100. A sound knowledge of percent is essential in a number of real life situations such as percent score in a test or exam, profit or loss percent in a business deal or a transaction, percent share in a business and discount percent offered by a store on a commodity or a service.

The grade 6 fractions, decimals and percent worksheets presents a variety of problems that covers a range of concepts on percent such as:

• Percents and fractions - Students start by understanding the concept of percent and then writing percent as a fraction or a fraction as a percent. The model based interpretation of percent is a useful visual and the sixth grade fractions, decimals and percent worksheets are based on familiarizing students with the conversion of any fraction to a percent using equivalent fractions.
• Percents and decimals - Writing percent as decimals and decimals as a percent is an important skill to solve percent based problems. The 6th grade fractions, decimals and percent worksheets present an array of such problems which strengthens a student’s understanding of how the decimal point moves when multiplying or dividing by 100.
• Comparing and ordering percent - Comparison and ordering of percent values encourages students to have a sound understanding of writing percent in fraction or in decimal form. The fractions, decimals and percent worksheets for grade 6 enable students to compare and order percent, fractions and decimals.

If there is a need to revise specific concepts on percent, go ahead and click on the following links:

• Decimals, percents and fractions
• Percents and fractions
• Ordering and comparing percents, decimals and fractions
• Solving problems based on percent

Benefits of 6th Grade Fractions, Decimals and Percent Worksheets

The grade 6 fractions, decimals and percent worksheets are of great assistance to students in forming a strong foundation on the basics as well as advanced concepts of percent. These worksheets are prepared with varied difficulty levels to allow students to first grasp the fundamentals and then move on to application based problems on percents.

• Fractions, Decimals and Percent Problems-easy 

Sixth grade fractions, decimals and percent worksheets set with an easy difficulty level allow students to start by solving simple and direct questions. Most problems in this worksheet will be based on writing percents as fractions and decimals.

• Fractions, Decimals and Percent Problems-medium

These worksheets for grade 6 enable students to widen their understanding of the concept of fractions, decimals and percents. The problem solving here will require multiple methods or arithmetic operations to make students think from all perspectives. The problems here will be of the type - find the whole if the part and percent is given, or compare and order a set of fractional and decimal numbers.

• Fractions, Decimals and Percent Problems-hard

The harder version of the 6th grade fractions, decimals and percent worksheet caters to problems requiring multi-step estimation of percents or missing values using the concept of percent. The questions in this worksheet also revolve around real life scenarios in which a student will apply the concept of percents to model the situation in equation form or a ratio table.

Printable PDFs and Online Worksheets:

The printable PDF fractions, decimals and percent worksheets for 6th grade can be done offline once downloaded from the website. This will give the students ample scope to solve the worksheet problems without any time limit attached. These PDF worksheets are easy to download and work on. The worksheets with an interactive feature for 6th grade students are solved in an online mode. These worksheets are timed and will encourage the students to participate in such time bound activities in the future. Students are also able to instantly obtain the solutions for these worksheets in the online mode.

How are 6th grade fractions, decimals and percent worksheets beneficial to students?

Regular practice of these grade 6 worksheets boosts active learning among students. Solving these problems instill in them a sense of accomplishment. It raises the curiosity level about percent in relation to specific topics, and in turn, enables them to take up more challenging questions. In these worksheets, students may also learn alternative methods of solving problems and get a deep insight into step-wise solutions that further strengthens their understanding.

Why is it important to have a sound knowledge of fractions and decimals?

In our everyday life we come across many instances where a quantity or an amount includes a whole and a part of the whole or just the part of the whole. In such cases the accurate or precise value of the amount can be expressed in fraction or decimal form.

What is a real-life application of percents?

Problems related to the sale or purchase of an article or service often involve discounts, profits or loss percents. So, students who have a thorough understanding of percent calculations will be able to quickly solve problems related to buying and selling products.

What is the role of grade 6 fractions, decimals and percent worksheets in learning advanced concepts in higher grades?

A sound understanding of the concept of fractions, decimals and percent helps students to quickly learn how to represent part of a whole. A firm understanding of fractions and decimals also comes in handy in percent based problems in higher grades to solve problems on advanced topics such as percent proportion, percent equation, markups, discounts and simple interest.

Do the worksheets on fractions, decimals and percent for grade 6 include word problems?

The problems in these worksheets include questions on finding percent, writing percent as fraction or decimal, determining unknown values in a percent equation and real life scenario-based word problems.

Is there a need to take a subscription to use BYJU’S Math worksheets?

No, a subscription is not required. All worksheets from BYJU’S Math are absolutely free to use.