hypothesis test linear correlation

Module 12: Linear Regression and Correlation

Hypothesis test for correlation, learning outcomes.

• Conduct a linear regression t-test using p-values and critical values and interpret the conclusion in context

The correlation coefficient,  r , tells us about the strength and direction of the linear relationship between x and y . However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient r and the sample size n , together.

We perform a hypothesis test of the “ significance of the correlation coefficient ” to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute  r , the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r , is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is ρ , the Greek letter “rho.”
• ρ = population correlation coefficient (unknown)
• r = sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient  ρ is “close to zero” or “significantly different from zero.” We decide this based on the sample correlation coefficient r and the sample size n .

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is “significant.”

• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.
• What the conclusion means: There is a significant linear relationship between x and y . We can use the regression line to model the linear relationship between x and y in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that the correlation coefficient is “not significant.”

• Conclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is not significantly different from zero.”
• What the conclusion means: There is not a significant linear relationship between x and y . Therefore, we CANNOT use the regression line to model a linear relationship between x and y in the population.
• If r is significant and the scatter plot shows a linear trend, the line can be used to predict the value of y for values of x that are within the domain of observed x values.
• If r is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If r is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed x values in the data.

Performing the Hypothesis Test

• Null Hypothesis: H 0 : ρ = 0
• Alternate Hypothesis: H a : ρ ≠ 0

What the Hypotheses Mean in Words

• Null Hypothesis H 0 : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship (correlation) between x and y in the population.
• Alternate Hypothesis H a : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between x and y in the population.

Drawing a Conclusion

There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the p -value
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%,  α = 0.05

Using the  p -value method, you could choose any appropriate significance level you want; you are not limited to using α = 0.05. But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook).

Method 1: Using a p -value to make a decision

Using the ti-83, 83+, 84, 84+ calculator.

To calculate the  p -value using LinRegTTEST:

• On the LinRegTTEST input screen, on the line prompt for β or ρ , highlight “≠ 0”
• The output screen shows the p-value on the line that reads “p =”.
• (Most computer statistical software can calculate the  p -value).

If the p -value is less than the significance level ( α = 0.05)

• Decision: Reject the null hypothesis.
• Conclusion: “There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.”

If the p -value is NOT less than the significance level ( α = 0.05)

• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero.”

Calculation Notes:

• You will use technology to calculate the p -value. The following describes the calculations to compute the test statistics and the p -value:
• The p -value is calculated using a t -distribution with n – 2 degrees of freedom.
• The formula for the test statistic is [latex]\displaystyle{t}=\dfrac{{{r}\sqrt{{{n}-{2}}}}}{\sqrt{{{1}-{r}^{{2}}}}}[/latex]. The value of the test statistic, t , is shown in the computer or calculator output along with the p -value. The test statistic t has the same sign as the correlation coefficient r .
• The p -value is the combined area in both tails.

Recall: ORDER OF OPERATIONS

1st find the numerator:

Step 1: Find [latex]n-2[/latex], and then take the square root.

Step 2: Multiply the value in Step 1 by [latex]r[/latex].

2nd find the denominator: 

Step 3: Find the square of [latex]r[/latex], which is [latex]r[/latex] multiplied by [latex]r[/latex].

Step 4: Subtract this value from 1, [latex]1 -r^2[/latex].

Step 5: Find the square root of Step 4.

3rd take the numerator and divide by the denominator.

An alternative way to calculate the  p -value (p) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

THIRD-EXAM vs FINAL-EXAM EXAM:  p- value method

• Consider the  third exam/final exam example (example 2).
• The line of best fit is: [latex]\hat{y}[/latex] = -173.51 + 4.83 x  with  r  = 0.6631 and there are  n  = 11 data points.
• Can the regression line be used for prediction?  Given a third exam score ( x  value), can we use the line to predict the final exam score (predicted  y  value)?
• H 0 :  ρ  = 0
• H a :  ρ  ≠ 0
• The  p -value is 0.026 (from LinRegTTest on your calculator or from computer software).
• The  p -value, 0.026, is less than the significance level of  α  = 0.05.
• Decision: Reject the Null Hypothesis  H 0
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Because  r  is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

Method 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of r is significant or not . Compare  r to the appropriate critical value in the table. If r is not between the positive and negative critical values, then the correlation coefficient is significant. If  r is significant, then you may want to use the line for prediction.

Suppose you computed  r = 0.801 using n = 10 data points. df = n – 2 = 10 – 2 = 8. The critical values associated with df = 8 are -0.632 and + 0.632. If r < negative critical value or r > positive critical value, then r is significant. Since r = 0.801 and 0.801 > 0.632, r is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

r is not significant between -0.632 and +0.632. r = 0.801 > +0.632. Therefore, r is significant.

For a given line of best fit, you computed that  r = 0.6501 using n = 12 data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because  r > the positive critical value.

Suppose you computed  r = –0.624 with 14 data points. df = 14 – 2 = 12. The critical values are –0.532 and 0.532. Since –0.624 < –0.532, r is significant and the line can be used for prediction

r = –0.624-0.532. Therefore, r is significant.

For a given line of best fit, you compute that  r = 0.5204 using n = 9 data points, and the critical value is 0.666. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because  r < the positive critical value.

Suppose you computed  r = 0.776 and n = 6. df = 6 – 2 = 4. The critical values are –0.811 and 0.811. Since –0.811 < 0.776 < 0.811, r is not significant, and the line should not be used for prediction.

–0.811 <  r = 0.776 < 0.811. Therefore, r is not significant.

For a given line of best fit, you compute that  r = –0.7204 using n = 8 data points, and the critical value is = 0.707. Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because  r < the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the  third exam/final exam example  again. The line of best fit is: [latex]\hat{y}[/latex] = –173.51+4.83 x  with  r  = 0.6631 and there are  n  = 11 data points. Can the regression line be used for prediction?  Given a third-exam score ( x  value), can we use the line to predict the final exam score (predicted  y  value)?

• Use the “95% Critical Value” table for  r  with  df  =  n  – 2 = 11 – 2 = 9.
• The critical values are –0.602 and +0.602
• Since 0.6631 > 0.602,  r  is significant.

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if  r is significant and the line of best fit associated with each r can be used to predict a y value. If it helps, draw a number line.

• r = –0.567 and the sample size, n , is 19. The df = n – 2 = 17. The critical value is –0.456. –0.567 < –0.456 so r is significant.
• r = 0.708 and the sample size, n , is nine. The df = n – 2 = 7. The critical value is 0.666. 0.708 > 0.666 so r is significant.
• r = 0.134 and the sample size, n , is 14. The df = 14 – 2 = 12. The critical value is 0.532. 0.134 is between –0.532 and 0.532 so r is not significant.
• r = 0 and the sample size, n , is five. No matter what the dfs are, r = 0 is between the two critical values so r is not significant.

For a given line of best fit, you compute that  r = 0 using n = 100 data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between  x and y in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between x and y in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatterplot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

• There is a linear relationship in the population that models the average value of y for varying values of x . In other words, the expected value of y for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population).
• The y values for any particular x value are normally distributed about the line. This implies that there are more y values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of y values lie on the line.
• The standard deviations of the population y values about the line are equal for each value of x . In other words, each of these normal distributions of y  values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

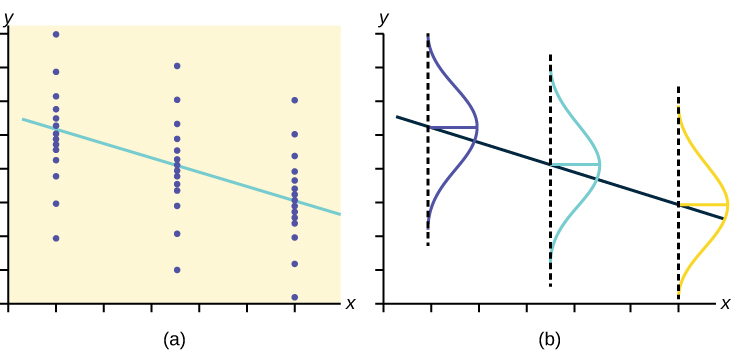
The  y values for each x value are normally distributed about the line with the same standard deviation. For each x value, the mean of the y values lies on the regression line. More y values lie near the line than are scattered further away from the line.

Candela Citations

• Provided by : Lumen Learning. License : CC BY: Attribution
• Testing the Significance of the Correlation Coefficient. Provided by : OpenStax. Located at : https://openstax.org/books/introductory-statistics/pages/12-4-testing-the-significance-of-the-correlation-coefficient . License : CC BY: Attribution . License Terms : Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction
• Introductory Statistics. Authored by : Barbara Illowsky, Susan Dean. Provided by : OpenStax. Located at : https://openstax.org/books/introductory-statistics/pages/1-introduction . License : CC BY: Attribution . License Terms : Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction

Privacy Policy

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Linear Regression and Correlation

Testing the Significance of the Correlation Coefficient

OpenStaxCollege

[latexpage]

The correlation coefficient, r , tells us about the strength and direction of the linear relationship between x and y . However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient r and the sample size n , together.

We perform a hypothesis test of the “significance of the correlation coefficient” to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute r , the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we have only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r , is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is ρ , the Greek letter “rho.”
• ρ = population correlation coefficient (unknown)
• r = sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient ρ is “close to zero” or “significantly different from zero”. We decide this based on the sample correlation coefficient r and the sample size n .

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is “significant.”

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is “not significant”.

• If r is significant and the scatter plot shows a linear trend, the line can be used to predict the value of y for values of x that are within the domain of observed x values.
• If r is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If r is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed x values in the data.

PERFORMING THE HYPOTHESIS TEST

• Null Hypothesis: H 0 : ρ = 0
• Alternate Hypothesis: H a : ρ ≠ 0

WHAT THE HYPOTHESES MEAN IN WORDS:

• Null Hypothesis H 0 : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship(correlation) between x and y in the population.
• Alternate Hypothesis H a : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between x and y in the population.

DRAWING A CONCLUSION: There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the p -value
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%, α = 0.05

Using the p -value method, you could choose any appropriate significance level you want; you are not limited to using α = 0.05. But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook.)

METHOD 1: Using a p -value to make a decision

To calculate the p -value using LinRegTTEST:

On the LinRegTTEST input screen, on the line prompt for β or ρ , highlight “ ≠ 0 “

The output screen shows the p-value on the line that reads “p =”.

• Decision: Reject the null hypothesis.
• Conclusion: “There is sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is significantly different from zero.”
• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: “There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero.”
• You will use technology to calculate the p -value. The following describes the calculations to compute the test statistics and the p -value:
• The p -value is calculated using a t -distribution with n – 2 degrees of freedom.
• The formula for the test statistic is \(t=\frac{r\sqrt{n-2}}{\sqrt{1-{r}^{2}}}\). The value of the test statistic, t , is shown in the computer or calculator output along with the p -value. The test statistic t has the same sign as the correlation coefficient r .
• The p -value is the combined area in both tails.

An alternative way to calculate the p -value (p) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

• Consider the third exam/final exam example .
• The line of best fit is: ŷ = -173.51 + 4.83 x with r = 0.6631 and there are n = 11 data points.
• Can the regression line be used for prediction? Given a third exam score ( x value), can we use the line to predict the final exam score (predicted y value)?
• H 0 : ρ = 0

H a : ρ ≠ 0

• The p -value is 0.026 (from LinRegTTest on your calculator or from computer software).
• The p -value, 0.026, is less than the significance level of α = 0.05.
• Decision: Reject the Null Hypothesis H 0
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Because r is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

METHOD 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of \(r\) is significant or not . Compare r to the appropriate critical value in the table. If r is not between the positive and negative critical values, then the correlation coefficient is significant. If r is significant, then you may want to use the line for prediction.

Suppose you computed r = 0.801 using n = 10 data points. df = n – 2 = 10 – 2 = 8. The critical values associated with df = 8 are -0.632 and + 0.632. If r < negative critical value or r > positive critical value, then r issignificant. Since r = 0.801 and 0.801 > 0.632, r is significant and the line may be usedfor prediction. If you view this example on a number line, it will help you.

For a given line of best fit, you computed that r = 0.6501 using n = 12 data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because r > the positive critical value.

Suppose you computed r = –0.624 with 14 data points. df = 14 – 2 = 12. The critical values are –0.532 and 0.532. Since –0.624 < –0.532, r is significant and the line can be used for prediction

For a given line of best fit, you compute that r = 0.5204 using n = 9 data points, and the critical value is 0.666. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because r < the positive critical value.

Suppose you computed r = 0.776 and n = 6. df = 6 – 2 = 4. The critical values are –0.811 and 0.811. Since –0.811 < 0.776 < 0.811, r is not significant, and the line should not be used for prediction.

For a given line of best fit, you compute that r = –0.7204 using n = 8 data points, and the critical value is = 0.707. Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because r < the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the third exam/final exam example . The line of best fit is: ŷ = –173.51+4.83 x with r = 0.6631 and there are n = 11 data points. Can the regression line be used for prediction? Given a third-exam score ( x value), can we use the line to predict the final exam score (predicted y value)?

• Use the “95% Critical Value” table for r with df = n – 2 = 11 – 2 = 9.
• The critical values are –0.602 and +0.602
• Since 0.6631 > 0.602, r is significant.
• Conclusion:There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ( x ) and the final exam score ( y ) because the correlation coefficient is significantly different from zero.

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if r is significant and the line of best fit associated with each r can be used to predict a y value. If it helps, draw a number line.

• r = –0.567 and the sample size, n , is 19. The df = n – 2 = 17. The critical value is –0.456. –0.567 < –0.456 so r is significant.
• r = 0.708 and the sample size, n , is nine. The df = n – 2 = 7. The critical value is 0.666. 0.708 > 0.666 so r is significant.
• r = 0.134 and the sample size, n , is 14. The df = 14 – 2 = 12. The critical value is 0.532. 0.134 is between –0.532 and 0.532 so r is not significant.
• r = 0 and the sample size, n , is five. No matter what the dfs are, r = 0 is between the two critical values so r is not significant.

For a given line of best fit, you compute that r = 0 using n = 100 data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between x and y in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between x and y in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatterplot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

• There is a linear relationship in the population that models the average value of y for varying values of x . In other words, the expected value of y for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
• The y values for any particular x value are normally distributed about the line. This implies that there are more y values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of y values lie on the line.
• The standard deviations of the population y values about the line are equal for each value of x . In other words, each of these normal distributions of y values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

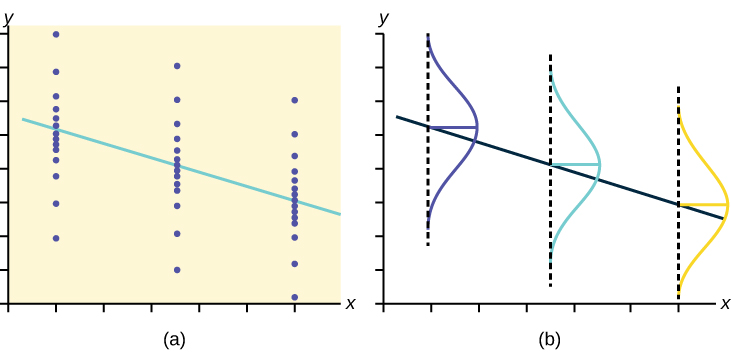
Chapter Review

Linear regression is a procedure for fitting a straight line of the form ŷ = a + bx to data. The conditions for regression are:

• Linear In the population, there is a linear relationship that models the average value of y for different values of x .
• Independent The residuals are assumed to be independent.
• Normal The y values are distributed normally for any value of x .
• Equal variance The standard deviation of the y values is equal for each x value.
• Random The data are produced from a well-designed random sample or randomized experiment.

The slope b and intercept a of the least-squares line estimate the slope β and intercept α of the population (true) regression line. To estimate the population standard deviation of y , σ , use the standard deviation of the residuals, s . \(s=\sqrt{\frac{SEE}{n-2}}\). The variable ρ (rho) is the population correlation coefficient. To test the null hypothesis H 0 : ρ = hypothesized value , use a linear regression t-test. The most common null hypothesis is H 0 : ρ = 0 which indicates there is no linear relationship between x and y in the population. The TI-83, 83+, 84, 84+ calculator function LinRegTTest can perform this test (STATS TESTS LinRegTTest).

Formula Review

Least Squares Line or Line of Best Fit:

\(\stackrel{^}{y}=a+bx\)

a = y -intercept

Standard deviation of the residuals:

\(s=\sqrt{\frac{SEE}{n-2}}.\)

SSE = sum of squared errors

n = the number of data points

When testing the significance of the correlation coefficient, what is the null hypothesis?

When testing the significance of the correlation coefficient, what is the alternative hypothesis?

If the level of significance is 0.05 and the p -value is 0.04, what conclusion can you draw?

If the level of significance is 0.05 and the p -value is 0.06, what conclusion can you draw?

We do not reject the null hypothesis. There is not sufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is not significantly different from zero.

If there are 15 data points in a set of data, what is the number of degree of freedom?

Testing the Significance of the Correlation Coefficient Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Learning Materials

• Business Studies
• Combined Science
• Computer Science
• Engineering
• English Literature
• Environmental Science
• Human Geography
• Macroeconomics
• Microeconomics
• Hypothesis Test for Correlation

Let's look at the hypothesis test for correlation, including the hypothesis test for correlation coefficient, the hypothesis test for negative correlation and the null hypothesis for correlation test.

Millions of flashcards designed to help you ace your studies

Review generated flashcards

to start learning or create your own AI flashcards

Start learning or create your own AI flashcards

StudySmarter Editorial Team

Team Hypothesis Test for Correlation Teachers

• 9 minutes reading time
• Checked by StudySmarter Editorial Team
• Applied Mathematics
• Decision Maths
• Discrete Mathematics
• Logic and Functions
• Mechanics Maths
• Probability and Statistics
• Bayesian Statistics
• Bias in Experiments
• Binomial Distribution
• Binomial Hypothesis Test
• Biostatistics
• Bivariate Data
• Categorical Data Analysis
• Categorical Variables
• Causal Inference
• Central Limit Theorem
• Chi Square Test for Goodness of Fit
• Chi Square Test for Homogeneity
• Chi Square Test for Independence
• Chi-Square Distribution
• Cluster Analysis
• Combining Random Variables
• Comparing Data
• Comparing Two Means Hypothesis Testing
• Conditional Probability
• Conducting A Study
• Conducting a Survey
• Conducting an Experiment
• Confidence Interval for Population Mean
• Confidence Interval for Population Proportion
• Confidence Interval for Slope of Regression Line
• Confidence Interval for the Difference of Two Means
• Confidence Intervals
• Correlation Math
• Cox Regression
• Cumulative Distribution Function
• Cumulative Frequency
• Data Analysis
• Data Interpretation
• Decision Theory
• Degrees of Freedom
• Discrete Random Variable
• Discriminant Analysis
• Distributions
• Empirical Bayes Methods
• Empirical Rule
• Errors In Hypothesis Testing
• Estimation Theory
• Estimator Bias
• Events (Probability)
• Experimental Design
• Factor Analysis
• Frequency Polygons
• Generalization and Conclusions
• Geometric Distribution
• Geostatistics
• Hierarchical Modeling
• Hypothesis Test for Regression Slope
• Hypothesis Test of Two Population Proportions
• Hypothesis Testing
• Inference For Distributions Of Categorical Data
• Inferences in Statistics
• Item Response Theory
• Kaplan-Meier Estimate
• Kernel Density Estimation
• Large Data Set
• Lasso Regression
• Latent Variable Models
• Least Squares Linear Regression
• Linear Interpolation
• Linear Regression
• Logistic Regression
• Machine Learning
• Mann-Whitney Test
• Markov Chains
• Mean and Variance of Poisson Distributions
• Measures of Central Tendency
• Methods of Data Collection
• Mixed Models
• Multilevel Modeling
• Multivariate Analysis
• Neyman-Pearson Lemma
• Non-parametric Methods
• Normal Distribution
• Normal Distribution Hypothesis Test
• Normal Distribution Percentile
• Ordinal Regression
• Paired T-Test
• Parametric Methods
• Path Analysis
• Point Estimation
• Poisson Regression
• Principle Components Analysis
• Probability
• Probability Calculations
• Probability Density Function
• Probability Distribution
• Probability Generating Function
• Product Moment Correlation Coefficient
• Quantile Regression
• Quantitative Variables
• Random Effects Model
• Random Variables
• Randomized Block Design
• Regression Analysis
• Residual Sum of Squares
• Robust Statistics
• Sample Mean
• Sample Proportion
• Sampling Distribution
• Sampling Theory
• Scatter Graphs
• Sequential Analysis
• Single Variable Data
• Spearman's Rank Correlation
• Spearman's Rank Correlation Coefficient
• Standard Deviation
• Standard Error
• Standard Normal Distribution
• Statistical Graphs
• Statistical Inference
• Statistical Measures
• Stem and Leaf Graph
• Stochastic Processes
• Structural Equation Modeling
• Sum of Independent Random Variables
• Survey Bias
• Survival Analysis
• Survivor Function
• T-distribution
• The Power Function
• Time Series Analysis
• Transforming Random Variables
• Tree Diagram
• Two Categorical Variables
• Two Quantitative Variables
• Type I Error
• Type II Error
• Types of Data in Statistics
• Variance for Binomial Distribution
• Venn Diagrams
• Wilcoxon Test
• Zero-Inflated Models
• Theoretical and Mathematical Physics

Jump to a key chapter

What is the hypothesis test for correlation coefficient?

When given a sample of bivariate data (data which include two variables), it is possible to calculate how linearly correlated the data are, using a correlation coefficient.

The product moment correlation coefficient (PMCC) describes the extent to which one variable correlates with another. In other words, the strength of the correlation between two variables. The PMCC for a sample of data is denoted by r , while the PMCC for a population is denoted by ρ.

The PMCC is limited to values between -1 and 1 (included).

If r = 1 , there is a perfect positive linear correlation. All points lie on a straight line with a positive gradient, and the higher one of the variables is, the higher the other.

If r = 0 , there is no linear correlation between the variables.

If r = - 1 , there is a perfect negative linear correlation. All points lie on a straight line with a negative gradient, and the higher one of the variables is, the lower the other.

Correlation is not equivalent to causation, but a PMCC close to 1 or -1 can indicate that there is a higher likelihood that two variables are related.

The PMCC should be able to be calculated using a graphics calculator by finding the regression line of y on x, and hence finding r (this value is automatically calculated by the calculator), or by using the formula r = S x y S x x S y y , which is in the formula booklet. The closer r is to 1 or -1, the stronger the correlation between the variables, and hence the more closely associated the variables are. You need to be able to carry out hypothesis tests on a sample of bivariate data to determine if we can establish a linear relationship for an entire population. By calculating the PMCC, and comparing it to a critical value, it is possible to determine the likelihood of a linear relationship existing.

What is the hypothesis test for negative correlation?

To conduct a hypothesis test, a number of keywords must be understood:

Null hypothesis ( H 0 ) : the hypothesis assumed to be correct until proven otherwise

Alternative hypothesis ( H 1 ) : the conclusion made if H 0 is rejected.

Hypothesis test: a mathematical procedure to examine a value of a population parameter proposed by the null hypothesis compared to the alternative hypothesis.

Test statistic: is calculated from the sample and tested in cumulative probability tables or with the normal distribution as the last part of the significance test.

Critical region: the range of values that lead to the rejection of the null hypothesis.

Significance level: the actual significance level is the probability of rejecting H 0 when it is in fact true.

The null hypothesis is also known as the 'working hypothesis'. It is what we assume to be true for the purpose of the test, or until proven otherwise.

The alternative hypothesis is what is concluded if the null hypothesis is rejected. It also determines whether the test is one-tailed or two-tailed.

A one-tailed test allows for the possibility of an effect in one direction, while two-tailed tests allow for the possibility of an effect in two directions, in other words, both in the positive and the negative directions. Method: A series of steps must be followed to determine the existence of a linear relationship between 2 variables. 1 . Write down the null and alternative hypotheses ( H 0 a n d H 1 ). The null hypothesis is always ρ = 0 , while the alternative hypothesis depends on what is asked in the question. Both hypotheses must be stated in symbols only (not in words).

2 . Using a calculator, work out the value of the PMCC of the sample data, r .

3 . Use the significance level and sample size to figure out the critical value. This can be found in the PMCC table in the formula booklet.

4 . Take the absolute value of the PMCC and r , and compare these to the critical value. If the absolute value is greater than the critical value, the null hypothesis should be rejected. Otherwise, the null hypothesis should be accepted.

5 . Write a full conclusion in the context of the question. The conclusion should be stated in full: both in statistical language and in words reflecting the context of the question. A negative correlation signifies that the alternative hypothesis is rejected: the lack of one variable correlates with a stronger presence of the other variable, whereas, when there is a positive correlation, the presence of one variable correlates with the presence of the other.

How to interpret results based on the null hypothesis

From the observed results (test statistic), a decision must be made, determining whether to reject the null hypothesis or not.

Both the one-tailed and two-tailed tests are shown at the 5% level of significance. However, the 5% is distributed in both the positive and negative side in the two-tailed test, and solely on the positive side in the one-tailed test.

From the null hypothesis, the result could lie anywhere on the graph. If the observed result lies in the shaded area, the test statistic is significant at 5%, in other words, we reject H 0 . Therefore, H 0 could actually be true but it is still rejected. Hence, the significance level, 5%, is the probability that H 0 is rejected even though it is true, in other words, the probability that H 0 is incorrectly rejected. When H 0 is rejected, H 1 (the alternative hypothesis) is used to write the conclusion.

We can define the null and alternative hypotheses for one-tailed and two-tailed tests:

For a one-tailed test:

• H 0 : ρ = 0 : H 1 ρ > 0 o r
• H 0 : ρ = 0 : H 1 ρ < 0

For a two-tailed test:

• H 0 : ρ = 0 : H 1 ρ ≠ 0

Let us look at an example of testing for correlation.

12 students sat two biology tests: one was theoretical and the other was practical. The results are shown in the table.

a) Find the product moment correlation coefficient for this data, to 3 significant figures.

b) A teacher claims that students who do well in the theoretical test tend to do well in the practical test. Test this claim at the 0.05 level of significance, clearly stating your hypotheses.

a) Using a calculator, we find the PMCC (enter the data into two lists and calculate the regression line. the PMCC will appear). r = 0.935 to 3 sign. figures

b) We are testing for a positive correlation, since the claim is that a higher score in the theoretical test is associated with a higher score in the practical test. We will now use the five steps we previously looked at.

1. State the null and alternative hypotheses. H 0 : ρ = 0 and H 1 : ρ > 0

2. Calculate the PMCC. From part a), r = 0.935

3. Figure out the critical value from the sample size and significance level. The sample size, n , is 12. The significance level is 5%. The hypothesis is one-tailed since we are only testing for positive correlation. Using the table from the formula booklet, the critical value is shown to be cv = 0.4973

4. The absolute value of the PMCC is 0.935, which is larger than 0.4973. Since the PMCC is larger than the critical value at the 5% level of significance, we can reach a conclusion.

5. Since the PMCC is larger than the critical value, we choose to reject the null hypothesis. We can conclude that there is significant evidence to support the claim that students who do well in the theoretical biology test also tend to do well in the practical biology test.

Let us look at a second example.

A tetrahedral die (four faces) is rolled 40 times and 6 'ones' are observed. Is there any evidence at the 10% level that the probability of a score of 1 is less than a quarter?

The expected mean is 10 = 40 × 1 4 . The question asks whether the observed result (test statistic 6 is unusually low.

We now follow the same series of steps.

1. State the null and alternative hypotheses. H 0 : ρ = 0 and H 1 : ρ <0.25

2. We cannot calculate the PMCC since we are only given data for the frequency of 'ones'.

3. A one-tailed test is required ( ρ < 0.25) at the 10% significance level. We can convert this to a binomial distribution in which X is the number of 'ones' so X ~ B ( 40 , 0 . 25 ) , we then use the cumulative binomial tables. The observed value is X = 6. To P ( X ≤ 6 ' o n e s ' i n 40 r o l l s ) = 0 . 0962 .

4. Since 0.0962, or 9.62% <10%, the observed result lies in the critical region.

5. We reject and accept the alternative hypothesis. We conclude that there is evidence to show that the probability of rolling a 'one' is less than 1 4

Hypothesis Test for Correlation - Key takeaways

• The Product Moment Correlation Coefficient (PMCC), or r , is a measure of how strongly related 2 variables are. It ranges between -1 and 1, indicating the strength of a correlation.
• The closer r is to 1 or -1 the stronger the (positive or negative) correlation between two variables.
• The null hypothesis is the hypothesis that is assumed to be correct until proven otherwise. It states that there is no correlation between the variables.
• The alternative hypothesis is that which is accepted when the null hypothesis is rejected. It can be either one-tailed (looking at one outcome) or two-tailed (looking at both outcomes – positive and negative).
• If the significance level is 5%, this means that there is a 5% chance that the null hypothesis is incorrectly rejected.

Images One-tailed test: https://en.wikipedia.org/w/index.php?curid=35569621

Learn faster with the 0 flashcards about Hypothesis Test for Correlation

Sign up for free to gain access to all our flashcards.

Already have an account? Log in

Frequently Asked Questions about Hypothesis Test for Correlation

Is the Pearson correlation a hypothesis test?

Yes. The Pearson correlation produces a PMCC value, or r   value, which indicates the strength of the relationship between two variables.

Can we test a hypothesis with correlation?

Yes. Correlation is not equivalent to causation, however we can test hypotheses to determine whether a correlation (or association) exists between two variables.

How do you set up the hypothesis test for correlation?

You need a null (p = 0) and alternative hypothesis. The PMCC, or r value must be calculated, based on the sample data. Based on the significance level and sample size, the critical value can be worked out from a table of values in the formula booklet. Finally the r value and critical value can be compared to determine which hypothesis is accepted.

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter is a globally recognized educational technology company, offering a holistic learning platform designed for students of all ages and educational levels. Our platform provides learning support for a wide range of subjects, including STEM, Social Sciences, and Languages and also helps students to successfully master various tests and exams worldwide, such as GCSE, A Level, SAT, ACT, Abitur, and more. We offer an extensive library of learning materials, including interactive flashcards, comprehensive textbook solutions, and detailed explanations. The cutting-edge technology and tools we provide help students create their own learning materials. StudySmarter’s content is not only expert-verified but also regularly updated to ensure accuracy and relevance.

Team Math Teachers

Study anywhere. Anytime.Across all devices.

Create a free account to save this explanation..

Save explanations to your personalised space and access them anytime, anywhere!

By signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.

Sign up to highlight and take notes. It’s 100% free.

Join over 22 million students in learning with our StudySmarter App

The first learning app that truly has everything you need to ace your exams in one place

• Flashcards & Quizzes
• AI Study Assistant
• Study Planner
• Smart Note-Taking

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

9.4.1 - hypothesis testing for the population correlation.

In this section, we present the test for the population correlation using a test statistic based on the sample correlation.

As with all hypothesis test, there are underlying assumptions. The assumptions for the test for correlation are:

• The are no outliers in either of the two quantitative variables.
• The two variables should follow a normal distribution

If there is no linear relationship in the population, then the population correlation would be equal to zero.

\(H_0\colon \rho=0\) (\(X\) and \(Y\) are linearly independent, or X and Y have no linear relationship)

\(H_a\colon \rho\ne0\) (\(X\) and \(Y\) are linearly dependent)

Under the null hypothesis and with above assumptions, the test statistic, \(t^*\), found by:

\(t^*=\dfrac{r\sqrt{n-2}}{\sqrt{1-r^2}}\)

which follows a \(t\)-distribution with \(n-2\) degrees of freedom.

As mentioned before, we will use Minitab for the calculations. The output from Minitab previously used to find the sample correlation also provides a p-value. This p-value is for the two-sided test. If the alternative is one-sided, the p-value from the output needs to be adjusted.

Example 9-7: Student height and weight (Tests for \(\rho\)) Section  

For the height and weight example ( university_ht_wt.TXT ), conduct a test for correlation with a significance level of 5%.

The output from Minitab is:

Correlation: height, weight

Correlations.

For the sake of this example, we will find the test statistic and the p-value rather than just using the Minitab output. There are 28 observations.

The test statistic is:

\begin{align} t^*&=\dfrac{r\sqrt{n-2}}{\sqrt{1-r^2}}\\&=\dfrac{(0.711)\sqrt{28-2}}{\sqrt{1-0.711^2}}\\&=5.1556 \end{align}

Next, we need to find the p-value. The p-value for the two-sided test is:

\(\text{p-value}=2P(T>5.1556)<0.0001\)

Therefore, for any reasonable \(\alpha\) level, we can reject the hypothesis that the population correlation coefficient is 0 and conclude that it is nonzero. There is evidence at the 5% level that Height and Weight are linearly dependent.

Try it! Section  

For the sales and advertising example, conduct a test for correlation with a significance level of 5% with Minitab.

Sales units are in thousands of dollars, and advertising units are in hundreds of dollars.

Correlation: Y,X

The sample correlation is 0.904. This value indicates a strong positive linear relationship between sales and advertising.

For the Sales (Y) and Advertising (X) data, the test statistic is...

\(t^*=\dfrac{(0.904)\sqrt{5-2}}{\sqrt{1-(0.904)^2}}=3.66\)

...with df of 3, we arrive at a p -value = 0.035. For \(\alpha=0.05\), we can reject the hypothesis that the population correlation coefficient is 0 and conclude that it is nonzero, i.e., conclude that sales and advertising are linearly dependent.